白云一片去悠悠

问题:
给定一个\(n\times m\)的矩阵，给定的方式为给定一个长度为\(n\)的数组\(a\)和一个长度为\(m\)的数组\(b\)，矩阵中的权值\(w_{i,j}=a_i+b_j\)，再给定一个正整数\(x\)，问权值小于等于\(x\)的点能组成多少四连通块。
思路:
首先解决四联通块计数问题有一个\(trick\)，就是可以用四连通块中的一个点代表这个四连通块，这个问题中我们可以用权值最小的点代替，如果有多个最小就去左上角的那个。但是不会有多个左上角吗？
如:

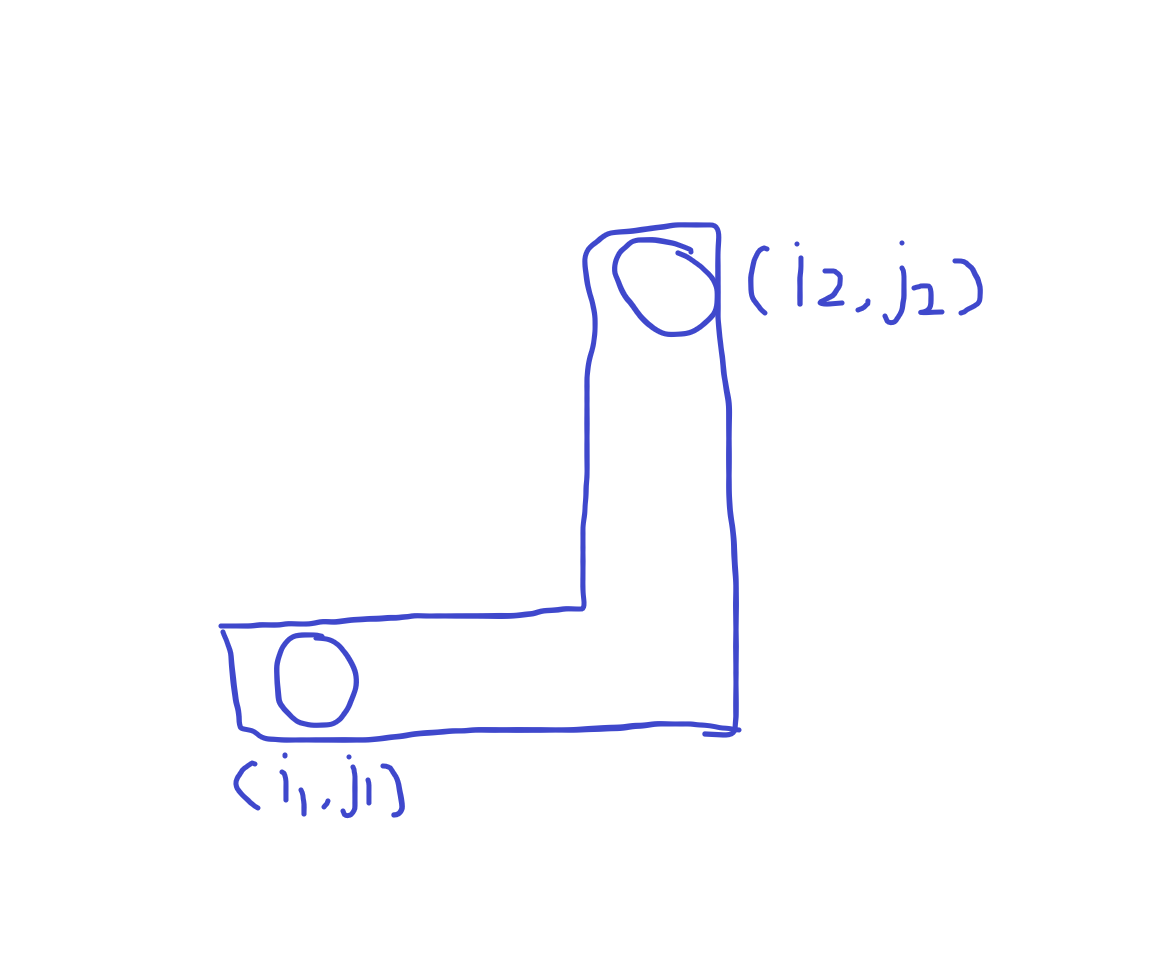
其满足
\(\left\{\begin{matrix} a_{i_1}+b_{j_1}=a_{i_2}+b_{j_2}\\ a_{i_1}+b_{j_2}>a_{i_1}+b_{j_1}\\a_{i_2}+b_{j_1}>a_{i_1}+b_{j_1}\end{matrix}\right.\)
矛盾，所以这种情况不成立。
这样我只需要找出可作为代表点的个数就可以了。
要成为代表点首先要满足\(a_i+b_j\le x\)，并且要满足如下图:

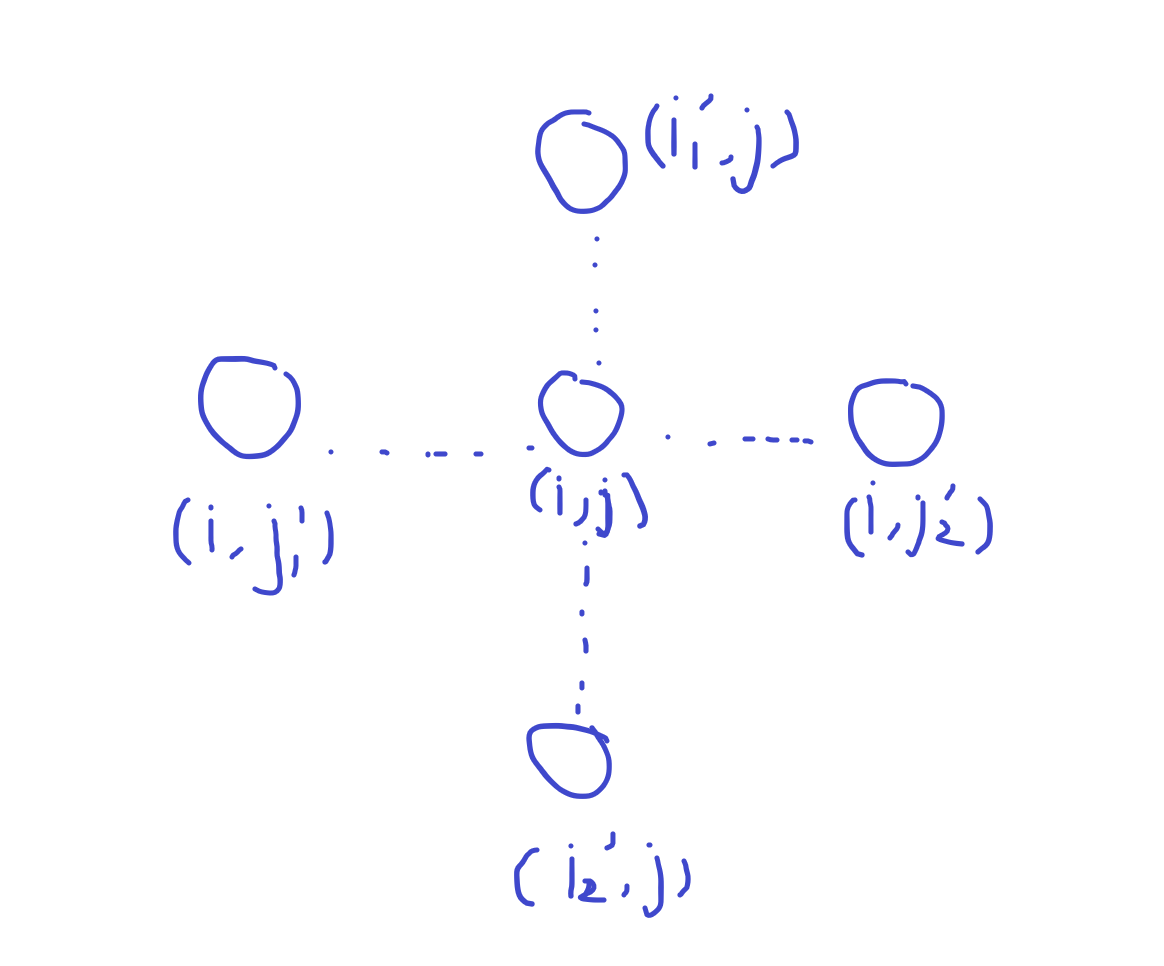
\((i,j_{1}^{`})\)和\((i_{1}^{`},j)\)是\((i,j)\)的向左和向上的最近权值小于等于\((i,j)\)的点。
\((i,j_{2}^{`})\)和\((i_{2}^{`},j)\)是\((i,j)\)的向右和向下的最近权值小于\((i,j)\)的点。
要使\((i,j)\)为代表点必须不能让它与这四个点联通，即定义一个\(f\)数组，\(f_i=\min(\max(a_{i_{1}^{`}+1\sim i-1}),\max(a_{i+1\sim i_{2}^{`}-1}))\)，以及一个\(g\)数组，\(g_j=\min(\max(b_{j_{1}^{`}+1\sim j-1}),\max(b_{j+1\sim j_{2}^{`}-1}))\)，要满足
\(\left\{\begin{matrix} a_i+g_j>x\\f_i+b_j>x \end{matrix}\right.\)
所以总的来说需要满足三个条件：
\(\left\{\begin{matrix}a_i+g_j>x \\ f_i+b_j>x\\ a_i+b_j\le x\end{matrix}\right.\)
最后让\(a\)数组单调，且用主席树维护\(f\)数组，就可以做出。
代码:

#include<iostream>
#include<algorithm>
#include<cstdio>
#define INF 200010
using namespace std;
int kd(){
	int x=0,f=1;
	char a=getchar();
	while(a<'0'||a>'9'){
		if(a=='-'){
			f=-1;
		}
		a=getchar();
	}
	while(a>='0'&&a<='9'){
		x=x*10+a-'0';
		a=getchar();
	}
	return x*f;
}
int n,m,x;
struct node{
	int zhi;
	int f;
}a[200010],b[200010];
bool cmp(node x,node y){
	return x.zhi<y.zhi;
}
int zhan[200010],top;
struct nod{
	int l,r;
	int ls,rs;
	int sum;
}tree[6000010];
int cnt=0;
int tou[200010];
void build(int i,int l,int r){
	tree[i].l=l;
	tree[i].r=r;
	tree[i].sum=0;
	if(l==r){
		return ;
	}
	int mid=(l+r)/2;
	tree[i].ls=++cnt;
	build(cnt,l,mid);
	tree[i].rs=++cnt;
	build(cnt,mid+1,r);
}
void buil(int i,int j,int p){
	tree[i].sum++;
	if(tree[i].l==tree[i].r){
		return ;
	}
	if(tree[tree[i].ls].r>=p){
		tree[i].ls=++cnt;
		tree[cnt]=tree[tree[j].ls];
		buil(cnt,tree[j].ls,p);
	}
	else{
		tree[i].rs=++cnt;
		tree[cnt]=tree[tree[j].rs];
		buil(cnt,tree[j].rs,p);
	}
}
int search(int i,int j,int l,int r){
	if(tree[i].l>=l&&tree[i].r<=r){
		return tree[i].sum-tree[j].sum;
	}
	int s=0;
	if(tree[tree[i].ls].r>=l){
		s+=search(tree[i].ls,tree[j].ls,l,r);
	}
	if(tree[tree[i].rs].l<=r){
		s+=search(tree[i].rs,tree[j].rs,l,r);
	}
	return s;
}
long long ans;
int main(){
	cin>>n>>m>>x;
	for(int i=1;i<=n;i++){
		a[i].zhi=kd();
	}
	top=0;
	for(int i=1;i<=n;i++){
		int maxn=0;
		while(top>0&&a[zhan[top]].zhi>a[i].zhi){
			int cun=a[zhan[top]].f;
			a[zhan[top]].f=min(a[zhan[top]].f,maxn);
			maxn=max(maxn,max(cun,a[zhan[top]].zhi));
			top--;
		}
		if(top==0){
			maxn=INF;
		}
		a[i].f=maxn;
		zhan[++top]=i;
	}
	for(int i=1;i<=m;i++){
		b[i].zhi=kd();
	}
	top=0;
	for(int i=1;i<=m;i++){
		int maxn=0;
		while(top>0&&b[zhan[top]].zhi>b[i].zhi){
			int cun=b[zhan[top]].f;
			b[zhan[top]].f=min(b[zhan[top]].f,maxn);
			maxn=max(maxn,max(cun,b[zhan[top]].zhi));
			top--;
		}
		if(top==0){
			maxn=INF;
		}
		b[i].f=maxn;
		zhan[++top]=i;
	}
	sort(a+1,a+n+1,cmp);
	tou[0]=++cnt;
	build(1,1,200000);
	for(int i=1;i<=n;i++){
		tou[i]=++cnt;
		tree[cnt]=tree[tou[i-1]];
		buil(tou[i],tou[i-1],a[i].f);
	}
	for(int i=1;i<=m;i++){
		int l=1,r=n;
		while(l<r){
			int mid=(l+r)/2;
			if(a[mid].zhi+b[i].f>x){
				r=mid;
			} 
			else{
				l=mid+1;
			}
		}
		int ll=l;
		if(a[n].zhi+b[i].f<=x){
			ll=n+1;
		}
		l=1,r=n;
		while(l<r){
			int mid=(l+r+1)/2;
			if(a[mid].zhi+b[i].zhi<=x){
				l=mid;
			}
			else{
				r=mid-1;
			}
		}
		int rr=l;
		if(a[1].zhi+b[i].zhi>x){
			rr=0;
		}
		if(ll<=rr){
			ans+=search(tou[rr],tou[ll-1],max(x-b[i].zhi+1,1),200000);
		}
	}
	cout<<ans;
	return 0;
}