卡特兰数
卡特兰数:$C(n)=\binom{2n}{n}-\binom{2n}{n+1}=\frac{\binom{2n}{n}}{n+1} $
几何表示:
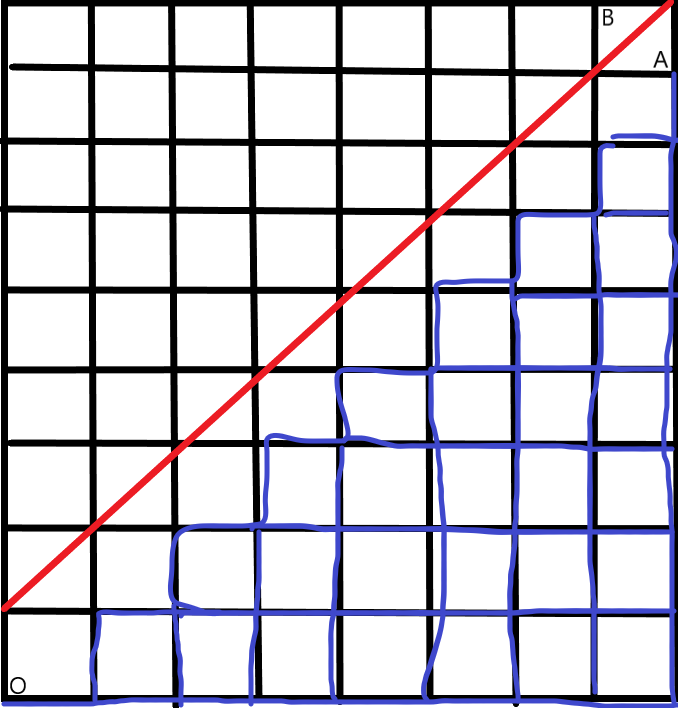
卡特兰数表示从点O到点A,只能向上或向右走蓝色线段的方案数,即从点O到点A,只能向上或向右走的方案数减去从点O到点A,向上或向右走经过红线的方案数。
从点O到点A,只能向上或向右走的方案数是\(\binom{2n}{n}\)。
从点O到点A,向上或向右走经过红线的方案数是从点O到点B,向上或向右走的方案数是\(\binom{2n}{n+1}\)。
推出卡特兰数:$C(n)=\binom{2n}{n}-\binom{2n}{n+1}=\frac{\binom{2n}{n}}{n+1} $。
例题:
洛谷P3200
思路:
我们会发现当在2位置放m,则\(1~m-1\)的位置就会确定,是依次在奇数位放置,接着放下一个偶数位,也是一样的,就有状态\(f[i][j]\)表示在第i个位置放j的方案数,转移方程\(f[i][j]=\sum_{k=i-2}^{n+\frac{i}{2}} f[i-2][k]\)优化得\(f[i][j]=f[i-2][j-1]+f[i][j-1] (i-1\le j\le n+\frac{i}{2})\) 是卡特兰数。但是p不一定是质数,不能用逆元,可以看每个质因数在其中出现几次,我们可以求出质因数i在\(n!\)中的个数就是$\sum_{k=1}^{\infty} \left \lfloor \frac{n}{i^{k}}\right \rfloor $,那么就可以算了。
代码:
#include<iostream>
using namespace std;
int n,p;
int ss[2000010];
bool prime[2000010];
long long ksm(long long x,long long y){
if(y==0){
return 1;
}
long long ans=ksm(x,y/2);
ans=ans*ans%p;
if(y%2==1){
ans=ans*x%p;
}
return ans;
}
long long ans=1;
int main(){
cin>>n>>p;
for(int i=2;i<=2*n;i++){
if(prime[i]==0){
long long cnt=0;
int m=2*n;
while(m){
cnt+=m/i;
m/=i;
}
m=n;
while(m){
cnt-=m/i;
m/=i;
}
m=n+1;
while(m){
cnt-=m/i;
m/=i;
}
ans=ans*ksm(i,cnt)%p;
ss[++ss[0]]=i;
}
for(int j=1;j<=ss[0]&&i*ss[j]<=2*n;j++){
prime[ss[j]*i]=1;
if(i%ss[j]==0){
break;
}
}
}
cout<<ans;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号