树状数组：从基础到极致

by hukk

树状数组是一种树形结构的数据结构，可以支持 \(O(\log_2 n)\) 级别的区间操作。

最原始的树状数组仅支持单点修改与区间查询，配合上差分使用可以做到区间修改与单点查询。树状数组在加上各种扩展后可以支持很多其他操作，能够部分赶上并超过线段树的表现，而且其时空复杂度常数显著优于线段树。由于它好写好调，一直以来被许多 OIer 所喜爱。

前置知识

阅读本文，您至少需要了解：
- 常用数学符号如 \(\sum\) 等；
- 前缀和与差分；
- 补码表示法与位运算。
如果您还要阅读本文的进阶部分，您还需要掌握：
- 二维前缀和、差分
- 线段树
- 平衡树
- 可持久化数据结构基础

树状数组基础

概念

引入

考虑以下问题（即洛谷 P3374 【模板】树状数组 1）：

给定长度为 \(n\) 的数列 \(\{a_n\}\) 和 \(m\) 次操作。
操作 1：给定 \(x,k\)，将 \(a_x\) 加上 \(k\)。
操作 2：给定 \(l,r\)，求 \(\sum_{i=l}^r a_i\) 即 \(a_l + a_{l+1} + \cdots + a_{r}\)。

可以发现，无论使用朴素算法或是前缀和都会有一个操作时间复杂度为单次 \(O(n)\)，总复杂度为 \(O(nm)\)。

树状数组可以做到两个操作均为单次 \(O(\log_2 n)\)，接下来介绍它的思想。

数组 d

我们构造一个数组 \(d\)，使它与 \(a\) 有如下对应关系：

\(d\)	\(a\)
\(d_1\)	\(a_1\)
\(d_2\)	\(a_1+a_2\)
\(d_3\)	\(a_3\)
\(d_4\)	\(a_1+a_2+a_3+a_4\)
\(d_5\)	\(a_5\)
\(d_6\)	\(a_5+a_6\)
\(d_7\)	\(a_7\)
\(d_8\)	\(a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8\)
\(d_i\)	\(\sum_{j=i-\operatorname{lowbit}(i)+1}^i a_j\)

把上表画成图就是下面这样的（很经典的图）：

示意图

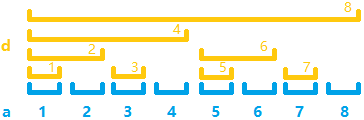
可以发现，在 \(d\) 中：

奇数编号的位置只记录了本身的信息。
2 的整数次幂的位置记录了完整的前缀和。

那其他规律呢？还有表中最后一行的 \(\operatorname{lowbit}\) 是什么意思？

基本操作

lowbit

定义

如果一个正整数 \(x\) 的二进制表示为

\[\begin{matrix} x&=&(1\cdots1\underbrace{00\cdots00})_2\\ &&n\text{个}0 \end{matrix} \]

即末尾有 \(n\) 个 \(0\)，则满足

\[\begin{matrix} \operatorname{lowbit}(x)&=&(1\underbrace{00\cdots00})_2\\ &&n\text{个}0 \end{matrix} \]

也就是说，\(\operatorname{lowbit}(x)\) 就是只保留 \(x\) 在二进制表示下最后一个 \(1\) 及其后的 \(0\)，或者说找到 \(x\) 二进制下最低位的 1 的位置。

举例：

\(5=(101)_2\)，则有 \(\operatorname{lowbit}(5)=(1)_2=1\)。
\(6=(110)_2\)，则有 \(\operatorname{lowbit}(6)=(10)_2=2\)。
\(12=(1100)_2\)，则有 \(\operatorname{lowbit}(12)=(100)_2=4\)。
\(20=(10100)_2\)，则有 \(\operatorname{lowbit}(20)=(100)_2=4\)。

我们再回过头去看图，就能看到：在 \(d\) 中的每个位置都记录了长度为 \(\operatorname{lowbit}(\text{编号})\)、以自身结尾的一段的和。

计算

利用 C++ 中的位运算与补码表示法，可以研究出多种计算 \(\operatorname{lowbit}\) 的方法。以下介绍最常用的一种。

在 C++ 中，有 lowbit(x)=x&-x。

为什么呢？请看下面的表格。

`x`	`-x` 即 `(~x)+1`	`x&-x`
`01...10...00`	`10...10...00` 即 `10...01...11+1`	`10...00`

显然，lowbit(x)=x&-x 是成立的。常定义以下函数：

int lowbit(int x){
    return x&-x;
}

查询与修改

我们已经知道了数组 \(d\) （其实就是树状数组）中记录的信息，怎样才能修改这些信息呢？

为了方便，这里把上面的图搬下来。

示意图

查询

上面讲的树状数组可以 \(O(\log_2 n)\) 查询前缀和，具体是这样的：

先访问将要查询的前缀和的末尾；
向上爬一层，往前走，累加答案；
重复直到已经累加完毕。

例如：查询前 7 项的和。

访问 \(d_7\)；
向上一层，累加 \(d_6\)；
再次向上，累加 \(d_4\)；
查询完毕，结果为 \(d_7+d_6+d_4\)。

像这样，就可以不重不漏地统计每个位置的信息（看看图，\(d_7,d_6,d_4\) 是不是恰好覆盖了 \(a_1,a_2,\cdots a_7\)？）。

如何确定下次加哪个位置呢？很简单：如果你这次累加了 \(d_x\)，那么下一个就是 \(d_{x-\operatorname{lowbit}(x)}\)。也就是循环减 \(\operatorname{lowbit}\)。（不信试试看？）

修改

类似查询，也是一层层往上爬，但是方向变了。

先修改原位置；
向上爬，修改包含原位置信息的后续位置。

例如：修改位置 3，就会改变 \(d_3,d_4,d_8\)。

如何确定下次改哪个位置呢？类似地，如果你这次修改到了 \(d_x\)，那么下一个就是 \(d_{x+\operatorname{lowbit}(x)}\)。也就是循环加 \(\operatorname{lowbit}\)。（同样，自己验证一下？）

至此，你已经学会了树状数组的基本操作了，接下来我们看看它的使用。

使用及代码

建树

在使用之前，一般需要通过原数据构造树状数组，多数人把这个过程称为建树或预处理。

建树有两种方法：

逐个位置修改，复杂度 \(O(n\log_2 n)\)；
利用树状数组的性质，即上面讲的修改的性质递推，复杂度 \(O(n)\)。

详见代码。

//本文中所有代码均设原序列长度为 n，并默认已定义 lowbit()

for(int i=1;i<=n;i++){ //方法 1
    add(i,a[i]); //add 函数，用于修改，参见修改部分代码。
}

for(int i=1;i<=n;i++){ //方法 2
    d[i]+=a[i];
    if(i+lowbit(i)<=n) //注意边界
        d[i+lowbit(i)]+=d[i];
}

查询与修改

前面讲过了，只是要注意边界问题。循环加减 \(\operatorname{lowbit}\) 即可。

代码：

void add(int x,int k){ //在 x 位置上加上 k
    while(x<=n){
        d[x]+=k; //修改
        x+=lowbit(x); //往上爬
    }
}

int query(int x){ //查询前 x 个数的和
    int ans=0;
    while(x>0){
        ans+=d[x]; //累加
        x-=lowbit(x); //往上爬
    }
}

时空复杂度分析

可以看出，树状数组单次操作的时间复杂度与其层数有关。

容易证明，若原序列长度为 \(n\)，则树状数组的层数为 \(\left\lfloor\log_2 n\right\rfloor+1\)，故树状数组单次操作时间复杂度为 \(O(\log_2 n)\)。

同时，树状数组拥有比线段树小得多的时间复杂度常数。（树状数组时间复杂度常数约 \(\dfrac{1}{2}\)，而线段树约为 \(4\)。）

树状数组的空间复杂度为 \(O(n)\)。

应用与变式

区间修改、单点查询

如果使用上述树状数组维护原数组的差分数组，就可以实现区间修改、单点查询。

求逆序对

我们在值域上开树状数组，表示某数是否在序列中出现过(\(0\) 为没出现过，\(1\) 为出现过)。

那么 add 函数就是把数依次加入到序列中，query 函数就是统计序列中值小于等于某数的个数。

我们依次将给定的序列输入，每次输入一个数时，就将当前序列中大于这个数的元素的个数计算出来，并累加到答案，最后的答案就是这个序列的逆序数个数。

若是值域很大，离散化即可。

例题

树状数组进阶

除了最基本的树状数组及其变式，它还有各种高级扩展用法。

二维树状数组

本质上就是用树状数组维护二维前缀和信息，两层循环查询与修改即可。

修改与查询函数变为以下代码：

//设原二维数组有 n 行 m 列

void add(int x,int y,int k){
    for(int i=x;i<=n;i+=lowbit(i))
        for(int j=y;j<=m;j+=lowbit(j))
    	    d[i][j]+=k;
}

int query(int x,int y){
    int ans=0;
    for(int i=x;i>0;i-=lowbit(i))
        for(int j=y;j>0;j-=lowbit(j))
            ans+=d[i][j];
    return ans;
}

树状数组与线段树

区间加法

定义：

\(a\) 为原数组。
\(sum\) 为前缀和数组，记 \(sum[x]=\sum_{i=1}^x a_i\)。
\(delta\) 为差分数组，记 \(\Delta a_x=\sum_{i=1}^x delta[i]\)。

有：

\[\begin{aligned} sum[x]&=\sum_{i=1}^x a_i+\sum_{i=1}^x \left[delta[i]\times(x-i+1)\right]\\ &=\sum_{i=1}^x a_i+x\times\sum_{i=1}^x delta[i]-\sum_{i=1}^x \left[delta[i]\times (i-1)\right] \end{aligned} \]

那么可以把 \(sum\) 拆成三部分维护。具体而言，使用 \(d1\) 维护 \(delta\) 数组的和，\(d2\) 维护 \(delta[i]\times (i-1)\) 的和。详见代码。

void __add(int *arr,int x,int k){
    while(x<=n){
        arr[x]+=k;
        x+=lowbit(x);
    }
}
int __query(int *arr,int x){
    int ans=0;
    while(x>0){
        ans+=arr[x];
        x-=lowbit(x);
    }
    return ans;
}
void add(int l,int r,int x){
    __add(d1,l,x);
    __add(d1,r+1,-x);
    __add(d2,l,x*(l-1));
    __add(d2,r+1,-x*r);
}
int query(int l,int r){
    return (r*__query(d1,r)-(l-1)*__query(d1,l-1))-(__query(d2,r)-__query(d2,l-1));
}

区间最值

普通树状数组的实现要求所维护的数据满足区间加法与区间减法（如区间和），要能由前缀信息得到任意区间信息。

但是区间最值满足区间加法而不满足区间减法，因此需要在原来树状数组上做一些修改。

为了方便对照理解，再次放上这张图：

示意图

以下的代码均以区间最大值为例。

建树

void build(){
     for(int i=1;i<=n;i++){
         int t=lowbit(i);
          d[i]=a[i];
          for(int j=1;j<t;j*=2) //访问该位置能够覆盖的所有位置
              d[i]=max(d[i],d[i-j]);
    }
}

有不理解的，可以对照图片与下面的例子好好体会一下过程。

更新到位置 \(6\)：
更新位置 \(6\)；
访问位置 \(5\)，结束。
更新到位置 \(7\)：
更新位置 \(7\)；
没有需要访问的，结束。
更新到位置 \(8\)：
更新位置 \(8\)；
访问位置 \(8-2^0=7\)；
访问位置 \(8-2^1=6\)；
访问位置 \(8-2^2=4\)；
\(2^3=8\)，不小于 \(8\)，结束。

以上建树过程可以保证正确性与效率兼顾。

修改

换一种建树的方式维护了正确性，修改同样如此。

那么在更新时，我们需要查询更新位置覆盖的所有位置。

void add(int x,int k){
    a[x]=k;
    while(x<=n){
        int t=lowbit(i);
        d[x]=a[x];
        for(int j=1;j<t;j*=2)
            d[i]=max(d[i],d[i-j]);
        x+=lowbit(x);
    }
}

查询

设查询的区间为 \([L,R]\)。

我们从 \(R\) 到 \(L\) 进行判断。\(d_i\) 控制的 \(a\) 数组的元素是 \([i-\operatorname{lowbit}(i)+1,i]\)。设 \(l=i-\operatorname{lowbit}(i)+1,r=i\)。如果 \(L \le l \le R\) 就将 \(d_i\) 加入最值的判断中，接着 \(i\leftarrow (i-\operatorname{lowbit}(i))\)，否则的话就只判 \(a_i\)，然后 \(i\leftarrow(i-1)\)。

代码中的 \(i\) 直接用 \(r\) 来代替，也就是将右端点不断左移。

int query(int l,int r){
    int ans=a[r];
    while(1){
        ans=max(ans,a[r]);
        if(r==l) break;
        r--;
        while(r-l>=lowbit(r))
            ans=max(ans,d[r]),r-=lowbit(r);
        if(r<=l) break;
    }
    return ans;
}

时空复杂度分析

时间复杂度：

建树显然是 \(O(n\log_2 n)\)。
修改和查询均为单次 \(O(\log_2^2 n)\)。

空间复杂度：\(O(n)\)。

例题

P3372 【模板】线段树 1
P1198 【JSOI2008】最大数
P3865 【模板】ST 表（这一道题用树状数组不一定能通过，测试一下正确性就好。）

树状数组与平衡树

可持久化树状数组

参考资料

作者：hukk

本文的全部内容与源代码在 CC BY-SA 4.0 和 SATA 协议之条款下提供，转载请标明原作者。

posted @ 2022-06-04 20:09 hukk 阅读(140) 评论(0) 收藏举报

刷新页面返回顶部

hukk's blog

树状数组：从基础到极致

前置知识

树状数组基础

概念

引入

数组 d

基本操作

lowbit

定义

计算

查询与修改

查询

修改

使用及代码

建树

查询与修改

时空复杂度分析

应用与变式

区间修改、单点查询

求逆序对

例题

树状数组进阶

二维树状数组

树状数组与线段树

区间加法

区间最值

建树

修改

查询

时空复杂度分析

例题

树状数组与平衡树

可持久化树状数组

参考资料

公告