BUAA_OO第一单元总结

第一单元总结

经历了四周的oo课程学习，对本单元进行一个总结。因为第一次次的作业对类的划分提醒的都很明确，所以在总体设计上并没有遇到太大的困难，不过由于自身把握的不到位，所以导致一个类里面的属性和方法都很单一，类之间的交互也极其少，就是更像是写得一个应用了正则表达式的过程式程序，当然也带有一些面向对象的思想。

基于度量来分析自己的程序结构

代码量度量

• 代码量主要集中在paralist.java,poly_item.java两个类中，因为这两个类负责了识别多项式中的项和因子并从中提取指数(exp)和系数(coe)。该过程用到了很多正则匹配的循环，写得冗长了一些。

复杂度分析

方法和类的复杂度分析图片中ev(G)，iv(G)，v(G)，OCavg，WMC含义如下：

• ev(G)即Essentail Complexity，用来表示一个方法的结构化程度，范围在[1,v(G)]之间，值越大则程序的结构越“病态”，其计算过程和图的“缩点”有关。

• iv(G)即Design Complexity，用来表示一个方法和他所调用的其他方法的紧密程度，范围也在[1,v(G)]之间，值越大联系越紧密。

• v(G)即循环复杂度，可以理解为穷尽程序流程每一条路径所需要的试验次数。

• OCavg代表类的方法的平均循环复杂度。

• WMC代表类的总循环复杂度。

类复杂度

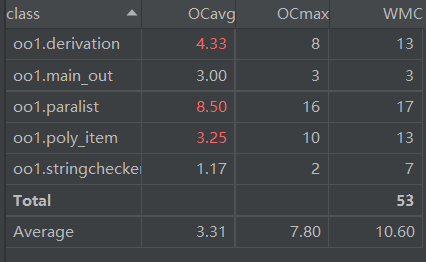
• 平均循环复杂度最高的是paralist.java,因为其负责将“*<因子>”进行识别，提取系数和指数。与之相关的ploy_item.java复杂也出于相近的原因较高，derivation.java是进行求导和化简的类，同时还要生成维护一个HashMap，所以复杂度也较高。

方法复杂度

 

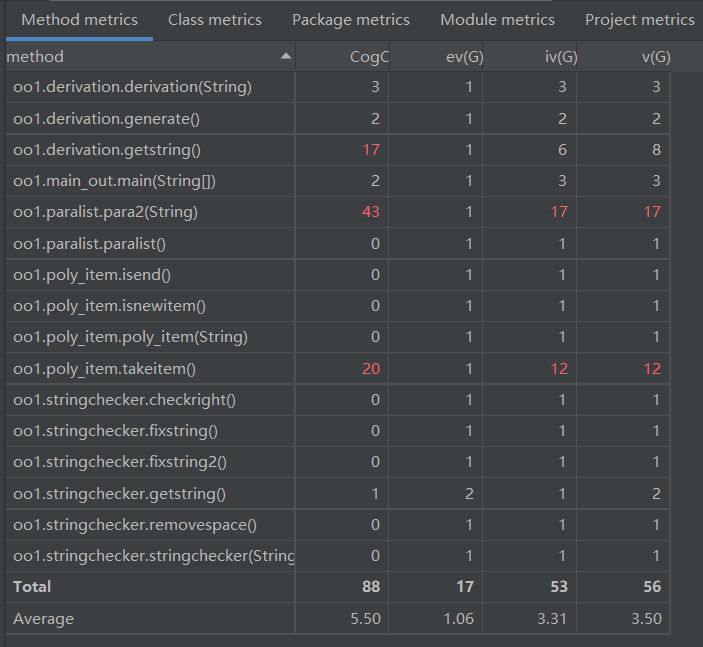
• 度量最高的还是落在了处理项和因子的字符串方法上。同时还注意到这些字符串方法和外边方法联系紧密。在外边的方法中调用了paralist类和poly_item类的public方法，所以造成了依存度高，方法本身复杂度也较高。

类图

 

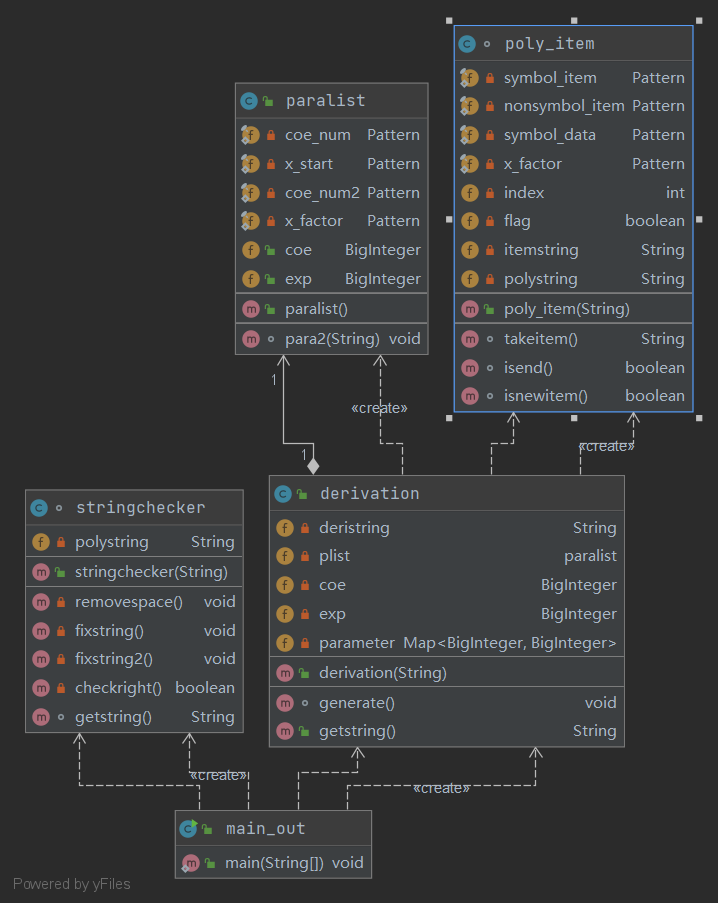
• 第一次作业的设计思路

　　第一次的作业是相对简单的，因为可以将其转化成一般的范式进行过程式处理。函数中出现的因子只有一种类型：即x幂函数类型；出现的项也只有两种：*[+-]k,*x^a;所以我只需要统计这两种形式的函数最终的指数，化简成k*x^a这种形式，输出要是不考虑化简的话甚至可以一步对该表达式求导得出k*a*x^(a-1)这种统一的形式，这样来看第一次作业考虑化简的问题可以说需要做的只有判断正则形式+统计幂函数的次数+合并相同指数的项。

• 程序复杂度

　　在生成derivation.java中的<exp,coe>的HashMap过程中需要不断调用paralist对象，因此会生成大量paralist对象。

分析自己程序的BUG

• 第一次作业并未出现bug，这是因为字符串预处理过饱和，不仅可以全部分析，对于WF的输入也可以分析。因为是可以通过穷举的办法穷尽所有的输入可能。但是这个办法对于只能通过递归下降解决的情况就不适用了，这也是我后面两次作业没完成的主要原因。

分析自己发现别人程序bug所采用的策略

　　在阅读别人代码的过程中，我不仅发现了构造测试集的放法，更重要的是发现了优秀的化简思路。

• 面对采用正则表达式嵌套的代码，可以选择构造复杂度高的样例和特殊格式的样例，以验证其格式判断是否正确，以及递归调用时是否爆栈。因为正则表达式的一些贪心策略不能完全匹配设计初衷，会出现一些意料不到的bug。当然在主体采用递归下降法写格式判断以及因子识别就不易出现这样的错误。
• 对于采用数据结构效率太低的代码，可以构造项与表达式相互嵌套的样例，以验证其遍历效率
• 可以构造多层括号多层嵌套的样例，以攻击其输出效率

感想

　　在本单元作业中，我接触了递归下降分析方法、容器选择的差异以及优化方向，这对我以后的作业和项目开发都有益处。但因为时间较为有限不能很好地完成第二三次作业，这也是第一单元留下的遗憾。