CodeForces 1304F2 Animal Observation (hard version) 题解
一个单调队列的做法。如果你不会的话,可以先去了解一下。
首先,设 \(w_{i,j}\) 表示第\(i\)行第\(j\)个格子的值;设 \(dp_{i,j}\) 表示考虑到第 \(i\) 行,上一行选的左端点是 \(j\)
,且不考虑第 \(i+1\) 行被覆盖的格子时的最大值。
\(dp_{i,j} = max(dp_{i-1,a}+gsum(i,a,a+k-1)+gsum(i,j,j+k-1)-dec)\)
其中, \(gsum(i,l,r)\) 表示第 \(i\) 行里第 \(l\) 至第 \(r\) 个元素的和, \(dec\) 是重叠部分。
直接转移是 \(O(m^2n)\) 的。然而,可以发现,k很小时,很多转移都是无用的。
对于所有的 $a < max(1,j-k+1) $ 和 \(a > min(j+k-1,m-k+1)\) ,都没有重叠部分,所以维护前缀与后缀最大值,把这两部分优化成 \(O(1)\) ,再枚举所有
\(max(1,j-k+1) \leq a \leq min(j+k-1,m-k+1)\)
转移。复杂度 \(O(nmk)\) 可以过 F1 。
F2 怎么搞呢?
先把 $ gsum(i,a,a+k-1)+gsum(i,j,j+k-1)-dec $ 这个东西转化一下。为了方便,把它叫做 \(add\) 。
看这个图。
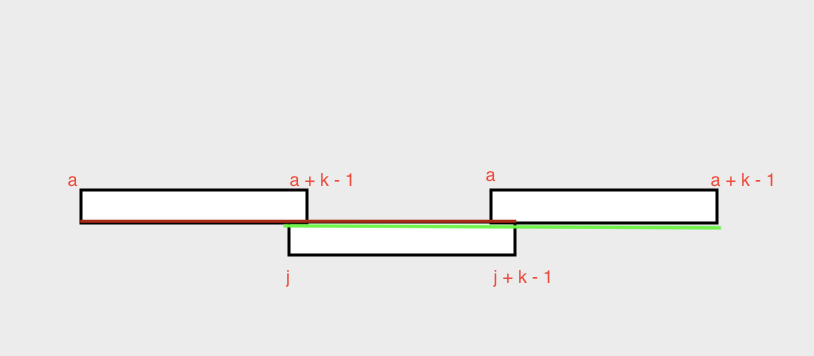
棕色和绿色的线段是增加权值的范围。棕色的\(a \leq k\),绿色的\(a \geq k\)。
这里把它拆成两部分:\(a \leq j\) , 和 \(a \geq j\),先允许它们重叠。
观察一下:
转移时,把第一种和第二种拆开来。
在优化前,先来看看当\(j\)增加\(1\)时,这些值的变化。(下文的\(j\)是原来未增加的)
对于 \(a \leq j\),它的 \(add\) 增加了 \(w_{i,j+k}\),同时可选的状态里, \(a = j - k + 1\) 被移除了,\(a = j + 1\) 被加进来;
对于\(a \geq j\),它的 \(add\) 减少了 \(w_{i,j}\),同时可选的状态里, \(a = j\) 被移除了,\(a = j + k\) 被加进来。
由于所有这些\(add\)都是同时增加,同时减少,相对大小关系不会变。这些在图上画一画可能会帮助理解。
于是可以单调队列优化。开两个队列,对应着两种转移。入队时对于队尾 \(x\) 和进入的元素 \(y\)(\(x\) 和 \(y\) 是下标),比较 \(dp_{i-1,x}+add_x\) 与 \(dp_{i-1,y}+add_y\) 。
时间复杂度 \(O(nm)\) 但是只比log的快了一点点?
代码:
//注意有些实现可能略微不同
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mit map<int,int>::iterator
#define sit set<int>::iterator
#define itrm(g,x) for(mit g=x.begin();g!=x.end();g++)
#define itrs(g,x) for(sit g=x.begin();g!=x.end();g++)
#define ltype int
#define rep(i,j,k) for(ltype(i)=(j);(i)<=(k);(i)++)
#define rap(i,j,k) for(ltype(i)=(j);(i)<(k);(i)++)
#define per(i,j,k) for(ltype(i)=(j);(i)>=(k);(i)--)
#define pii pair<int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
#define fastio ios::sync_with_stdio(false)
const int inf=0x3f3f3f3f,mod=1000000007;
const double pi=3.1415926535897932,eps=1e-6;
int m,n,a[55][20005],pre[20005],suf[20005],dp[55][20005],k,sum[55][20005],val[55][20005];
int gsum(int x,int l,int r){return sum[x][r]-sum[x][l-1];}
int q1[20010],q2[20010],l1,l2,r1,r2;
void push1(int x,int y,int z){
while(dp[z-1][x] + gsum(z,x,y) >dp[z-1][q1[r1]] + gsum(z,q1[r1],y) && r1 >= l1) r1--;
q1[++r1] = x;
}
void pop1(int x){
while(q1[l1] <= x && r1 >= l1) l1++;
}
void push2(int x,int y,int z){
while(dp[z-1][x] + gsum(z,y,x + k - 1) >dp[z-1][q2[r2]] + gsum(z,y,q2[r2] + k - 1) && r2 >= l2) r2--;
q2[++r2] = x;
}
void pop2(int x){
while(q2[l2] <= x && r2 >= l2) l2++;
}//注意这两个pop,是把所有下标小于等于x的弹出
void upd(int x){
rep(i,1,m - k + 1) pre[i]=suf[i]=0;
rep(i,1,m - k + 1) pre[i]=max(pre[i-1],dp[x][i] + val[x+1][i]);
per(i,m - k + 1,1) suf[i]=max(suf[i+1],dp[x][i] + val[x+1][i]);
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
rep(i,1,n) rep(j,1,m) {scanf("%d",&a[i][j]);sum[i][j] = sum[i][j-1] + a[i][j];}
rep(i,1,n) rep(j,1,m - k + 1) val[i][j] = gsum(i, j, j + k - 1);//val[i][j]第i行以第j个元素开始,长度为k的连续段的w值总和
//dp[i][j] 考虑到第i行,且暂时不考虑第(i+1)行的最大值
rep(j,1,m - k + 1) dp[1][j] = val[1][j];
upd(1);
rep(i,2,n){
l1 = l2 = 2;r1 = r2 = 1;//清空
int lst = 0,lst2 = 0;//用来增加状态
rep(j,1,m - k + 1){
int rr = j + k - 1;
int l = max(1,j - k + 1), r = min(m - k + 1,j + k - 1), v=val[i][j];
pop1(l - 1);
pop2(j - 1);//这两个用来弹出已经不能转移的状态,注意我的出队写的有点奇怪
rep(a,lst+1,r) push2(a, j, i);
lst = r;
rep(a,lst2+1,j) push1(a, rr, i);
lst2 = j;// 新状态入队,上面的a覆盖了外面的那个数组
dp[i][j] = max(pre[l - 1],suf[r + 1]) + v;// 第0种,无重叠部分的
int fr1 = q1[l1], fr2 = q2[l2];
dp[i][j] = max(dp[i][j], max(dp[i-1][fr1] + gsum(i,fr1,rr), dp[i-1][fr2] + gsum(i,j,fr2 + k - 1)));//第1种与第2种写在一起了
}
if(i < n) upd(i);//更新前后缀最大值
}
int ans=0;
rep(i,1,m - k + 1) ans=max(ans, dp[n][i]);
printf("%d\n",ans);
return 0;
}
原发表于2月17日。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号