CodeForces 1204E Natasha, Sasha and the Prefix Sums 题解

CF1204E题目链接

好像没人和我做法完全一样？那我就来写一个

首先，声明这个数组是1-indexed的，后面不再赘述。

设某种最大前缀和等于 \(x\) ，共有 \(num_x\) 个。所有的总和，可以用 \(\sum x \times num_x\) 算。但是直接用dp之类的计算每个 \(num_x\) 有些困难，换种思路。

枚举一个序列中，前缀的最大值 \(val\) 和第一次达到最大值的位置 \(p\) （这里设为第一次，是为了方便计数，设成最后一次也可以）。尝试计算所有这样的序列的数目。这样肯定不会重复计数。

容易发现，对于所有的\(1 \leq i<p\)，都有 \(pre_i<pre_p\) （这段连上 \(p\) 本身，称为“前面”）；对于所有的 \(p < i \leq n+m\) ，都有 \(pre_i \leq pre_p\) （这段称为“后面”）。

同时，由\(p\)和\(val\)可以反推出前面和后面的 \(1\) 和 \(-1\) 的数量，前面 \(1\) 的数量为 \((p+val)/2\) ，就设为 \(num1\) 吧（当然 \(num1\) 不是整数的情况要判掉）。剩下的可填位置数小于剩下 \(1\) 的数量的情况，也要判掉，不然可能会有负数下标。

总合法序列数量，就是前面的填法数 \(front\) 和后面的填法数量 \(back\) 的乘积。

\(back\) 可能好算一些，就是“共有多少个序列长度为 \((n+m-p)\) ，有 \((m-num1)\) 个 \(1\) ，且每个前缀都不大于 \(0\) ”， \(n^2\) 的dp就可以算。

至于 \(front\) ，把前面的条件变形一下。

\(pre_i<pre_p\) 移项得 \(pre_p-pre_i>0\) ，这个"\(pre_p-pre_i\)"是什么呢？

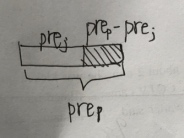
也就是说，它是以\(p\)为结尾的一个后缀。这个后缀必须小于\(0\)。注意到可以翻转，后缀可以看成与前缀等价，用另一个dp就能算出来。

具体地说一下我的dp， \(f_{i,j}\) 表示长度为 \(i\) 、有 \(j\) 个 \(1\) 的序列中，所有前缀和都不小于 \(0\) 的序列的数量。把这样的序列中所有数取相反数，也就是把 \(j\) 变成 \(i-j\) ，就变成了所有前缀和都不大于 \(0\) 的数量了。类似地， \(g_{i,j}\) 表示所有非空前缀的前缀和都小于 \(0\) 的序列的数量。

具体转移不难，看代码吧。

\(k\) 就等于 \(n+m\) 。

原来的程序（少一个判断）可能会越界，在本机上测都有问题，但在CF上没测出来，直接AC了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mit map<int,int>::iterator
#define sit set<int>::iterator
#define itrm(g,x) for(mit g=x.begin();g!=x.end();g++)
#define itrs(g,x) for(sit g=x.begin();g!=x.end();g++)
#define ltype int
#define rep(i,j,k) for(ltype(i)=(j);(i)<=(k);(i)++)
#define rap(i,j,k) for(ltype(i)=(j);(i)<(k);(i)++)
#define per(i,j,k) for(ltype(i)=(j);(i)>=(k);(i)--)
#define pii pair<int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
#define fastio ios::sync_with_stdio(false)
const int inf=0x3f3f3f3f,mod=998244853;
const double pi=3.1415926535897932,eps=1e-6;
int n,m,f[4005][4005],g[4005][2005],ans,k;
#define check(i) if(i>=mod) i-=mod;
int main()
{
   scanf("%d%d",&n,&m);
   k=n+m;
   f[0][0]=1;
   rep(i,1,k) rep(j,0,min(i,k)) //这里必须是min(i,n+m)，后面调用f时第二维会到n以上
   if(2*j>=i){
       if(j>0) f[i][j]=f[i-1][j-1];
       f[i][j]+=f[i-1][j];
       check(f[i][j]);
   }
   g[0][0]=1;
   rep(i,1,k) rep(j,0,min(i,n)) if(2*j>i){
       if(j>0) g[i][j]=g[i-1][j-1];
       g[i][j]+=g[i-1][j];
       check(g[i][j]);
   }
   rep(p,1,k) rep(val,1,min(p,n)){
       if((p+val)&1) continue;
       int num1=(p+val)/2;
       if(num1>n||k-p<n-num1) continue;//这里就是之前错的原因了，k-p<n-num1的话，肯定不会合法。        
       ans+=(ll)g[p][num1]*f[k-p][k-p-(n-num1)]%mod*val%mod;
       check(ans);
   }
   printf("%d\n",ans);
   return 0;
}

原发表于2月4日。