离散数学左孝凌版本-----第三章集合论一

集合论

集合与关系

集合的概念

略

集合表示法

略

集合相等定义

基本概念

子集

空集

全集

幂集

集合的运算

序偶

笛卡尔积

总结

关系及其表示

总结

关系性质

特殊关系的性质：

空关系： 反自反性，对称性，反对称性，传递性
全域关系：自反性，对称性，传递性
恒等关系：自反性，对称性，传递性

复合关系和逆关系

行x*列y=结果第x行第y个，y先移动

经典相互包含证明（上

逆关系:
R是X到Y的二元关系，把R中每一序偶的元素次序颠倒，得到的关系称为R的逆关系，记作R^c:

闭包运算

通过适当补充序偶使某关系扩充成具有特定特征的新关系

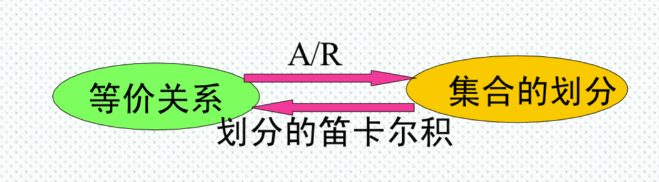
划分与覆盖

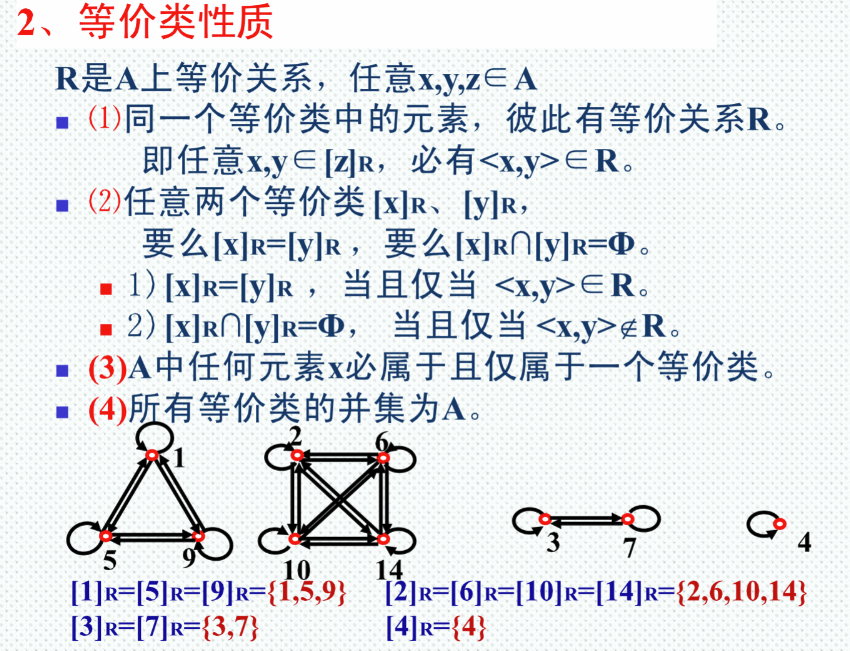
等价关系与等价类

若集合A上的关系R，满足自反性，对称性，传递性，则称R为A上的等价关系。

等价类：
商集：

R是A上等价关系，由R的所有等价类构成的集合，称为A关于R的商集。记作A/R。
即

等价关系与划分

相容关系