01.先导

凸优化是优化问题的一种。优化等价于数学规划。

优化：从一个可行解的集合中，寻找最优的元素。

1. 数学优化

优化问题可以写为如下的形式：

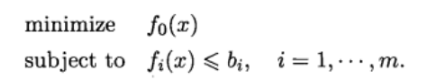
式中的\(x=[x_1,x_2,...,x_n]^T\) 称为优化变量。\(f_0\) 为目标函数，\(f_i\) 是目标函数的约束函数，\(f_i(x)\leqslant b_i\) 是一个不等式约束。优化问题就是找出最优的\(x\)，一般记为\(x^*\)。即对于任意满足约束\(f_1(z)\le b_1,...,f_m(z)\le b_m\) 的向量\(z\) ,都有\(f_0(z)\ge f_0(x^*)\) 。\(f_1(z)\le b_1,...,f_m(z)\le b_m\) 就是可行解(feasible set)。

最优解通常不会只有一个，会是一个最优解集。