01-数组

1. 理论基础

数组是存放在连续内存空间上的相同类型数据的集合。
为了指代数组中的特定位置或元素，可以指定数组的名称和特定元素在数组中的位置编号。数组名称遵循与其他变量名相同的约定。

数组的简单示例：

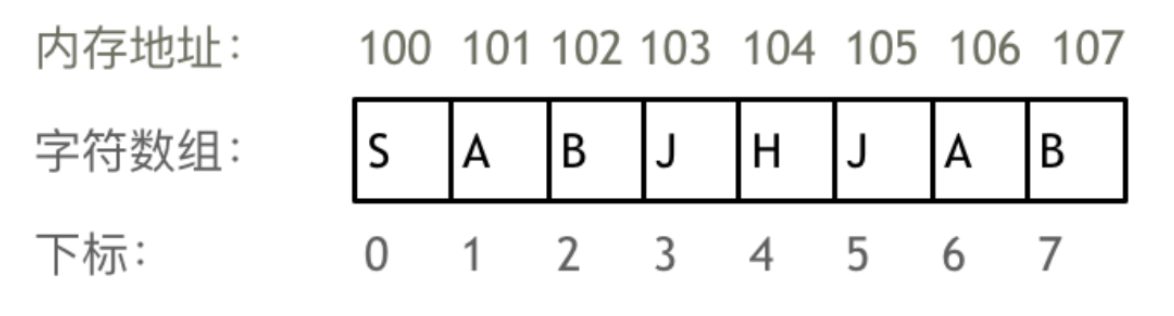
数组内存空间的地址是连续的
正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

在C++中需要注意vector和array的区别，vector是容器，底层实现是array。

数组的元素是不能删除的，只能覆盖。

C++中二维数组的地址是连续的。

在数组中访问元素非常高效，我们可以在 𝑂(1) 时间内随机访问数组中的任意一个元素。

1.1 数组的优点与局限性

数组存储在连续的内存空间内，且元素类型相同。这种做法包含丰富的先验信息，系统可以利用这些信息来优化数据结构的操作效率。
‧ 空间效率高：数组为数据分配了连续的内存块，无须额外的结构开销。
‧ 支持随机访问：数组允许在 𝑂(1) 时间内访问任何元素。
‧ 缓存局部性：当访问数组元素时，计算机不仅会加载它，还会缓存其周围的其他数据，从而借助高速缓存来提升后续操作的执行速度。
连续空间存储是一把双刃剑，其存在以下局限性。
‧ 插入与删除效率低：当数组中元素较多时，插入与删除操作需要移动大量的元素。
‧ 长度不可变：数组在初始化后长度就固定了，扩容数组需要将所有数据复制到新数组，开销很大。
‧ 空间浪费：如果数组分配的大小超过实际所需，那么多余的空间就被浪费了。

2. 二分查找

二分查找即为：

给定⼀个 n 个元素有序的（升序）整型数组 nums 和⼀个目标值 target ，写⼀个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

写二分法，区间的定义⼀般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

2.1 闭区间写法

定义 target 是在⼀个在左闭右闭的区间里，也就是[left, right]

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]⼀定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

class Solution{
public:
    int search(vector<int>& nums,int target){
        int left=0;
        int right=nums.size()-1;
        while(left<=right){
            int middle=left+((right-left)/2);
            if(nums[middle]>target){
                right=middle-1;
            }
            else if(nums[middle]<target){
                left=middle+1;
            }
            else{
                return middle;
            }
        }
        return -1;
    }
    
};

2.2 开区间写法

如果说定义 target 是在⼀个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。
有如下两点：

while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下⼀个查询区间不会去比较nums[middle]

class Solution{
public:
    int search(vector<int>& nums,int target){
        int left=0;
        int right=nums.size();
        while(left<right){
            int middle=left+((right-left)>>1);
            if(nums[middle]>target){
                right=middle;
            }
            else if(nums[middle]<target){
                left=middle+1;
            }
            else{
                return middle;
            }
        }
        return -1;
    }
};

在C++中，

>>1  等价于 /2
<<1  等价于 *2

2.3 例题(leetcode)

leetcode(34)

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

提示：

算两次正常的二分查找即可，只需要找等于target的值。

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int left=0;
        int right=nums.size()-1;
        int first=-1;
        int last=-1;
        while(left<=right){
            int middle=left+((right-left)/2);

            if(nums[middle]==target){
                first=middle;
                right=middle-1;
            }
            else if(nums[middle]>target){
                right=middle-1;
            }
            else{
                left=middle+1;
            }
        }

        left=0;
        right=nums.size()-1;
        while(left<=right){
            int middle=left+((right-left)/2);
            if(nums[middle]==target){
                last=middle;
                left=middle+1;
            }
            else if(nums[middle]>target){
                right=middle-1;
            }
            else{
                left=middle+1;
            }
        }

        return vector<int>{first,last};

    }
};

leetcode(35)

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

提示：

考虑这个插入的位置 pos，它成立的条件为：

nums[pos−1]<target≤nums[pos]
其中 nums 代表排序数组。由于如果存在这个目标值，我们返回的索引也是 pos，因此我们可以将两个条件合并得出最后的目标：「在一个有序数组中找第一个大于等于 target 的下标」。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size()-1;

        while(left <= right){
            int middle = left+((right-left)/2);
            if(nums[middle]<target){
                left = middle+1;
            }
            else{
                right=middle-1;
            }
        }
        return left;
    }
};

leetcode(69)

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

提示：

使用二分查找的方法计算整数的平方根。x 平方根的整数部分 ans 是满足\(k^2 \le x\)的最大 k 值，因此我们可以对 k 进行二分查找。

class Solution {
public:
    int mySqrt(int x) {
        int left=0;
        int right=x;
        int ans=-1;
        while(left<=right){
            int middle=left+((right-left)/2);
            if((long long)midddle*middle<=x){
                ans=middle;
                left=middle+1;
            }else{
                right=middle-1;
            }
        }
        return ans;
    }
};

leetcode(367)

给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如 sqrt 。

考虑使用二分查找来优化方法二中的搜索过程。因为 num 是正整数，所以若正整数 x 满足 x×x=num，则 x 一定满足 1≤x≤num。于是我们可以将 1 和 num 作为二分查找搜索区间的初始边界。

细节

因为我们在移动左侧边界 left 和右侧边界 right 时，新的搜索区间都不会包含被检查的下标 mid，所以搜索区间的边界始终是我们没有检查过的。因此，当left=right 时，我们仍需要检查 mid=(left+right)/2。

class Solution {
public:
    bool isPerfectSquare(int num) {
        int left = 0, right = num;
        while (left <= right) {
            int mid = (right - left) / 2 + left;
            long square = (long) mid * mid;
            if (square < num) {
                left = mid + 1;
            } else if (square > num) {
                right = mid - 1;
            } else {
                return true;
            }
        }
        return false;
    }
};

3. 移除元素

4.有序数组的平方

posted @ 2024-08-30 10:31 yyyyyllll 阅读(40) 评论(0) 收藏举报

刷新页面返回顶部

yyyylllll

01-数组

1. 理论基础

1.1 数组的优点与局限性

2. 二分查找

2.1 闭区间写法

2.2 开区间写法

2.3 例题(leetcode)

leetcode(34)

leetcode(35)

leetcode(69)

leetcode(367)

3. 移除元素

4.有序数组的平方

公告