数据挖掘与分析课程笔记

数据挖掘与分析课程笔记

• 参考教材：Data Mining and Analysis : MOHAMMED J.ZAKI, WAGNER MEIRA JR.

Chapter 1 ：准备

1.1 数据矩阵

Def.1. 数据矩阵是指一个 \((n\times d)\) 的矩阵

\[\mathbf{D}=\left(\begin{array}{c|cccc} & X_{1} & X_{2} & \cdots & X_{d} \\ \hline \mathbf{x}_{1} & x_{11} & x_{12} & \cdots & x_{1 d} \\ \mathbf{x}_{2} & x_{21} & x_{22} & \cdots & x_{2 d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathbf{x}_{n} & x_{n 1} & x_{n 2} & \cdots & x_{n d} \end{array}\right) \]

行：实体，列：属性

Ex. 鸢尾花数据矩阵

\[\left(\begin{array}{c|ccccc} & 萼片长 & 萼片宽 & 花瓣长 & 花瓣宽 & 类别 \\ & X_{1} & X_{2} & X_{3} & X_{4} & X_{5} \\ \hline \mathbf{x}_{1} & 5.9 & 3.0 & 4.2 & 1.5 & 云芝 \\ \end{array}\right) \]

1.2 属性

Def.2.

• 数值属性 是指取实数值（或整数值）的属性。
• 若数值属性的取值范围是有限集或无限可数集，则称之为离散数值属性。若只有两种取值，则称为二元属性。
• 若数值属性的取值范围不是离散的则称为连续数值属性。

Def.3. 类别属性 是指取值为符号的属性。

1.3 代数与几何的角度

假设 \(\mathbf{D}\) 中所有属性均为数值的，即

\[\mathbf{x}_{i}=\left(x_{i 1}, x_{i 2}, \ldots, x_{i d}\right)^{T} \in \mathbb{R}^{d},i=1,\cdots,n \]

或

\[\mathbf{x}_{j}=\left(x_{1 j}, x_{2j}, \ldots, x_{n j}\right)^{T} \in \mathbb{R}^{n},j=1,\cdots,d \]

☆ 默认向量为列向量。

1.3.1 距离与角度

设 \(\mathbf{a}, \mathbf{b} \in \mathbb{R}^{d}\) ，

• 点乘：\(\mathbf{a}^{T}\mathbf{b}=\sum\limits_{i=1}^{d} a_ib_i\)
• 长度（欧氏范数）：\(\left | \mathbf{a} \right | =\sqrt{\mathbf{a}^{T}\mathbf{a} } =\sqrt{\sum\limits_{i=1}^{d} a_i^2}\)，单位化：\(\frac{\mathbf{a}}{|\mathbf{a}|}\)
• 距离：\(\delta(\mathbf{a},\mathbf{b})=||\mathbf{a}-\mathbf{b}||=\sqrt{\sum\limits_{i=1}^{d}(a_i-b_i)^2}\)
• 角度：\(cos \theta =(\frac{\mathbf{a}}{|\mathbf{a}|})^{T}(\frac{\mathbf{b}}{|\mathbf{b}|})\)，即单位化后作点乘
• 正交：\(\mathbf{a}\) 与 \(\mathbf{b}\) 正交，若 \(\mathbf{a}^{T}\mathbf{b}=0\)

1.3.2 算术平均与总方差

Def.3.

• 算术平均：\(mean(\mathbf{D})=\hat{\boldsymbol{\mu}}=\frac{1}{n} \sum\limits_{i=1}^n\mathbf{x}_i,\in \mathbb{R}^{d}\)

• 总方差：\(var(\mathbf{D})=\frac{1}{n} \sum\limits_{i=1}^{n} \delta\left(\mathbf{x}_{i}, \hat{\boldsymbol{\mu}}\right)^{2}\)

  自行验证：\(var(\mathbf{D})=\frac{1}{n} \sum\limits_{i=1}^{n}||\mathbf{x}_{i}- \hat{\boldsymbol{\mu}}||^2=\frac{1}{n} \sum\limits_{i=1}^{n}||\mathbf{x}_{i}||^2-||\hat{\boldsymbol{\mu}}||^2\)

• 中心数据矩阵：\(center(\mathbf{D})=\begin{pmatrix} \mathbf{x}_{1}^T - \hat{\boldsymbol{\mu}}^T\\ \vdots \\ \mathbf{x}_{n}^T - \hat{\boldsymbol{\mu}}^T \end{pmatrix}\)

  显然 \(center(\mathbf{D})\) 的算术平均为 \(\mathbf{0}\in \mathbb{R}^{d}\)

1.3.3 正交投影

Def.4. \(\mathbf{a}, \mathbf{b} \in \mathbb{R}^{d}\)，向量 \(\mathbf{b}\) 沿向量 \(\mathbf{a}\) 方向的正交分解是指，将 \(\mathbf{b}\) 写成：\(\mathbf{b}= \mathbf{p}+ \mathbf{r}\)。其中，\(\mathbf{p}\) 是指 \(\mathbf{b}\) 在 \(\mathbf{a}\) 方向上的正交投影，\(\mathbf{r}\) 是指 \(\mathbf{a}\) 与 \(\mathbf{b}\) 之间的垂直距离。

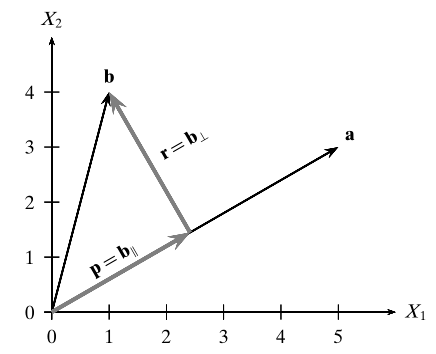
\(\mathbf{a}\ne\mathbf{0},\mathbf{b}\ne\mathbf{0}\)

设 \(\mathbf{p}=c\cdot\mathbf{a},(c \ne 0,c \in \mathbb{R})\) 则 \(\mathbf{r}=\mathbf{b}-\mathbf{p}=\mathbf{b}-c\mathbf{a}\)

\(0 = \mathbf{p}^T\mathbf{r} = (c\cdot\mathbf{a})^T(\mathbf{b}-c\mathbf{a})=c\cdot(\mathbf{a}^T\mathbf{b}-c\cdot\mathbf{a}^T\mathbf{a})\)

\(c= \frac{\mathbf{a}^T\mathbf{b}}{\mathbf{a}^T\mathbf{a}}, \mathbf{p}=\frac{\mathbf{a}^T\mathbf{b}}{\mathbf{a}^T\mathbf{a}}\cdot\mathbf{a}\)

1.3.4 线性相关性与维数

皆与线性代数相同，自读。

1.4 概率观点

每一个数值属性 \(X\) 被视为一个随机变量，即 \(X:\mathcal{O}\rightarrow \mathbb{R}\)，

其中，\(\mathcal{O}\) 表示 \(X\) 的定义域，即所有实验可能输出的集合，即样本空间。\(\mathbb{R}\) ：\(X\) 的值域，全体实数。

☆ 注：

• 随机变量是一个函数。
• 若 \(\mathcal{O}\) 本身是数值的（即 \(\mathcal{O}\subseteq \mathbb{R}\)，那么 \(X\) 是恒等函数，即 \(X(v)=v\)
• 若 \(X\) 的函数取值范围为有限集或无限可数集，则称之为离散随机变量，反之，为连续随机变量

Def.5. 若 \(X\) 是离散的，那么 \(X\) 的概率质量函数（probability mass function, PMF）为：

\[\forall x \in \mathbb{R},f(x)=P(X=x) \]

注：\(f(x)\ge0,\sum\limits_xf(x)=1\)；\(f(x)=0\)，如果 \(x\notin\) (\(x\) 的值域)。

Def.6. 若 \(X\) 是连续的，那么 \(X\) 的概率密度函数（probability density function, PDF）为：

\[P(X\in [a,b])=\int_{a}^{b} f(x)dx \]

注：\(f(x)\ge0,\int_{-\infty}^{+\infty}f(x)=1\)

Def.7. 对任意随机变量 \(X\) ，定义累积分布函数（cumulative distributution function, CDF）

\[F:\mathbb{R}\to[0,1],\forall x\in \mathbb{R},F(x)=P(X\le x) \]

若 \(X\) 是离散的，\(F(x)=\sum\limits_{u\le x}f(u)\)

若 \(X\) 是连续的，\(F(x)=\int_{-\infty}^xf(u)du\)

1.4.1 二元随机变量

\(\mathbf{X}=\left ( \begin{matrix} X_1 \\ X_2 \end{matrix} \right ), \mathbf{X}:\mathcal{O}\to\mathbb{R}^2\) 此处 \(X_1\)，\(X_2\) 分别是两个随机变量。

上课时略去了很多概念，补上。

Def.8. 若 \(X_1\) 和 \(X_2\) 都是离散，那么 \(\mathbf{X}\) 的联合概率质量函数被定义为：

\[f(\mathbf{x})=f(x_1,x_2)=P(X_1=x_1,X_2=x_2)=P(\mathbf{X}=\mathbf{x}) \]

注：\(f(x)\ge0,\sum\limits_{x_1}\sum\limits_{x_2}f(x_1,x_2)=1\)

Def.9. 若 \(X_1\) 和 \(X_2\) 都是连续，那么 \(\mathbf{X}\) 的联合概率密度函数被定义为：

\[P(\mathbf{X} \in W)=\iint\limits_{\mathbf{x} \in W} f(\mathbf{x}) d \mathbf{x}=\iint\limits_{\left(x_{1}, x_{2}\right)^T_{\in} W} f\left(x_{1}, x_{2}\right) d x_{1} d x_{2} \]

其中，\(W \subset \mathbb{R}^2\)，\(f(\mathbf{x})\ge0,\iint\limits_{\mathbf{x}\in\mathbb{R}^2}f(\mathbf{x})d\mathbf{x}=1\)

Def.10. \(\mathbf{X}\) 的联合累积分布函数 \(F\)

\[F(x_1,x_2)=P(X_1\le x_1 \text{ and } X_2\le x_2)=P(\mathbf{X}\le\mathbf{x}) \]

Def.11. \(X_1\) 和 \(X_2\) 是独立的，如果 \(\forall W_1\subset \mathbb{R}\) 及 \(\forall W_2\subset \mathbb{R}\)

\[P(X_1\in W_1 \text{ and } X_2\in W_2)=P(X_1\in W_1)\cdot(X_2\in W_2) \]

Prop. 如果 \(X_1\) 和 \(X_2\) 是独立的，那么

\[F(x_1,x_2)=F_1(x_1)\cdot F_2(x_2)\\ f(x_1,x_2)=f_1(x_1)\cdot f_2(x_2) \]

其中 \(F_i\) 是 \(X_i\) 的累积分布函数，\(f_i\) 是 \(x_i\) 的 PMF 或 PDF。

1.4.2 多元随机变量

平行推广1.4.1节中的各定义即可。

1.4.3 随机样本与统计量

Def.12. 给定随机变量 \(X\) ，来源于 \(X\) 的长度为 \(n\) 的随机样本是指 \(n\) 个独立的且同分布（均与 \(X\) 具有同样的 PMF 或 PDF）的随机变量 \(S_1,S_2,\cdots,S_n\)。

Def.13. 统计量 \(\hat{\theta}\) 被定义为关于随机样本的函数 \(\hat{\theta}:(S_1,S_2,\cdots,S_n)\to \mathbb{R}\)

注： \(\hat{\theta}\) 本身也是随机变量

Chapter 2：数值属性

关注代数、几何与统计观点。

2.1 一元分析

仅关注一项属性，\(\mathbf{D}=\left(\begin{array}{c} X \\ \hline x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right),x_i\in\mathbb{R}\)

统计： \(X\) 可视为（高维）随机变量，\(x_i\) 均是恒等随机变量，\(x_1,\cdots,x_n\) 也看作源于 \(X\) 的长度为 \(n\) 的随机样本。

Def.1. 经验积累分布函数

Def.2. 反积累分布函数

Def.3. 随机变量 \(X\) 的经验概率质量函数是指

\[\hat{f}(x)=\frac{1}{n} \sum_{i=1}^{n} I\left(x_{i} = x\right),\forall x_i \in \mathbb{R}\\ I\left(x_{i} = x\right)=\left\{\begin{matrix} 1,x_i=x\\ 0,x_i\ne x \end{matrix}\right. \]

2.1.1 集中趋势量数

Def.4. 离散随机变量 \(X\) 的期望是指：\(\mu:=E(X) = \sum\limits_{x} xf(x)\)，\(f(x)\) 是 \(X\) 的PMF

连续随机变量 \(X\) 的期望是指：\(\mu:=E(X) = \int\limits_{-\infin}^{+\infin} xf(x)dx\)，\(f(x)\) 是 \(X\) 的PDF

注：\(E(aX+bY)=aE(X)+bE(Y)\)

Def.5. \(X\) 的样本平均值是指 \(\hat{\mu}=\frac{1}{n} \sum\limits_{i=1}^{n}x_i\)，注 \(\hat{\mu}\) 是 \(\mu\) 的估计量

Def.6. 一个估计量（统计量）\(\hat{\theta}\) 被称作统计量 \(\theta\) 的无偏估计，如果 \(E(\hat{\theta})=\theta\)

自证：样本平均值 \(\hat{\mu}\) 是期望 \(\mu\) 的无偏估计量，\(E(x_i)=\mu \text{ for all } x_i\)

Def.7. 一个估计量是稳健的，如果它不会被样本中的极值影响。（样本平均值并不是稳健的。）

Def.8. 随机变量 \(X\) 的中位数

Def.9. 随机变量 \(X\) 的样本中位数

Def.10. 随机变量 \(X\) 的众数， 随机变量 \(X\) 的样本众数

2.2.2 离差量数

Def.11. 随机变量 \(X\) 的极差与样本极差

Def.12. 随机变量 \(X\) 的四分位距，样本的四分位距

Def.13. 随机变量 \(X\) 的方差是

\[\sigma^{2}=\operatorname{var}(X)=E\left[(X-\mu)^{2}\right]=\left\{\begin{array}{ll} \sum_{x}(x-\mu)^{2} f(x) & \text { if } X \text { is discrete } \\ \\ \int_{-\infty}^{\infty}(x-\mu)^{2} f(x) d x & \text { if } X \text { is continuous } \end{array}\right. \]

标准差 \(\sigma\) 是指 \(\sigma^2\) 的正的平方根。

注：方差是关于期望的第二阶动差，\(r\) 阶动差是指 \(E[(x-\mu)^r]\)。

性质：

1. \(\sigma^2=E(X^2)-\mu^2=E(X^2)-[E(X)]^2\)
2. \(var(X_1+X_2)=var(X_1)+var(X_2)\)，\(X_1,X_2\) 独立

Def.14. 样本方差是 \(\hat{\sigma}^{2}=\frac{1}{n} \sum\limits_{i=1}^{n}\left(x_{i}-\hat{\mu}\right)^{2}\)，底下非 \(n-1\)

样本方差的几何意义：考虑中心化数据矩阵

\[C:=\left(\begin{array}{c} x_{1}-\hat{\mu} \\ x_{2}-\hat{\mu} \\ \vdots \\ x_{n}-\hat{\mu} \end{array}\right)\\ n\cdot \hat{\sigma}^2=\sum\limits_{i=1}^{n}\left(x_{i}-\hat{\mu}\right)^{2}=||C||^2 \]

问题：\(X\) 的样本平均数的期望与方差？

\[E(\hat{\mu})=E(\frac{1}{n} \sum\limits_{i=1}^{n}x_i)=\frac{1}{n} \sum\limits_{i=1}^{n} E(x_i)=\frac{1}{n}\sum\limits_{i=1}^{n}\mu=\mu\\ \]

方差有两种方法：第一种直接展开，第二种：运用 \(x_1,\cdots,x_n\) 独立同分布：

\[var(\sum\limits_{i=1}^{n}x_i))=\sum\limits_{i=1}^{n}var(x_i)=n\cdot \sigma^2\Longrightarrow var(\hat{\mu})=\frac{\sigma^2}{n} \]

注：样本方差是有偏估计，因为：\(E(\sigma^2)=(\frac{n-1}{n})\sigma^2\xrightarrow{n\to +\infin}\sigma^2\)

2.2 二元分析

略

2.3 多元分析

\[\mathbf{D}=\left(\begin{array}{c|cccc} & X_{1} & X_{2} & \cdots & X_{d} \\ \hline \mathbf{x}_{1} & x_{11} & x_{12} & \cdots & x_{1 d} \\ \mathbf{x}_{2} & x_{21} & x_{22} & \cdots & x_{2 d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathbf{x}_{n} & x_{n 1} & x_{n 2} & \cdots & x_{n d} \end{array}\right) \]

可视为：\(\mathbf{X}=(X_1,\cdots,X_d)^T\)

Def.15. 对于随机变量向量 \(\mathbf{X}\)，其期望向量为：\(E[\mathbf{X}]=\left(\begin{array}{c} E\left[X_{1}\right] \\ E\left[X_{2}\right] \\ \vdots \\ E\left[X_{d}\right] \end{array}\right)\)

样本平均值为：\(\hat{\boldsymbol{\mu}}=\frac{1}{n} \sum\limits_{i=1}^{n} \mathbf{x}_{i},(=mean(\mathbf{D})) \in \mathbb{R}^{d}\)

Def.16. 对于 \(X_1,X_2\)，定义协方差 \(\sigma_{12}=E[(X_1-E(X_1))(X_2-E(X_2)]=E(X_1X_2)-E(X_1)E(X_2)\)

Remark:

1. \(\sigma_{12}=\sigma_{21}\)
2. 若两者独立，则 \(\sigma_{12}=0\)

Def.17. 对于随机变量向量 \(\mathbf{X}=(X_1,\cdots,X_d)^T\)，定义协方差矩阵：

\[\boldsymbol{\Sigma}=E\left[(\mathbf{X}-\boldsymbol{\mu})(\mathbf{X}-\boldsymbol{\mu})^{T}\right]=\left(\begin{array}{cccc} \sigma_{1}^{2} & \sigma_{12} & \cdots & \sigma_{1 d} \\ \sigma_{21} & \sigma_{2}^{2} & \cdots & \sigma_{2 d} \\ \cdots & \cdots & \cdots & \cdots \\ \sigma_{d 1} & \sigma_{d 2} & \cdots & \sigma_{d}^{2} \end{array}\right)_{d\times d} \]

其为对称矩阵，定义 \(\mathbf{X}\) 的广义方差为 \(det(\boldsymbol{\Sigma})\)

注：

1. \(\boldsymbol{\Sigma}\) 是实对称矩阵且半正定，即所有特征值非负，\(\lambda_1\ge \lambda_2 \cdots \ge\lambda_d \ge 0\)
2. \(var(\mathbf{D})=tr(\Sigma)=\sigma_1^2+\cdots+\sigma_d^2\)

Def.18. 对于 \(\mathbf{X}=(X_1,\cdots,X_d)^T\)，定义样本协方差矩阵

\[\hat{\boldsymbol{\Sigma}}=\frac{1}{n}\left(\mathbf{Z}^{T} \mathbf{Z}\right)=\frac{1}{n}\left(\begin{array}{cccc} Z_{1}^{T} Z_{1} & Z_{1}^{T} Z_{2} & \cdots & Z_{1}^{T} Z_{d} \\ Z_{2}^{T} Z_{1} & Z_{2}^{T} Z_{2} & \cdots & Z_{2}^{T} Z_{d} \\ \vdots & \vdots & \ddots & \vdots \\ Z_{d}^{T} Z_{1} & Z_{d}^{T} Z_{2} & \cdots & Z_{d}^{T} Z_{d} \end{array}\right)_{d\times d} \]

其中

\[\mathbf{Z}=\mathbf{D}-\mathbf{1} \cdot \hat{\boldsymbol{\mu}}^{T}=\left(\begin{array}{c} \mathbf{x}_{1}^{T}-\hat{\boldsymbol{\mu}}^{T} \\ \mathbf{x}_{2}^{T}-\hat{\boldsymbol{\mu}}^{T} \\ \vdots \\ \mathbf{x}_{n}^{T}-\hat{\boldsymbol{\mu}}^{T} \end{array}\right)=\left(\begin{array}{ccc} -& \mathbf{z}_{1}^{T} & - \\ -& \mathbf{z}_{2}^{T} & - \\ & \vdots \\ -& \mathbf{z}_{n}^{T} & - \end{array}\right)=\left(\begin{array}{cccc} \mid & \mid & & \mid \\ Z_{1} & Z_{2} & \cdots & Z_{d} \\ \mid & \mid & & \mid \end{array}\right)\]

样本总方差是 \(tr(\hat{\boldsymbol{\Sigma}})\)，广义样本方差是 \(det(\hat{\boldsymbol{\Sigma}})\ge0\)

\(\hat{\boldsymbol{\Sigma}}=\frac{1}{n}\sum\limits_{i=1}^n\mathbf{z}_{i}\mathbf{z}_{i}^T\)

Chapter 5 Kernel Method：核方法

Example 5.1 略，\(\phi(核映射):\Sigma^*(输入空间)\to \mathbb{R}^4(特征空间)\)

Def.1. 假设核映射 \(\phi:\mathcal{I}\to \mathcal{F}\)，\(\phi\) 的核函数是指 \(K:\mathcal{I}\times\mathcal{I}\to \mathbb{R}\) 使得 \(\forall (\mathbf{x}_i,\mathbf{x}_j)\in \mathcal{I}\times\mathcal{I},K(\mathbf{x}_i,\mathbf{x}_j)=\phi^T(\mathbf{x}_i)\phi(\mathbf{x}_j)\)

Example 5.2 设 \(\phi:\mathbb{R}^2\to \mathbb{R}^3\) 使得 \(\forall \mathbf{a}=(a_1，a_2),\phi(\mathbf{a})=(a_1^2,a_2^2,\sqrt2a_1a_2)^T\)

注意到 \(K(\mathbf{a},\mathbf{b})=\phi(\mathbf{a})^T\phi(\mathbf{b})=a_1^2b_1^2+a_2^2b_2^2+2a_1^2a_2^2b_1^2b_2^2\)，\(K:\mathbb{R}^2\times\mathbb{R}^2\to \mathbb{R}\)

Remark：

1. 分析复杂数据
2. 分析非线性特征（知乎搜核函数有什么作用）

Goal：在未知 \(\phi\) 的情况下，通过分析 \(K\) 来分析特征空间 \(\mathcal{F}\) 结果。

5.1 核矩阵

设 \(\mathbf{D}=\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{n}\right\} \subset \mathcal{I}\)，其核矩阵定义为：\(\mathbf{K}=[K(\mathbf{x}_{i},\mathbf{x}_{j})]_{n\times n}\)

Prop. 核矩阵 \(\mathbf{K}\) 是对称的且半正定的

Proof. \(K(\mathbf{x}_{i},\mathbf{x}_{j})=\phi^T(\mathbf{x}_i)\phi(\mathbf{x}_j)=\phi^T(\mathbf{x}_j)\phi(\mathbf{x}_i)=K(\mathbf{x}_{j},\mathbf{x}_{i})\)，故对称。

对于 \(\forall \mathbf{a}^{T}\in \mathbb{R}^n\)，

\[\begin{aligned} \mathbf{a}^{T} \mathbf{K a} &=\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \\ &=\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) \\ &=\left(\sum_{i=1}^{n} a_{i} \phi\left(\mathbf{x}_{i}\right)\right)^{T}\left(\sum_{j=1}^{n} a_{j} \phi\left(\mathbf{x}_{j}\right)\right) \\ &=\left\|\sum_{i=1}^{n} a_{i} \phi\left(\mathbf{x}_{i}\right)\right\|^2 \geq 0 \end{aligned} \]

5.1.1 核映射的重构

”经验核映射“

已知 \(\mathbf{D}=\left\{\mathbf{x}_{i}\right\}_{i=1}^{n} \subset \mathcal{I}\) 与核矩阵 \(\mathbf{K}\)

目标：寻找 \(\phi:\mathcal{I} \to \mathcal{F} \subset \mathbb{R}^n\)

首先尝试：\(\forall \mathbf{x} \in \mathcal{I},\phi(\mathbf{x})=\left(K\left(\mathbf{x}_{1}, \mathbf{x}\right), K\left(\mathbf{x}_{2}, \mathbf{x}\right), \ldots, K\left(\mathbf{x}_{n}, \mathbf{x}\right)\right)^{T} \in \mathbb{R}^{n}\)

检查：\(\phi^T(\mathbf{x}_i)\phi(\mathbf{x}_j)?=K(\mathbf{x}_{i},\mathbf{x}_{j})\)

左边 \(=\phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right)=\sum\limits_{k=1}^{n} K\left(\mathbf{x}_{k}, \mathbf{x}_{i}\right) K\left(\mathbf{x}_{k}, \mathbf{x}_{j}\right)=\mathbf{K}_{i}^{T} \mathbf{K}_{j}\)，\(\mathbf{K}_{i}\) 代表第 \(i\) 行或列要求太高。

考虑改进：寻找矩阵 \(\mathbf{A}\) 使得，\(\mathbf{K}_{i}^{T} \mathbf{A} \mathbf{K}_{j}=\mathbf{K}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)\)，即 \(\mathbf{K}^{T} \mathbf{A} \mathbf{K}=\mathbf{K}\)

故只需取 \(\mathbf{A}=\mathbf{K}^{-1}\) 即可（ \(\mathbf{K}\) 可逆）

若 \(\mathbf{K}\) 正定，\(\mathbf{K}^{-1}\) 也正定，即存在一个实矩阵 \(\mathbf{B}\) 满足 \(\mathbf{K}^{-1}=\mathbf{B}^{T}\mathbf{B}\)

故经验核函数可定义为：

\[\phi(\mathbf{x})=\mathbf{B}\cdot\left(K\left(\mathbf{x}_{1}, \mathbf{x}\right), K\left(\mathbf{x}_{2}, \mathbf{x}\right), \ldots, K\left(\mathbf{x}_{n}, \mathbf{x}\right)\right)^{T} \]

检查：\(\phi^T(\mathbf{x}_i)\phi(\mathbf{x}_j)=(\mathbf{B}\mathbf{K}_i)^T(\mathbf{B}\mathbf{K}_j)=\mathbf{K}_i^T\mathbf{K}^{-1}\mathbf{K}_j=(\mathbf{K}^T\mathbf{K}^{-1}\mathbf{K})_{i,j}=K(\mathbf{x}_{i},\mathbf{x}_{j})\)

5.1.2 特定数据的海塞核映射

对于对称半正定矩阵 \(\mathbf{K}_{n\times n}\)，存在分解

\[\mathbf{K}=\mathbf{U}\left(\begin{array}{cccc} \lambda_{1} & 0 & \cdots & 0 \\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{array}\right)\mathbf{U}^{T}=\mathbf{U}\boldsymbol{\Lambda}\mathbf{U}^{T} \]

\(\lambda_{i}\) 为特征值，\(\mathbf{U}=\left(\begin{array}{cccc} \mid & \mid & & \mid \\ \mathbf{u}_{1} & \mathbf{u}_{2} & \cdots & \mathbf{u}_{n} \\ \mid & \mid & & \mid \end{array}\right)\) 为单位正交矩阵，\(\mathbf{u}_{i}=\left(u_{i 1}, u_{i 2}, \ldots, u_{i n}\right)^{T} \in \mathbb{R}^{n}\) 为特征向量，即

\[\mathbf{K}=\lambda_{1} \mathbf{u}_{1} \mathbf{u}_{1}^{T}+\lambda_{2} \mathbf{u}_{2} \mathbf{u}_{2}^{T}+\cdots+\lambda_{n} \mathbf{u}_{n} \mathbf{u}_{n}^{T}\\ \begin{aligned} \mathbf{K}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) &=\lambda_{1} u_{1 i} u_{1 j}+\lambda_{2} u_{2 i} u_{2 j} \cdots+\lambda_{n} u_{n i} u_{n j} \\ &=\sum_{k=1}^{n} \lambda_{k} u_{k i} u_{k j} \end{aligned} \]

定义海塞映射：

\[\forall \mathbf{x}_i \in \mathbf {D}, \phi\left(\mathbf{x}_{i}\right)=\left(\sqrt{\lambda_{1}} u_{1 i}, \sqrt{\lambda_{2}} u_{2 i}, \ldots, \sqrt{\lambda_{n}} u_{n i}\right)^{T} \]

检查：

\[\begin{aligned} \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) &=\left(\sqrt{\lambda_{1}} u_{1 i}, \ldots, \sqrt{\lambda_{n}} u_{n i}\right)\left(\sqrt{\lambda_{1}} u_{1 j}, \ldots, \sqrt{\lambda_{n}} u_{n j}\right)^{T} \\ &=\lambda_{1} u_{1 i} u_{1 j}+\cdots+\lambda_{n} u_{n i} u_{n j}=K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \end{aligned} \]

注意：海塞映射中仅对 \(\mathbf{D}\) 中的数 \(\mathbf{x}_i\) 有定义。

5.2 向量核函数

\(\mathbb{R}^d \times \mathbb{R}^d \to \mathbb{R}\)

典型向量核函数：多项式核

\(\forall \mathbf{x},\mathbf{y} \in \mathbb {R}^d, K_{q}(\mathbf{x}, \mathbf{y})=\phi(\mathbf{x})^{T} \phi(\mathbf{y})=\left(\mathbf{x}^{T} \mathbf{y} + c \right)^{q}\)，其中 \(c\ge 0\)

若 \(c=0\)，齐次，否则为非齐次。

问题：构造核映射 \(\phi:\mathbb{R}^d \to \mathcal{F}\)，使得 \(K_{q}(\mathbf{x}, \mathbf{y})=\phi(\mathbf{x})^{T} \phi(\mathbf{y})\)

注：\(q=1,c=0, \phi (\mathbf{x})=\mathbf{x}\)

示例：\(q=2,d=2\)

高斯核自读

5.3 特征空间中基本核运算

\(\phi:\mathcal{I} \to \mathcal{F}, K:\mathcal{I} \times \mathcal{I}\to \mathbb{R}\)

• 向量长度：\(\|\phi(\mathbf{x})\|^{2}=\phi(\mathbf{x})^{T} \phi(\mathbf{x})=K(\mathbf{x}, \mathbf{x})\)

• 距离：

  \[\begin{aligned} \left\|\phi\left(\mathbf{x}_{i}\right)-\phi\left(\mathbf{x}_{j}\right)\right\|^{2} &=\left\|\phi\left(\mathbf{x}_{i}\right)\right\|^{2}+\left\|\phi\left(\mathbf{x}_{j}\right)\right\|^{2}-2 \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) \\ &=K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)+K\left(\mathbf{x}_{j}, \mathbf{x}_{j}\right)-2 K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \end{aligned} \]

\(2 K\left(\mathbf{x}, \mathbf{y}\right)=\left\|\phi\left(\mathbf{x}\right)\right\|^{2}+\left\|\phi\left(\mathbf{y}\right)\right\|^{2}-\left\|\phi\left(\mathbf{x}\right)-\phi\left(\mathbf{y}\right)\right\|^{2}\)

代表 \(\phi\left(\mathbf{x}\right)\) 与 \(\phi\left(\mathbf{y}\right)\) 的相似度

• 平均值：\(\boldsymbol{\mu}_{\phi}=\frac{1}{n} \sum\limits_{i=1}^{n} \phi\left(\mathbf{x}_{i}\right)\)

  \[\begin{aligned} \left\|\boldsymbol{\mu}_{\phi}\right\|^{2} &=\boldsymbol{\mu}_{\phi}^{T} \boldsymbol{\mu}_{\phi} \\ &=\left(\frac{1}{n} \sum\limits_{i=1}^{n} \phi\left(\mathbf{x}_{i}\right)\right)^{T}\left(\frac{1}{n} \sum\limits_{j=1}^{n} \phi\left(\mathbf{x}_{j}\right)\right) \\ &=\frac{1}{n^{2}} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) \\ &=\frac{1}{n^{2}} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \end{aligned} \]

• 总方差：\(\sigma_{\phi}^{2}=\frac{1}{n} \sum\limits_{i=1}^{n}\left\|\phi\left(\mathbf{x}_{i}\right)-\boldsymbol{\mu}_{\phi}\right\|^{2}\)，\(\forall \mathbf{x}_{i}\)

  \[\begin{aligned} \left\|\phi\left(\mathbf{x}_{i}\right)-\boldsymbol{\mu}_{\phi}\right\|^{2} &=\left\|\phi\left(\mathbf{x}_{i}\right)\right\|^{2}-2 \phi\left(\mathbf{x}_{i}\right)^{T} \boldsymbol{\mu}_{\phi}+\left\|\boldsymbol{\mu}_{\phi}\right\|^{2} \\ &=K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)-\frac{2}{n} \sum_{j=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)+\frac{1}{n^{2}} \sum_{s=1}^{n} \sum_{t=1}^{n} K\left(\mathbf{x}_{s}, \mathbf{x}_{t}\right) \end{aligned} \]
  \[\begin{aligned} \sigma_{\phi}^{2} &=\frac{1}{n} \sum\limits_{i=1}^{n}\left\|\phi\left(\mathbf{x}_{i}\right)-\boldsymbol{\mu}_{\phi}\right\|^{2}\\ &=\frac{1}{n} \sum\limits_{i=1}^{n}\left(K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)-\frac{2}{n} \sum\limits_{j=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)+\frac{1}{n^{2}} \sum\limits_{s=1}^{n} \sum\limits_{t=1}^{n} K\left(\mathbf{x}_{s}, \mathbf{x}_{t}\right)\right)\\ &=\frac{1}{n} \sum\limits_{i=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)-\frac{2}{n^{2}} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)+\frac{1}{n^{2}} \sum\limits_{s=1}^{n} \sum\limits_{t=1}^{n} K\left(\mathbf{x}_{s}, \mathbf{x}_{t}\right)\\ &=\frac{1}{n} \sum\limits_{i=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)-\frac{1}{n^{2}} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) \end{aligned} \]

  \(\frac{1}{n} \sum\limits_{i=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)\) 是 \(\mathbf{K}\) 对角线平均值，\(\frac{1}{n^{2}} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)\) 是 \(\mathbf{K}\) 所有元的平均值。

• 中心化核矩阵：令 \(\hat{\phi}\left(\mathbf{x}_{i}\right)=\phi\left(\mathbf{x}_{i}\right)-\boldsymbol{\mu}_{\phi}\)

  中心核函数 \(\hat{K}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) =\hat{\phi}\left(\mathbf{x}_{i}\right)^{T} \hat{\phi}\left(\mathbf{x}_{j}\right)\)

  \[\begin{aligned} \hat{K}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) &=\left(\phi\left(\mathbf{x}_{i}\right)-\boldsymbol{\mu}_{\phi}\right)^{T}\left(\phi\left(\mathbf{x}_{j}\right)-\boldsymbol{\mu}_{\phi}\right) \\ &=\phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right)-\phi\left(\mathbf{x}_{i}\right)^{T} \boldsymbol{\mu}_{\phi}-\phi\left(\mathbf{x}_{j}\right)^{T} \boldsymbol{\mu}_{\phi}+\boldsymbol{\mu}_{\phi}^{T} \boldsymbol{\mu}_{\phi}\\ &=K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)-\frac{1}{n} \sum_{k=1}^{n} \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{k}\right)-\frac{1}{n} \sum_{k=1}^{n} \phi\left(\mathbf{x}_{j}\right)^{T} \phi\left(\mathbf{x}_{k}\right)+\left\|\boldsymbol{\mu}_{\phi}\right\|^{2} \\ &=K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)-\frac{1}{n} \sum_{k=1}^{n} K\left(\mathbf{x}_{i}, \mathbf{x}_{k}\right)-\frac{1}{n} \sum_{k=1}^{n} K\left(\mathbf{x}_{j}, \mathbf{x}_{k}\right)+\frac{1}{n^{2}} \sum_{s=1}^{n} \sum_{t=1}^{n} K\left(\mathbf{x}_{s}, \mathbf{x}_{t}\right) \end{aligned} \]

  故

  \[\begin{aligned} \hat{\mathbf{K}} &=\mathbf{K}-\frac{1}{n} \mathbf{1}_{n \times n} \mathbf{K}-\frac{1}{n} \mathbf{K} \mathbf{1}_{n \times n}+\frac{1}{n^{2}} \mathbf{1}_{n \times n} \mathbf{K} \mathbf{1}_{n \times n} \\ &=\left(\mathbf{I}-\frac{1}{n} \mathbf{1}_{n \times n}\right) \mathbf{K}\left(\mathbf{I}-\frac{1}{n} \mathbf{1}_{n \times n}\right) \end{aligned} \]

  注意：\(\mathbf{1}_{n \times n}\) 为全1矩阵，左乘之后每个元素为之前所在列的列和，右乘之和每个元素为之前所在行的行和，左右都乘之后每个元素即为原来所以元素之后。

• 归一化核矩阵

  \(\mathbf{K}_{n}\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\frac{\phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right)}{\left\|\phi\left(\mathbf{x}_{i}\right)\right\| \cdot\left\|\phi\left(\mathbf{x}_{j}\right)\right\|}=\frac{K\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)}{\sqrt{K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right) \cdot K\left(\mathbf{x}_{j}, \mathbf{x}_{j}\right)}}\)

  令 \(\mathbf{W}=\operatorname{diag}(\mathbf{K})=\left(\begin{array}{cccc} K\left(\mathbf{x}_{1}, \mathbf{x}_{1}\right) & 0 & \cdots & 0 \\ 0 & K\left(\mathbf{x}_{2}, \mathbf{x}_{2}\right) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & K\left(\mathbf{x}_{n}, \mathbf{x}_{n}\right) \end{array}\right)\)，则 \(\mathbf{W}^{-1 / 2}\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)=\frac{1}{\sqrt{K\left(\mathbf{x}_{i}, \mathbf{x}_{i}\right)}}\)，

  \(\mathbf{K}_{n}=\mathbf{W}^{-1 / 2} \cdot \mathbf{K} \cdot \mathbf{W}^{-1 / 2}\)

  矩阵左乘右乘对角阵的性质。

5.4 复杂对象的核

5.4.1 字串的谱核

考虑字符集 \(\Sigma\) （有限），定义 \(l\)-谱特征映射：

\[\phi_l: \Sigma^{*} \rightarrow \mathbb{R}^{|\Sigma|^l},\forall \mathbf{x} \in \Sigma^{*},\phi_l(\mathbf{x})=\left ( \cdots,\#(\alpha),\cdots \right )^T \]

其中 \(\#(\alpha)\) 代表长度为 \(l\) 的子字串在 \(\mathbf{x}\) 中出现的次数。

\(l\)-谱核函数：\(\mathbf{K}_l:\Sigma^{*} \times \Sigma^{*} \to \mathbb{R}\)，\(\mathbf{K}_l (\mathbf{x},\mathbf{y})=\phi_l(\mathbf{x})^{T} \phi_l(\mathbf{y})\)

谱核函数：计算 \(l=0\) 到 \(l=\infty\)

5.4.2 图顶点的扩散核

• 图：图 \(G=(V,E)\) 是指一个集合对，其中 \(V=\{v_1,\cdots,v_n\}\) 为顶点集，\(E=\{(v_i,v_j)\}\) 为边集。现只考虑无向简单（没有自己到自己的边）图。

• 邻接矩阵：图的邻接矩阵 \(A(G):=[A_{ij}]_{n\times n}\)，其中 \(A_{ij}=\left\{\begin{matrix} 1, (v_i,v_j)\in E\\ 0, (v_i,v_j) \notin E \end{matrix}\right.\)

• 度矩阵：\(\Delta (G):=diag(d_1,\cdots,d_n)\)，其中 \(d_i\) 代表顶点 \(v_i\) 的度，即与 \(v_i\) 相连的边的数目。

• 拉普拉斯矩阵：\(L(G):=A(G)-\Delta(G)\)

  负拉普拉斯矩阵：\(L(G):=-L(G)\)

  它们是实对称

常用图的对称相似性矩阵 \(\mathbf{S}\) 是指 \(A(G)\)，\(L(G)\) 或 \(-L(G)\)。

问题：如何定义图顶点的核函数？（ \(\mathbf{S}\) 并不一定是半正定）

- 幂核函数

以 \(\mathbf{S}^t\) 作为核矩阵， \(\mathbf{S}\) 是对称的，\(t\) 为正整数

考虑 \(\mathbf{S}^2\)：\(\mathbf{S}^2(x_i,x_j)=\sum\limits_{k=1}^{n}S_{ik}S_{kj}\)

此公式说明 \(\mathbf{S}^2\) ( \(\mathbf{S}^l\)) 的几何意义：顶点间长度为 \(2\) \((l)\) 的路径，描述顶点的相似性。

考虑 \(\mathbf{S}^l\) 的特征值：设 \(\mathbf{S}\) 的特征值为 \(\lambda_1,\cdots,\lambda_n \in \mathbb{R}\)，则

\[\mathbf{S}=\mathbf{U}\left(\begin{array}{cccc} \lambda_{1} & 0 & \cdots & 0 \\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \end{array}\right)\mathbf{U}^{T}=\sum_{i=1}^{n} \lambda_{i}\mathbf{u}_{i} \mathbf{u}_{i}^{T} \]

其中 \(\mathbf{U}\) 是以相应特征向量为列的正交矩阵，\(\mathbf{U}=\left(\begin{array}{cccc} \mid & \mid & & \mid \\ \mathbf{u}_{1} & \mathbf{u}_{2} & \cdots & \mathbf{u}_{n} \\ \mid & \mid & & \mid \end{array}\right)\)

\[\mathbf{S}^l=\mathbf{U}\left(\begin{array}{cccc} \lambda_{1}^l & 0 & \cdots & 0 \\ 0 & \lambda_{2}^l & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_{n}^l \end{array}\right)\mathbf{U}^{T} \]

\(\lambda_1^l,\cdots,\lambda_n^l\) 是 \(\mathbf{S}^l\) 的特征值。

故若 \(l\) 是偶数，\(\mathbf{S}^l\) 半正定。

- 指数扩散核函数

以 \(\mathbf{K}:=e^{\beta \mathbf{S}}\) 为核矩阵，其中 \(\beta >0\) 为阻尼系数。（泰勒展开：\(e^{\beta x}=\sum\limits_{l=0}^{\infin}\frac{1}{l!}\beta^{l}x^l\)）

\[\begin{aligned} e^{\beta \mathbf{S}} &=\sum_{l=0}^{\infty} \frac{1}{l !} \beta^{\prime} \mathbf{S}^{l} \\ &=\mathbf{I}+\beta \mathbf{S}+\frac{1}{2 !} \beta^{2} \mathbf{S}^{2}+\frac{1}{3 !} \beta^{3} \mathbf{S}^{3}+\cdots\\ &=\left(\sum_{i=1}^{n} \mathbf{u}_{i} \mathbf{u}_{i}^{T}\right)+\left(\sum_{i=1}^{n} \mathbf{u}_{i} \beta \lambda_{i} \mathbf{u}_{i}^{T}\right)+\left(\sum_{i=1}^{n} \mathbf{u}_{i} \frac{1}{2 !} \beta^{2} \lambda_{i}^{2} \mathbf{u}_{i}^{T}\right)+\cdots \\ &=\sum_{i=1}^{n} \mathbf{u}_{i}\left(1+\beta \lambda_{i}+\frac{1}{2 !} \beta^{2} \lambda_{i}^{2}+\cdots\right) \mathbf{u}_{i}^{T} \\ &=\sum_{i=1}^{n} \mathbf{u}_{i} e ^{\beta \lambda_{i}} \mathbf{u}_{i}^{T} \\ &=\mathbf{U}\left(\begin{array}{cccc} e ^{\beta \lambda_{1}} & 0 & \cdots & 0 \\ 0 & e ^{\beta \lambda_{2}} & \cdots & 0 \\ \vdots & \vdots & \ddots & 0 \\ 0 & 0 & \cdots & e ^{\beta \lambda_{n}} \end{array}\right) \mathbf{U}^{T} \end{aligned} \]

故 \(\mathbf{K}\) 的特征值 \(e ^{\beta \lambda_{1}},\cdots,e ^{\beta \lambda_{n}}\) 完全非负， \(\mathbf{K}\) 为半正定。

- 纽因曼扩散核函数

以 \(\mathbf{K}=\sum\limits_{l=0}^{\infty} \beta^l \mathbf{S}^l\) 为核矩阵，注意到

\[\begin{aligned} \mathbf{K} &=\mathbf{I}+\beta \mathbf{S}+\beta^{2} \mathbf{S}^{2}+\beta^{3} \mathbf{S}^{3}+\cdots \\ &=\mathbf{I}+\beta \mathbf{S}\left(\mathbf{I}+\beta \mathbf{S}+\beta^{2} \mathbf{S}^{2}+\cdots\right) \\ &=\mathbf{I}+\beta \mathbf{S} \mathbf{K} \end{aligned} \]

故

\[\begin{aligned} \mathbf{K}-\beta \mathbf{S} \mathbf{K} &=\mathbf{I} \\ (\mathbf{I}-\beta \mathbf{S}) \mathbf{K} &=\mathbf{I} \\ \mathbf{K} &=(\mathbf{I}-\beta \mathbf{S})^{-1} \end{aligned} \]

在 \(\mathbf{I}-\beta \mathbf{S}\) 可逆的前提下

\[\begin{aligned} \mathbf{K} &=\left(\mathbf{U} \mathbf{U}^{T}-\mathbf{U}(\beta \mathbf{\Lambda}) \mathbf{U}^{T}\right)^{-1} \\ &=\left(\mathbf{U}(\mathbf{I}-\beta \mathbf{\Lambda}) \mathbf{U}^{T}\right)^{-1} \\ &=\mathbf{U}(\mathbf{I}-\beta \mathbf{\Lambda})^{-1} \mathbf{U}^{T}\\ &=\mathbf{U}\left(\begin{array}{cccc} \frac{1}{1-\beta\lambda_1} & 0 & \cdots & 0 \\ 0 & \frac{1}{1-\beta\lambda_2} & \cdots & 0 \\ \vdots & \vdots & \ddots & 0 \\ 0 & 0 & \cdots & \frac{1}{1-\beta\lambda_n} \end{array}\right) \mathbf{U}^{T} \end{aligned} \]

要想其半正定，故有：

\[\begin{aligned} \left(1-\beta \lambda_{i}\right)^{-1} & \geq 0 \\ 1-\beta \lambda_{i} & \geq 0 \\ \beta \lambda_{i} & \leq 1 \end{aligned} \]

Chapter 7：降维

PCA：主元分析

7.1 背景

\[\mathbf{D}=\left(\begin{array}{c|cccc} & X_{1} & X_{2} & \cdots & X_{d} \\ \hline \mathbf{x}_{1} & x_{11} & x_{12} & \cdots & x_{1 d} \\ \mathbf{x}_{2} & x_{21} & x_{22} & \cdots & x_{2 d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathbf{x}_{n} & x_{n 1} & x_{n 2} & \cdots & x_{n d} \end{array}\right) \]

对象：\(\mathbf{x}_{1}^T,\cdots,\mathbf{x}_n^T \in \mathbb{R}^d\)，\(\forall \mathbf{x} \in \mathbb{R}^d,\) 设 \(\mathbf{x}=(x_1,\cdots,x_d)^T= \sum\limits_{i=1}^{d}x_i \mathbf{e}_i\)

其中，\(\mathbf{e}_i=(0,\cdots,1,\cdots,0)^T\in\mathbb{R}^d\)，i-坐标

设另有单位正交基 \(\{\mathbf{u}\}_{i=1}^n\)，\(\mathbf{x}=\sum\limits_{i=1}^{d}a_i \mathbf{u}_i,a_i \in \mathbb{R}\)，\(\mathbf{u}_i^T \mathbf{u}_j =\left\{\begin{matrix} 1,i=j\\ 0,i\ne j \end{matrix}\right.\)

\(\forall r:1\le r\le d, \mathbf{x}=\underbrace{a_1 \mathbf{u}_1+\cdots+a_r \mathbf{u}_r}_{\text{投影}}+ \underbrace{a_{r+1} \mathbf{u}_{r+1}+\cdots+a_d \mathbf{u}_d}_{\text{误差}}\)

前 \(r\) 项是投影，后面是投影误差。

目标：对于给定 \(D\)，寻找最优 \(\{\mathbf{u}\}_{i=1}^n\)，使得 \(D\) 在其前 \(r\) 维子空间的投影是对 \(D\) 的“最佳近似”，即投影之后“误差最小”。

7.2 主元分析：

7.2.1 最佳直线近似

（一阶主元分析）（r=1）

目标：寻找 \(\mathbf{u}_1\)，不妨记为 \(\mathbf{u}=(u_1,\cdots,u_d)^T\)。

假设：\(||\mathbf{u}||=\mathbf{u}^T\mathbf{u}=1\)，\(\hat{\boldsymbol{\mu}}=\frac{1}{n} \sum\limits_{i=1}^n\mathbf{x}_i=\mathbf{0},\in \mathbb{R}^{d}\)

\(\forall \mathbf{x}_i(i=1,\cdots,n)\)，\(\mathbf{x}_i\) 沿 \(\mathbf{u}\) 方向投影是：

\[\mathbf{x}_{i}^{\prime}=\left(\frac{\mathbf{u}^{T} \mathbf{x}_{i}}{\mathbf{u}^{T} \mathbf{u}}\right) \mathbf{u}=\left(\mathbf{u}^{T} \mathbf{x}_{i}\right) \mathbf{u}=a_{i} \mathbf{u},a_{i}=\mathbf{u}^{T} \mathbf{x}_{i} \]

\(\hat{\boldsymbol{\mu}}=\mathbf{0}\Rightarrow\) \(\hat{\boldsymbol{\mu}}\) 在 \(\mathbf{u}\) 上投影是0；\(\mathbf{x}_{1}^{\prime},\cdots,\mathbf{x}_{n}^{\prime}\) 的平均值为0 。

\(Proj(mean(D))=mean{Proj(D)}\)

考察 \(\mathbf{x}_{1}^{\prime},\cdots,\mathbf{x}_{n}^{\prime}\) 沿 \(\mathbf{u}\) 方向的样本方差：

\[\begin{aligned} \sigma_{\mathbf{u}}^{2} &=\frac{1}{n} \sum_{i=1}^{n}\left(a_{i}-\mu_{\mathbf{u}}\right)^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\mathbf{u}^{T} \mathbf{x}_{i}\right)^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n} \mathbf{u}^{T}\left(\mathbf{x}_{i} \mathbf{x}_{i}^{T}\right) \mathbf{u} \\ &=\mathbf{u}^{T}\left(\frac{1}{n} \sum_{i=1}^{n} \mathbf{x}_{i} \mathbf{x}_{i}^{T}\right) \mathbf{u} \\ &=\mathbf{u}^{T} \mathbf{\Sigma} \mathbf{u} \end{aligned} \]

\(\mathbf{\Sigma}\) 是样本协方差矩阵。

目标：

\[\begin{array}{ll} \max\limits_{\mathbf{u}} & \mathbf{u}^{T} \mathbf{\Sigma} \mathbf{u} \\ \text{s.t} & \mathbf{u}^T\mathbf{u}-1=0 \end{array} \]

应用 Lagrangian 乘数法：

\[\max \limits_{\mathbf{u}} J(\mathbf{u})=\mathbf{u}^{T} \Sigma \mathbf{u}-\lambda\left(\mathbf{u}^{T} \mathbf{u}-1\right) \]

求偏导：

\[\begin{aligned} \frac{\partial}{\partial \mathbf{u}} J(\mathbf{u}) &=\mathbf{0} \\ \frac{\partial}{\partial \mathbf{u}}\left(\mathbf{u}^{T} \mathbf{\Sigma} \mathbf{u}-\lambda\left(\mathbf{u}^{T} \mathbf{u}-1\right)\right) &=\mathbf{0} \\ 2 \mathbf{\Sigma} \mathbf{u}-2 \lambda \mathbf{u} &=\mathbf{0} \\ \mathbf{\Sigma} \mathbf{u} &=\lambda \mathbf{u} \end{aligned} \]

注意到：\(\mathbf{u}^{T} \mathbf{\Sigma} \mathbf{u}=\mathbf{u}^{T} \lambda \mathbf{u}=\lambda\)

故优化问题的解 \(\lambda\) 选取 \(\mathbf{\Sigma}\) 最大特征值， \(\mathbf{u}\) 选与 \(\lambda\) 相应的单位特征向量。

问题：上述问题使得 \(\sigma_{\mathbf{u}}^{2}\) 最大的 \(\mathbf{u}\) 能否使投影误差最小？

定义平均平方误差（Minimum Squared Error，MSE）：

\[\begin{aligned} M S E(\mathbf{u}) &=\frac{1}{n} \sum_{i=1}^{n}\left\|\mathbf{x}_{i}-\mathbf{x}_{i}^{\prime}\right\|^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\mathbf{x}_{i}-\mathbf{x}_{i}^{\prime}\right)^{T}\left(\mathbf{x}_{i}-\mathbf{x}_{i}^{\prime}\right) \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\left\|\mathbf{x}_{i}\right\|^{2}-2 \mathbf{x}_{i}^{T} \mathbf{x}_{i}^{\prime}+\left(\mathbf{x}_{i}^{\prime}\right)^{T} \mathbf{x}_{i}^{\prime}\right)\\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\left\|\mathbf{x}_{i}\right\|^{2}-2 \mathbf{x}_{i}^{T} (\mathbf{u}^{T} \mathbf{x}_{i})\mathbf{u}+\left[(\mathbf{u}^{T} \mathbf{x}_{i})\mathbf{u}\right]^{T} \left[ (\mathbf{u}^{T} \mathbf{x}_{i})\mathbf{u}\right] \right)\\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\left\|\mathbf{x}_{i}\right\|^{2}-2 (\mathbf{u}^{T} \mathbf{x}_{i})\mathbf{x}_{i}^{T} \mathbf{u}+(\mathbf{u}^{T} \mathbf{x}_{i})(\mathbf{x}_{i}^{T} \mathbf{u})\mathbf{u}^{T}\mathbf{u} \right) \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\left\|\mathbf{x}_{i}\right\|^{2}-\mathbf{u}^{T} \mathbf{x}_{i}\mathbf{x}_{i}^{T} \mathbf{u} \right) \\ &=\frac{1}{n} \sum_{i=1}^{n}\left\|\mathbf{x}_{i}\right\|^{2}-\mathbf{u}^{T} \mathbf{\Sigma} \mathbf{u}\\ &= var(D)-\sigma_{\mathbf{u}}^{2} \end{aligned} \]

上式表明：\(var(D)=\sigma_{\mathbf{u}}^{2}+MSE\)

\(\mathbf{u}\) 的几何意义：\(\mathbb{R}^d\) 中使得数据沿其方向投影后方差最大的同时，MSE 最小的直线方向。

\(\mathbf{u}\) 被称为一阶主元（first principal component）

7.2.2 最佳2-维近似

（二阶主元分析：r=2）

假设 \(\mathbf{u}_1\) 已经找到，即 \(\mathbf{\Sigma}\) 的最大特征值对应的特征向量。

目标：寻找 \(\mathbf{u}_2\) ，简记为 \(\mathbf{v}\)，使得：\(\mathbf{v}^{T} \mathbf{u}_{1}=0,\mathbf{v}^{T} \mathbf{v} =1\)

考虑 \(\mathbf{x}_{i}\) 沿 \(\mathbf{v}\) 方向投影的方差：

\[\begin{array}{ll} \max\limits_{\mathbf{u}} & \sigma_{\mathbf{v}}^{2} = \mathbf{v}^{T} \mathbf{\Sigma} \mathbf{v} \\ \text{s.t} & \mathbf{v}^T\mathbf{v}-1=0\\ & \mathbf{v}^{T} \mathbf{u}_{1}=0 \end{array} \]

定义：\(J(\mathbf{v})=\mathbf{v}^{T} \mathbf{\Sigma} \mathbf{v}-\alpha\left(\mathbf{v}^{T} \mathbf{v}-1\right)-\beta\left(\mathbf{v}^{T} \mathbf{u}_{1}-0\right)\)

对 \(\mathbf{v}\) 求偏导得：

\[2 \Sigma \mathbf{v}-2 \alpha \mathbf{v}-\beta \mathbf{u}_{1}=\mathbf{0} \]

两边同乘 \(\mathbf{u}_{1}^{T}\)：

\[\begin{aligned} 2 \mathbf{u}_{1}^{T}\Sigma \mathbf{v}-2 \alpha \mathbf{u}_{1}^{T}\mathbf{v}-\beta \mathbf{u}_{1}^{T}\mathbf{u}_{1} &=0 \\ 2 \mathbf{u}_{1}^{T}\Sigma \mathbf{v}-\beta &= 0\\ 2 \mathbf{v}^{T}\Sigma \mathbf{u}_{1}-\beta &= 0\\ 2 \mathbf{v}^{T}\lambda_1 \mathbf{u}_{1}-\beta &= 0\\ \beta &= 0 \end{aligned} \]

再代入到原式：

\[2 \Sigma \mathbf{v}-2 \alpha \mathbf{v}=\mathbf{0}\\ \Sigma \mathbf{v}=\alpha \mathbf{v} \]

故 \(\mathbf{v}\) 也是 \(\mathbf{\Sigma}\) 的特征向量。

\(\sigma_{\mathbf{v}}^{2} = \mathbf{v}^{T} \mathbf{\Sigma} \mathbf{v} =\alpha\)，故 \(\alpha\) 应取 \(\mathbf{\Sigma}\) （第二大）的特征向量。

问题1：上述求得的 \(\mathbf{v}\) （即 \(\mathbf{u}_2\) ），与 \(\mathbf{u}_1\) 一起考虑，能否使 \(D\) 在 \(span\{\mathbf{u}_1, \mathbf{u}_2 \}\) 上投影总方差最大？

设 \(\mathbf{x}_i=\underbrace{a_{i1} \mathbf{u}_1+a_{i2}\mathbf{u}_2}_{投影}+\cdots\)

则 \(\mathbf{x}_i\) 在 \(span\{\mathbf{u}_1, \mathbf{u}_2 \}\) 上投影坐标：\(\mathbf{a}_{i}=(a_{i1},a_{i2})^T=(\mathbf{u}_1^{T}\mathbf{x}_i,\mathbf{u}_2^{T}\mathbf{x}_i)^{T}\)

令 \(\mathbf{U}_{2}=\left(\begin{array}{cc} \mid & \mid \\ \mathbf{u}_{1} & \mathbf{u}_{2} \\ \mid & \mid \end{array}\right)\)，则 \(\mathbf{a}_{i}=\mathbf{U}_{2}^{T} \mathbf{x}_{i}\)

投影总方差为：

\[\begin{aligned} \operatorname{var}(\mathbf{A}) &=\frac{1}{n} \sum_{i=1}^{n}\left\|\mathbf{a}_{i}-\mathbf{0}\right\|^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\mathbf{U}_{2}^{T} \mathbf{x}_{i}\right)^{T}\left(\mathbf{U}_{2}^{T} \mathbf{x}_{i}\right) \\ &=\frac{1}{n} \sum_{i=1}^{n} \mathbf{x}_{i}^{T}\left(\mathbf{U}_{2} \mathbf{U}_{2}^{T}\right) \mathbf{x}_{i}\\ &=\frac{1}{n} \sum_{i=1}^{n} \mathbf{x}_{i}^{T}\left( \mathbf{u}_{1}\mathbf{u}_{1}^T + \mathbf{u}_{2}\mathbf{u}_{2}^T \right) \mathbf{x}_{i}\\ &=\mathbf{u}_{1}^T\mathbf{\Sigma} \mathbf{u}_{1} + \mathbf{u}_{2}^T\mathbf{\Sigma} \mathbf{u}_{2}\\ &= \lambda_1 +\lambda_2 \end{aligned} \]

问题2：平均平方误差是否最小？

其中，\(\mathbf{x}_{i}^{\prime}=\mathbf{U}_{2}\mathbf{U}_{2}^{T} \mathbf{x}_{i}\)

\[\begin{aligned} M S E &= \frac{1}{n} \sum_{i=1}^{n}\left\|\mathbf{x}_{i}-\mathbf{x}_{i}^{\prime}\right\|^{2} \\ &= \frac{1}{n} \sum_{i=1}^{n}\left\|\mathbf{x}_{i}\right\|^{2} - \frac{1}{n} \sum_{i=1}^{n} \mathbf{x}_{i}^{T}\left(\mathbf{U}_{2} \mathbf{U}_{2}^{T}\right) \mathbf{x}_{i}\\ &= var(D) - \lambda_1 - \lambda_2 \end{aligned} \]

结论：

1. \(\mathbf{\Sigma}\) 的前 \(r\) 个特征值的和 \(\lambda_1+\cdots+\lambda_r(\lambda_1\ge\cdots\ge\lambda_r)\) 给出最大投影总方差；
2. \(var(D)-\sum\limits_{i=1}^r \lambda_i\) 给出最小MSE；
3. \(\lambda_1,\cdots,\lambda_r\) 相应的特征向量 \(\mathbf{u}_{1},\cdots\mathbf{u}_{r}\) 张成 \(r\) - 阶主元。

7.2.3 推广

\(\Sigma_{d\times d}\) ，\(\lambda_1 \ge \lambda_2 \ge \cdots \lambda_d\)，中心化

\(\sum\limits_{i=1}^r\lambda_i\)：最大投影总方差；

\(var(D)-\sum\limits_{i=1}^r\lambda_i\)：最小MSE

实践： 如何选取适当的 \(r\)，考虑比值 \(\frac{\sum\limits_{i=1}^r\lambda_i}{var(D)}\) 与给定阈值 \(\alpha\) 比较

算法 7.1 PCA：

输入：\(D\)，\(\alpha\)

输出：\(A\) (降维后)

1. \(\boldsymbol{\mu} = \frac{1}{n}\sum\limits_{i=1}^r\mathbf{x}_i\);
2. \(\mathbf{Z}=\mathbf{D}-\mathbf{1}\cdot \boldsymbol{\mu} ^T\);
3. \(\mathbf{\Sigma}=\frac{1}{n}(\mathbf{Z}^T\mathbf{Z})\);
4. \(\lambda_1 \ge \lambda_2 \ge \cdots \lambda_d\)，\(\longleftarrow \mathbf{\Sigma}\) 的特征值（降序排列）;
5. \(\mathbf{u}_1,\mathbf{u}_2,\cdots,\mathbf{u}_d\)，\(\longleftarrow \mathbf{\Sigma}\) 的特征向量（单位正交）；
6. 计算 \(\frac{\sum\limits_{i=1}^r\lambda_i}{var(D)}\)，选取其比值超过 \(\alpha\) 最小的 \(r\)；
7. \(\mathbf{U}_r=(\mathbf{u}_1,\mathbf{u}_2,\cdots,\mathbf{u}_r)\);
8. \(A=\{\mathbf{a}_i|\mathbf{a}_i=\mathbf{U}_r^T\mathbf{x}_i, i=1,\cdots,n\}\)。

7.2.3 Kernel PCA：核主元分析

\(\phi:\mathcal{I}\to \mathcal{F}\subseteq \mathbb{R}^d\)

\(K:\mathcal{I}\times\mathcal{I}\to \mathbb{R}\)

\(K(\mathbf{x}_i,\mathbf{x}_j)=\phi^T(\mathbf{x}_i)\phi(\mathbf{x}_j)\)

已知：\(\mathbf{K}=[K(\mathbf{x}_i,\mathbf{x}_j)]_{n\times n}\)，\(\mathbf{\Sigma}_{\phi}=\frac{1}{n}\sum\limits_{i=1}^n\phi(\mathbf{x}_i)\phi(\mathbf{x}_i)^T\)

对象：\(\phi(\mathbf{x}_1),\phi(\mathbf{x}_2),\cdots,\phi(\mathbf{x}_n)\in \mathbb{R}^d\)，假设 \(\frac{1}{n}\sum\limits_{i}^{n}\phi(\mathbf{x}_i)=\mathbf{0}\)，\(\mathbf{K} \to \hat{\mathbf{K}}\)，已经中心化；

目标：\(\mathbf{u},\lambda,s.t. \mathbf{\Sigma}_{\phi}\mathbf{u}=\lambda\mathbf{u}\)

\[\begin{aligned} \frac{1}{n}\sum\limits_{i=1}^n\phi(\mathbf{x}_i)[\phi(\mathbf{x}_i)^T\mathbf{u}] &=\lambda\mathbf{u}\\ \sum\limits_{i=1}^n[\frac{\phi(\mathbf{x}_i)^T\mathbf{u}}{n\lambda}] \phi(\mathbf{x}_i)&=\mathbf{u}\\ \end{aligned} \]

相同于所有数据线性组合。

令：\(c_i=\frac{\phi(\mathbf{x}_i)^T\mathbf{u}}{n\lambda}\)，则 \(\mathbf{u}=\sum\limits_{i=1}^nc_i \phi(\mathbf{x}_i)\)。代入原式：

\[\begin{aligned} \left(\frac{1}{n} \sum_{i=1}^{n} \phi\left(\mathbf{x}_{i}\right) \phi\left(\mathbf{x}_{i}\right)^{T}\right)\left(\sum_{j=1}^{n} c_{j} \phi\left(\mathbf{x}_{j}\right)\right) &=\lambda \sum_{i=1}^{n} c_{i} \phi\left(\mathbf{x}_{i}\right) \\ \frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{n} c_{j} \phi\left(\mathbf{x}_{i}\right) \phi\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) &=\lambda \sum_{i=1}^{n} c_{i} \phi\left(\mathbf{x}_{i}\right) \\ \sum_{i=1}^{n}\left(\phi\left(\mathbf{x}_{i}\right) \sum_{j=1}^{n} c_{j} K(\mathbf{x}_i, \mathbf{x}_j) \right) &=n \lambda \sum_{i=1}^{n} c_{i} \phi\left(\mathbf{x}_{i}\right) \end{aligned} \]

注意，此处 \(\mathbf{K}=\hat{\mathbf{K}}\) 已经中心化

对于 \(\forall k (1\le k\le n)\)，两边同时左乘 \(\phi(\mathbf{x}_{k})\)：

\[\begin{aligned} \sum_{i=1}^{n}\left(\phi^T(\mathbf{x}_{k}) \phi\left(\mathbf{x}_{i}\right) \sum_{j=1}^{n} c_{j} K(\mathbf{x}_i, \mathbf{x}_j) \right) &=n \lambda \sum_{i=1}^{n} c_{i} \phi^T(\mathbf{x}_{k}) \phi\left(\mathbf{x}_{i}\right) \\ \sum_{i=1}^{n}\left(K(\mathbf{x}_k, \mathbf{x}_i) \sum_{j=1}^{n} c_{j} K(\mathbf{x}_i, \mathbf{x}_j) \right) &=n \lambda \sum_{i=1}^{n} c_{i} K(\mathbf{x}_k, \mathbf{x}_i) \\ \end{aligned} \]

令 \(\mathbf{K}_{i}=\left(K\left(\mathbf{x}_{i}, \mathbf{x}_{1}\right), K\left(\mathbf{x}_{i}, \mathbf{x}_{2}\right), \cdots, K\left(\mathbf{x}_{i}, \mathbf{x}_{n}\right)\right)^{T}\) (核矩阵的第 \(i\) 行，\(\mathbf{K}=(\begin{bmatrix} \mathbf{K}_1^T \\ \vdots \\ \mathbf{K}_n^T \end{bmatrix})\))，\(\mathbf{c}=(c_1,c_2,\cdots,c_n)^T\)，则：

\[\begin{aligned} \sum_{i=1}^{n}K(\mathbf{x}_k, \mathbf{x}_i) \mathbf{K}^T_i\mathbf{c} &=n \lambda \mathbf{K}^T_k\mathbf{c},k=1,2,\cdots,n \\ \mathbf{K}^T_k\begin{bmatrix} \mathbf{K}_1^T \\ \vdots \\ \mathbf{K}_n^T \end{bmatrix}\mathbf{c} &=n \lambda \mathbf{K}^T_k\mathbf{c}\\ \mathbf{K}^T_k\mathbf{K} &=n \lambda \mathbf{K}^T_k\mathbf{c} \end{aligned} \]

即 \(\mathbf{K}^2\mathbf{c}=n\lambda \mathbf{K}\mathbf{c}\)

假设 \(\mathbf{K}^{-1}\) 存在

\[\begin{aligned} \mathbf{K}^2\mathbf{c}&=n\lambda \mathbf{K}\mathbf{c}\\ \mathbf{K}\mathbf{c}&=n\lambda \mathbf{c}\\ \mathbf{K}\mathbf{c}&= \eta\mathbf{c},\eta=n\lambda \end{aligned} \]

结论：\(\frac{\eta_1}{n}\ge\frac{\eta_2}{n}\ge\cdots\ge\frac{\eta_n}{n}\)，给出在特征空间中 \(\phi(\mathbf{x}_1),\phi(\mathbf{x}_2),\cdots,\phi(\mathbf{x}_n)\) 的投影方差：\(\sum\limits_{i=1}^{r}\frac{\eta_r}{n}\)，其中 \(\eta_1\ge\eta_2\cdots\ge\eta_n\) 是 \(\mathbf{K}\) 的特征值。

问：可否计算出 \(\phi(\mathbf{x}_1),\phi(\mathbf{x}_2),\cdots,\phi(\mathbf{x}_n)\) 在主元方向上的投影（即降维之后的数据）？

设 \(\mathbf{u}_1,\cdots,\mathbf{u}_d\) 是 \(\mathbf{\Sigma}_{\phi}\) 的特征向量，则 \(\phi(\mathbf{x}_j)=a_1\mathbf{u}_1+\cdots+a_d\mathbf{u}_d\)，其中

\[\begin{aligned} a_k &= \phi(\mathbf{x}_j)^T\mathbf{u}_k, k=1,2,\cdots,d\\ &= \phi(\mathbf{x}_j)^T\sum\limits_{i=1}^nc_{ki} \phi(\mathbf{x}_i)\\ &= \sum\limits_{i=1}^nc_{ki} \phi(\mathbf{x}_j)^T\phi(\mathbf{x}_i)\\ &= \sum\limits_{i=1}^nc_{ki} K(\mathbf{x}_j,\mathbf{x}_i) \end{aligned} \]

算法7.2：核主元分析（\(\mathcal{F}\subseteq \mathbb{R}^d\)）

输入：\(K\)，\(\alpha\)

输出：\(A\) （降维后数据的投影坐标）

1. \(\hat{\mathbf{K}} :=\left(\mathbf{I}-\frac{1}{n} \mathbf{1}_{n \times n}\right) \mathbf{K}\left(\mathbf{I}-\frac{1}{n} \mathbf{1}_{n \times n}\right)\)

2. \(\eta_1,\eta_2,\cdots\eta_d\) \(\longleftarrow \mathbf{K}\) 的特征值，只取前 \(d\) 个

3. \(\mathbf{c}_1,\mathbf{c}_2,\cdots,\mathbf{c}_d\)\(\longleftarrow \mathbf{K}\) 的特征向量（单位化，正交）

4. \(\mathbf{c}_i \leftarrow \frac{1}{\sqrt{\eta_i}}\cdot \mathbf{c}_i,i=1,\cdots,d\)

5. 选取最小的 \(r\) 使得：\(\frac{\sum\limits_{i=1}^r\frac{\eta_i}{n}}{\sum\limits_{i=1}^d\frac{\eta_i}{n}}\ge \alpha\)

6. \(\mathbf{C}_r=(\mathbf{c}_1,\mathbf{c}_2,\cdots,\mathbf{c}_r)\)

7. \(A=\{\mathbf{a}_i|\mathbf{a}_i=\mathbf{C}_r^T\mathbf{K}_i, i=1,\cdots,n\}\)

Chapter 14：Hierarchical Clustering 分层聚类

14.1 预备

Def.1 给定数据集 \(\mathbf{D}=\{ \mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\},(\mathbf{x}_i\in \mathbb{R}^d)\)，\(\mathbf{D}\) 的一个聚类是指 \(\mathbf{D}\) 的划分 \(\mathcal{C}=\{C_1,C_2,\cdots,C_k \}\) s.t. \(C_i\subseteq \mathbf{D},C_i \cap C_j=\emptyset, \cup_{i=1}^k C_i=\mathbf{D}\)；

称聚类 \(\mathcal{A}=\{A_1,\cdots,A_r\}\) 是聚类 \(\mathcal{B}=\{B_1,\cdots,B_s\}\) 的嵌套，如果 \(r>s\)，且对于 \(\forall A_i \in \mathcal{A}\) ，存在 \(B_j \in \mathcal{B}\) 使得 \(A_i \subseteq B_j\)

\(\mathbf{D}\) 的分层聚类是指一个嵌套聚类序列 \(\mathcal{C}_1,\cdots,\mathcal{C}_n\)，其中 \(\mathcal{C}_1=\{ \{\mathbf{x}_1\},\{\mathbf{x}_2\},\cdots,\{\mathbf{x}_n\}\},\cdots,\mathcal{C}_n=\{\{ \mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\} \}\)，且 \(\mathcal{C}_t\) 是 \(\mathcal{C}_{t+1}\) 的嵌套。

Def.2 分层聚类示图的顶点集是指所有在 \(\mathcal{C}_1,\cdots,\mathcal{C}_n\) 中出现的元，如果 \(C_i \in \mathcal{C}_t\) 且 \(C_j \in \mathcal{C}_{t+1}\) 满足，则 \(C_i\) 与 \(C_j\) 之间有一条边。

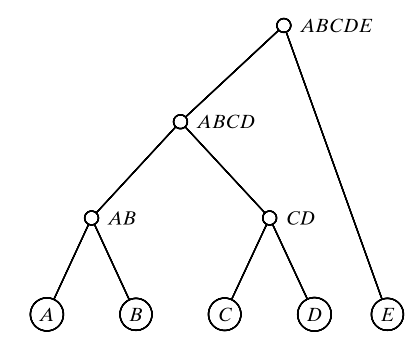
事实：

1. 分层聚类示图是一棵二叉树（不一定，作为假设，假设每层只聚两类），分层聚类与其示图一一对应。
2. 设（即数据点数为 \(n\)），则所有可能的分层聚类示图数目为 \((2n-3)!!\) （跃乘 \(1\times 3 \times 5 \times \cdots\)）

14.2 团聚分层聚类

算法14.1 ：

输入： \(\mathbf{D}, k\)

输出：\(\mathcal{C}\)

1. \(\mathcal{C} \leftarrow \{C_i=\{\mathbf{x}_i\}|\mathbf{x}_i \in \mathbf{D} \}\)
2. \(\Delta \leftarrow \{\delta(\mathbf{x}_i,\mathbf{x}_j):\mathbf{x}_i,\mathbf{x}_j \in \mathbf{D} \}\)
3. repeat
4. ​ 寻找最近的对 \(C_i,C_j \in \mathcal{C}\)
5. ​ \(C_{ij}\leftarrow C_i \cup C_j\)
6. ​ \(\mathcal{C}\leftarrow (\mathcal{C} | \{C_i,C_j \}) \cup {C_{ij}}\)
7. ​ 根据 \(\mathcal{C}\) 更新距离矩阵 \(\Delta\)
8. Until \(|\mathcal{C}|=k\)

问题：如何定义/计算 \(C_i,C_j\) 的距离，即 \(\delta(C_i,C_j)\) ?

\(\delta(C_i,C_j)\) 有以下五种不同方式：

1. 简单连接：\(\delta(C_i,C_j):= \min \{\delta(\mathbf{x},\mathbf{y}) | \mathbf{x} \in C_i, \mathbf{y} \in C_j\}\)

2. 完全连接：\(\delta(C_i,C_j):= \max \{\delta(\mathbf{x},\mathbf{y}) | \mathbf{x} \in C_i, \mathbf{y} \in C_j\}\)

3. 组群平均：\(\delta(C_i,C_j):= \frac{\sum\limits_{\mathbf{x} \in C_i}\sum\limits_{\mathbf{y} \in C_j}\delta(\mathbf{x},\mathbf{y})}{n_i \cdot n_j}, n_i=|C_i|,n_j=|C_j|\)

4. 均值距离：\(\delta(C_i,C_j):= ||\boldsymbol{\mu}_i-\boldsymbol{\mu}_j|| ^2,\boldsymbol{\mu}_i=\frac{1}{n}\sum\limits_{\mathbf{x} \in C_i}\mathbf{x},\boldsymbol{\mu}_j=\frac{1}{n}\sum\limits_{\mathbf{y} \in C_j}\mathbf{y}\)

5. 极小方差：对任意 \(C_i\)，定义平方误差和 \(SSE_i= \sum\limits_{\mathbf{x} \in C_i} ||\mathbf{x}-\boldsymbol{\mu}_i|| ^2\)

   对 \(C_i,C_j,SSE_{ij}:=\sum\limits_{\mathbf{x} \in C_i\cup C_j} ||\mathbf{x}-\boldsymbol{\mu}_{ij}|| ^2\)，其中 \(\boldsymbol{\mu}_{ij}:=\frac{1}{n_i+n_j}\sum\limits_{\mathbf{x} \in C_i\cup C_j}\mathbf{x}\)

   \(\delta(C_i,C_j):=SSE_{ij}-SSE_i-SSE_j\)

证明：\(\delta(C_i,C_j)=\frac{n_in_j}{n_i+n_j}||\boldsymbol{\mu}_i-\boldsymbol{\mu}_j|| ^2\)

简记：\(C_{ij}:=C_i\cup C_j,n_{ij}:=n_i+n_j\)

注意：\(C_i \cap C_j=\emptyset\)，故 \(|C_{ij}|=n_i+n_j\)

\[\begin{aligned} \delta\left(C_{i}, C_{j}\right) &=\sum_{\mathbf{z} \in C_{i j}}\left\|\mathbf{z}-\boldsymbol{\mu}_{i j}\right\|^{2}-\sum_{\mathbf{x} \in C_{i}}\left\|\mathbf{x}-\boldsymbol{\mu}_{i}\right\|^{2}-\sum_{\mathbf{y} \in C_{j}}\left\|\mathbf{y}-\boldsymbol{\mu}_{j}\right\|^{2} \\ &=\sum_{\mathbf{z} \in C_{i j}} \mathbf{z}^{T} \mathbf{z}-n_{i j} \boldsymbol{\mu}_{i j}^{T} \boldsymbol{\mu}_{i j}-\sum_{\mathbf{x} \in C_{i}} \mathbf{x}^{T} \mathbf{x}+n_{i} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}-\sum_{\mathbf{y} \in C_{j}} \mathbf{y}^{T} \mathbf{y}+n_{j} \boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j} \\ &=n_{i} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}+n_{j} \boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j}-\left(n_{i}+n_{j}\right) \boldsymbol{\mu}_{i j}^{T} \boldsymbol{\mu}_{i j} \end{aligned} \]

注意到：\(\boldsymbol{\mu}_{i j}=\frac{1}{n_{ij}}\sum\limits_{\mathbf{z} \in C_{ij}} \mathbf{z}=\frac{1}{n_i+n_j}(\sum\limits_{\mathbf{x} \in C_{i}} \mathbf{x}+\sum\limits_{\mathbf{y} \in C_{j}} \mathbf{y})=\frac{1}{n_i+n_j}(n_i\boldsymbol{\mu}_{i}+n_j\boldsymbol{\mu}_{j})\)

故：\(\boldsymbol{\mu}_{i j}^{T} \boldsymbol{\mu}_{i j}=\frac{1}{\left(n_{i}+n_{j}\right)^{2}}\left(n_{i}^{2} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}+2 n_{i} n_{j} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{j}+n_{j}^{2} \boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j}\right)\)

\[\begin{aligned} \delta\left(C_{i}, C_{j}\right) &=n_{i} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}+n_{j} \mu_{j}^{T} \boldsymbol{\mu}_{j}-\frac{1}{\left(n_{i}+n_{j}\right)}\left(n_{i}^{2} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}+2 n_{i} n_{j} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{j}+n_{j}^{2} \boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j}\right) \\ &=\frac{n_{i}\left(n_{i}+n_{j}\right) \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}+n_{j}\left(n_{i}+n_{j}\right) \boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j}-n_{i}^{2} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}-2 n_{i} n_{j} \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{j}-n_{j}^{2} \boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j}}{n_{i}+n_{j}} \\ &=\frac{n_{i} n_{j}\left(\boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{i}-2 \boldsymbol{\mu}_{i}^{T} \boldsymbol{\mu}_{j}+\boldsymbol{\mu}_{j}^{T} \boldsymbol{\mu}_{j}\right)}{n_{i}+n_{j}} \\ &=\left(\frac{n_{i} n_{j}}{n_{i}+n_{j}}\right)\left\|\boldsymbol{\mu}_{i}-\boldsymbol{\mu}_{j}\right\|^{2} \end{aligned} \]

问题：如何快速计算算法14.1 第7步：更新矩阵？

☆ Lance–Williams formula

\[\begin{array}{r} \delta\left(C_{i j}, C_{r}\right)=\alpha_{i} \cdot \delta\left(C_{i}, C_{r}\right)+\alpha_{j} \cdot \delta\left(C_{j}, C_{r}\right)+ \\ \beta \cdot \delta\left(C_{i}, C_{j}\right)+\gamma \cdot\left|\delta\left(C_{i}, C_{r}\right)-\delta\left(C_{j}, C_{r}\right)\right| \end{array} \]

Measure	\(\alpha_i\)	\(\alpha_j\)	\(\beta\)	\(\gamma\)
简单连接	\(1\over2\)	\(1\over2\)	\(0\)	\(-{1\over2}\)
完全连接	\(1\over2\)	\(1\over2\)	\(0\)	\(1\over2\)
组群平均	\(\frac{n_i}{n_i+n_j}\)	\(\frac{n_j}{n_i+n_j}\)	\(0\)	\(0\)
均值距离	\(\frac{n_i}{n_i+n_j}\)	\(\frac{n_j}{n_i+n_j}\)	\(\frac{-n_in_j}{(n_i+n_j)^2}\)	\(0\)
极小方差	\(\frac{n_i+n_r}{n_i+n_j+n_r}\)	\(\frac{n_j+n_r}{n_i+n_j+n_r}\)	\(\frac{-n_r}{n_i+n_j+n_r}\)	\(0\)

Proof:

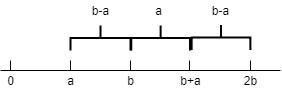
1. 简单连接
   \[\begin{aligned} \delta\left(C_{i j}, C_{r}\right) &= \min \{\delta({\mathbf{x}, \mathbf{y}} )|\mathbf{x}\in C_{ij}, \mathbf{y} \in C_r\} \\ &= \min \{\delta({C_{i}, C_{r}), \delta(C_{j}, C_{r}} )\} \end{aligned}\\ a=\frac{a+b-|a-b|}{2},b=\frac{a+b+|a-b|}{2} \]

2. 完全连接

   见上图

3. 组群平均

   \[\begin{aligned} \delta\left(C_{i j}, C_{r}\right) &= \frac{\sum\limits_{\mathbf{x} \in C_i\cup C_j}\sum\limits_{\mathbf{y} \in C_r}\delta(\mathbf{x},\mathbf{y})}{(n_i+n_j )\cdot n_r} \\ &= \frac{\sum\limits_{\mathbf{x} \in C_i}\sum\limits_{\mathbf{y} \in C_r}\delta(\mathbf{x},\mathbf{y})+\sum\limits_{\mathbf{x} \in C_j}\sum\limits_{\mathbf{y} \in C_r}\delta(\mathbf{x},\mathbf{y})}{(n_i+n_j )\cdot n_r} \\ &=\frac{n_in_r\delta(C_i,C_r)+n_jn_r\delta(C_j,C_r)}{(n_i+n_j )\cdot n_r}\\ &=\frac{n_i\delta(C_i,C_r)+n_j\delta(C_j,C_r)}{(n_i+n_j )} \end{aligned} \]

4. 均值距离：作业

5. 极小方差

   基于均值距离的结论再代入 \(\delta(C_i,C_j)=\frac{n_in_j}{n_i+n_j}||\boldsymbol{\mu}_i-\boldsymbol{\mu}_j|| ^2\)

事实：算法14.1 的复杂度为 \(O(n^2\log n)\)

Chapter 15：基于密度的聚类

适用数据类型：非凸，又称非凸聚类；K-means 适用于凸数据

15.1 DBSCAN 算法

• 定义记号：\(\forall \mathbf{x}\in \mathbb{R}^d,N_{\epsilon}(\mathbf{x}):=\{\mathbf{y}\in \mathbb{R}^d|\delta(\mathbf{x}-\mathbf{y})\le\epsilon \}\)，其中 \(\delta(\mathbf{x}-\mathbf{y})=||\mathbf{x}-\mathbf{y}||\) 欧式距离，其他距离也可。\(\mathbf{D}\subseteq \mathbb{R}^d\)

Def.1 设 \(minpts \in \mathbb{N}_+\) 是用户定义的局部密度，如果 \(|N_{\epsilon}(\mathbf{x})\cap\mathbf{D}|\ge minpts\) ，则称 \(\mathbf{x}\) 是 \(\mathbf{D}\) 核心点；如果 \(|N_{\epsilon}(\mathbf{x})\cap\mathbf{D}|< minpts\) ，且 \(\mathbf{x}\in N_{\epsilon}(\mathbf{z})\) ，其中 \(\mathbf{z}\) 是 \(\mathbf{D}\) 的核心点，则称 \(\mathbf{x}\) 是 \(\mathbf{D}\) 的边缘点；如果 \(\mathbf{x}\) 既不是核心点又不是边缘点，则称 \(\mathbf{x}\) 是 \(\mathbf{D}\) 的噪点。

Def.2 如果 \(\mathbf{x}\in N_{\epsilon}(\mathbf{y})\) 且 \(\mathbf{y}\) 是核心点，则称 \(\mathbf{x}\) 到 \(\mathbf{y}\) 是直接密度可达的。如果存在点列 \(\mathbf{x}_0,\mathbf{x}_1,\cdots,\mathbf{x}_l\)，使得 \(\mathbf{x}_0=\mathbf{x},\mathbf{x}_l=\mathbf{y}\)，且 \(\mathbf{x}_{i}\) 到 \(\mathbf{x}_{i-1}\) 是直接密度可达，则称 \(\mathbf{x}\) 到 \(\mathbf{y}\) 是密度可达。

Def.3 如果存在 \(\mathbf{z}\in \mathbf{D}\)，使得 \(\mathbf{x}\) 和 \(\mathbf{y}\) 到 \(\mathbf{z}\) 都是密度可达的，称 \(\mathbf{x}\) 和 \(\mathbf{y}\) 是密度连通的。

Def.4 基于密度的聚类是指基数最大的密度连通集（即集合内任意两点都是密度连通）。

算法15.1 ： DBSCAN (\(O(n^2)\))

输入： \(\mathbf{D}, \epsilon, minpts\)

输出：\(\mathcal{C},Core,Border,Noise\)

1. \(Core \leftarrow \emptyset\)

2. 对每一个 \(\mathbf{x}_i\in \mathbf{D}\)

   2.1 计算 \(N_\epsilon(\mathbf{x}_i)(\subseteq \mathbf{D})\)

   2.2 \(id(\mathbf{x}_i)\leftarrow \emptyset\)

   2.3 如果 \(N_\epsilon(\mathbf{x}_i)\ge minpts\)，则 \(Core\leftarrow Core \cup \{ \mathbf{x}_i\}\)

3. \(k\leftarrow 0\)

4. 对每一个 \(\mathbf{x}_i\in Core, s.t.id(\mathbf{x}_i)= \emptyset\)，执行

   4.1 \(k\leftarrow k+1\)

   4.2 \(id(\mathbf{x}_i)\leftarrow k\)

   4.3 \(Density Connected (\mathbf{x}_i,k)\)

5. \(\mathcal{C}\leftarrow \{ C_i\}_{i=1}^k\)，其中 \(C_i\leftarrow \{\mathbf{x}_i \in \mathbf{D} |id(\mathbf{x}_i)=i\}\)

6. \(Noise \leftarrow \{\mathbf{x}_i \in \mathbf{D} |id(\mathbf{x}_i)=\emptyset\}\)

7. \(Border\leftarrow \mathbf{D}\setminus \{Core\cup Noise \}\)

8. return \(\mathcal{C},Core,Border,Noise\)

\(Density Connected (\mathbf{x}_i,k)\)：

1. 对于每一个 \(\mathbf{y} \in N_\epsilon(\mathbf{x}) \setminus {\mathbf{x}}\)

   1.1 \(id(\mathbf{y})\leftarrow k\)

   1.2 如果 \(\mathbf{y}\in Core\)，则 \(Density Connected (\mathbf{y},k)\)

Remark：DBSCAN 对 \(\varepsilon\) 敏感：\(\varepsilon\) 过小，稀疏的类可能被认作噪点；\(\varepsilon\) 过大，稠密的类可能无法区分。

15.2 密度估计函数（DEF）

\(\forall \mathbf{z}\in \mathbb{R}^d\)，定义 \(K(\mathbf{z})=\frac{1}{(2\pi)^{d/2}}e^{-\frac{\mathbf{z}^T\mathbf{z}}{2}}\)，\(\forall \mathbf{x}\in \mathbb{R}^d,\hat{f}(\mathbf{x}):=\frac{1}{nh^d}\sum\limits_{i=1}^{n}K(\frac{\mathbf{x}-\mathbf{x}_i}{h})\)

其中 \(h>0\) 是用户指定的步长，\(\{\mathbf{x}_1,\cdots,\mathbf{x}_n\}\) 是给定的数据集

15.3 DENCLUE

Def.1 称 \(\mathbf{x}^*\in \mathbb{R}^d\) 是密度吸引子，如果它决定概率密度函数 \(f\) 的一个局部最大值。（PDF一般未知）

称 \(\mathbf{x}^*\in \mathbb{R}^d\) 是 \(\mathbf{x}\in \mathbb{R}^d\) 的密度吸引子，如果存在 \(\mathbf{x}_0,\mathbf{x}_1,\dots,\mathbf{x}_m\)，使得 \(\mathbf{x}_0=\mathbf{x},||\mathbf{x}_m-\mathbf{x}^*||\le\epsilon\)，且 \(\mathbf{x}_{t+1}=\mathbf{x}_{t}+\delta \cdot \nabla \hat{f}(\mathbf{x}_{t})\quad (1)\)

其中 \(\epsilon,\delta >0\) 是用户定义的误差及步长，\(\hat{f}\) 是DEF。

• 更高效的迭代公式：

动机：当 \(\mathbf{x}\) 靠近 \(\mathbf{x}^*\) 时，迭代公式（1）迭代效率低 \(\nabla \hat{f}(\mathbf{x}^*)=0\)

而 \(\nabla \hat{f}(\mathbf{x})=\frac{\partial}{\partial \mathbf{x}} \hat{f}(\mathbf{x})=\frac{1}{n h^{d}} \sum\limits_{i=1}^{n} \frac{\partial}{\partial \mathbf{x}} K\left(\frac{\mathbf{x}-\mathbf{x}_{i}}{h}\right)\)

\(\begin{aligned} \frac{\partial}{\partial \mathbf{x}} K(\mathbf{z}) &=\left(\frac{1}{(2 \pi)^{d / 2}} \exp \left\{-\frac{\mathbf{z}^{T} \mathbf{z}}{2}\right\}\right) \cdot-\mathbf{z} \cdot \frac{\partial \mathbf{z}}{\partial \mathbf{x}} \\ &=K(\mathbf{z}) \cdot-\mathbf{z} \cdot \frac{\partial \mathbf{z}}{\partial \mathbf{x}} \end{aligned}\)

将 \(\mathbf{z}=\frac{\mathbf{x}-\mathbf{x}_i}{h}\) 代入得：\(\frac{\partial}{\partial \mathbf{x}} K\left(\frac{\mathbf{x}-\mathbf{x}_{i}}{h}\right)=K\left(\frac{\mathbf{x}-\mathbf{x}_{i}}{h}\right) \cdot\left(\frac{\mathbf{x}_{i}-\mathbf{x}}{h}\right) \cdot\left(\frac{1}{h}\right)\)

故有：\(\nabla \hat{f}(\mathbf{x})=\frac{1}{n h^{d+2}} \sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}-\mathbf{x}_{i}}{h}\right) \cdot\left(\mathbf{x}_{i}-\mathbf{x}\right)\)

则：\(\frac{1}{n h^{d+2}} \sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}^*-\mathbf{x}_{i}}{h}\right) \cdot\left(\mathbf{x}_{i}-\mathbf{x}^*\right)=0\)

故有：\(\mathbf{x}^*=\frac{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}^*-\mathbf{x}_{i}}{h}\right)\cdot \mathbf{x}_{i}}{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}^*-\mathbf{x}_{i}}{h}\right)}\quad (2)\)

由（1）：\(\mathbf{x}_{t+1}-\mathbf{x}_{t}=\delta \cdot \nabla \hat{f}(\mathbf{x}_{t})\)，（靠近 \(\mathbf{x}^*\) 时）近似有：\(\mathbf{x}_{t+1}-\mathbf{x}_{t}\approx0\)

且：\(\mathbf{x}_t=\frac{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}_t-\mathbf{x}_{i}}{h}\right)\cdot \mathbf{x}_{i}}{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}_t-\mathbf{x}_{i}}{h}\right)}\)

故：\(\mathbf{x}_{t+1}=\frac{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}_t-\mathbf{x}_{i}}{h}\right)\cdot \mathbf{x}_{i}}{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}_t-\mathbf{x}_{i}}{h}\right)}\)

Def.2 称 \(C\subseteq \mathbf{D}\) 是基于密度的类，如果存在密度吸引子 \(\mathbf{x}^*_1,\dots,\mathbf{x}^*_m\) \(s.t:\)

1. \(\forall \mathbf{x}\in C\) 都有某个 \(\mathbf{x}^*_i\) 使得， \(\mathbf{x}^*_i\) 是 \(\mathbf{x}\) 的密度吸引子；
2. \(\forall i,\hat{f}(\mathbf{x}^*_i)\ge \xi\)，其中 \(\xi\) 是用户指定的极小密度阈值；
3. \(\forall\mathbf{x}^*_i,\mathbf{x}^*_j\) 都密度可达，即存在路径从 \(\mathbf{x}^*_i\) 到 \(\mathbf{x}^*_j\) 使得路径上所有点 \(\mathbf{y}\) 都有 \(\hat{f}(\mathbf{y})\ge\xi\)。

算法15.2 ： DENCLUE 算法

输入：\(\mathbf{D},h,\xi,\epsilon\)

输出：\(\mathcal{C}\) （基于密度的聚类）

1. \(\mathcal{A}\leftarrow\emptyset\)

2. 对每一个 \(\mathbf{x}\in \mathbf{D}\):

   2.1 \(\mathbf{x}^* \leftarrow FINDATTRACTOR(\mathbf{x},\mathbf{D},h,\xi,\epsilon)\)

   2.2 \(R(\mathbf{x}^*)\leftarrow\emptyset\)

   2.3 if \(\hat{f}(\mathbf{x}^*)\ge \xi\) then:

   2.4 \(\mathcal{A}\leftarrow \mathcal{A}\cup\{ \mathbf{x}^*\}\)

   2.5 \(R(\mathbf{x}^*)\leftarrow R(\mathbf{x}^*)\cup\{ \mathbf{x}^* \}\)

3. \(\mathcal{C}\leftarrow\{\text{maximal}\ C \subseteq \mathcal{A}| \forall\mathbf{x}^*_i,\mathbf{x}^*_j \in C, 满足 Def \ 2 条件3 \}\)

4. \(\forall C \in \mathcal{C}:\)

   4.1 对每一个 \(\mathbf{x}^*\in C\)，令 \(C\leftarrow C\cup R(\mathbf{x}^*)\)

5. Return \(\mathcal{C}\)

\(FINDATTRACTOR(\mathbf{x},\mathbf{D},h,\xi,\epsilon)\):

1. \(t\leftarrow 0\)

2. \(\mathbf{x}_{t}=\mathbf{x}\)

3. Repeat:

   \(\mathbf{x}_{t+1}\leftarrow\frac{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}_t-\mathbf{x}_{i}}{h}\right)\cdot \mathbf{x}_{i}}{\sum\limits_{i=1}^{n} K\left(\frac{\mathbf{x}_t-\mathbf{x}_{i}}{h}\right)}\)

   \(t\leftarrow t+1\)

4. Until \(||\mathbf{x}_{t}-\mathbf{x}_{t-1}||<\epsilon\)

Chapter 20: Linear Discriminant Analysis

Set up：\(\mathbf{D}=\{(\mathbf{x}_i,y_i) \}_{i=1}^n\)， 其中 \(y_i=1,2\)（或 \(\pm 1\) 等），\(\mathbf{D}_1=\{\mathbf{x}_i|y_i=1 \}\)，\(\mathbf{D}_2=\{\mathbf{x}_i|y_i=2 \}\)

Goal：寻找向量 \(\mathbf{w}\in \mathbb{R}^d\) （代表直线方向）使得 \(\mathbf{D}_1,\mathbf{D}_2\) 的“平均值”距离最大且“总方差”最小。

20.1 Normal LDA

设 \(\mathbf{w} \in \mathbb{R}^d,\mathbf{w}^T\mathbf{w}=1\)，则 \(\mathbf{x}_i\) 在 \(\mathbf{w}\) 方向上的投影为 \(\mathbf{x}_{i}^{\prime}=\left(\frac{\mathbf{w}^{T} \mathbf{x}_{i}}{\mathbf{w}^{T} \mathbf{u}}\right) \mathbf{w}=a_{i} \mathbf{w},a_{i}=\mathbf{w}^{T} \mathbf{x}_{i}\)

则 \(\mathbf{D}_1\) 中数据在 \(\mathbf{w}\) 上的投影平均值为：（\(|\mathbf{D}_1|=n_1\)）

\[m_1:=\frac{1}{n_1}\sum\limits_{\mathbf{x}_i\in \mathbf{D}_1}a_i=\boldsymbol{\mu}_1^T\mathbf{w} \]

投影平均值等于平均值的投影。

类似地： \(\mathbf{D}_2\) 中数据在 \(\mathbf{w}\) 上的投影平均值为：

\[m_2:=\frac{1}{n_2}\sum\limits_{\mathbf{x}_i\in \mathbf{D}_2}a_i=\boldsymbol{\mu}_2^T\mathbf{w} \]

目标之一：寻找 \(\mathbf{w}\) 使得 \((m_1-m_2)^2\) 最大。

对于 \(\mathbf{D}_i\)，定义：

\[s_i^2=\sum\limits_{\mathbf{x}_k\in \mathbf{D}_i}(a_k-m_i)^2 \]

注意：\(s_i^2=n_i\sigma^2_i\ (|D_i|=n_i)\)

Goal：Fisher LDA目标函数：

\[\max\limits_{\mathbf{w}}J(\mathbf{w})=\frac{(m_1-m_2)^2}{s_1^2+s_2^2} \]

注意：\(J(\mathbf{w})=J(w_1,w_2,\cdots,w_d)\)

\[\begin{aligned} \left(m_{1}-m_{2}\right)^{2} &=\left(\mathbf{w}^{T}\left(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2}\right)\right)^{2} \\ &=\mathbf{w}^{T}\left(\left(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2}\right)\left(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2}\right)^{T}\right) \mathbf{w} \\ &=\mathbf{w}^{T} \mathbf{B} \mathbf{w} \end{aligned} \]

\(\mathbf{B}\) 被称为类间扩散矩阵

\[\begin{aligned} s_{1}^{2} &=\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left(a_{i}-m_{1}\right)^{2} \\ &=\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left(\mathbf{w}^{T} \mathbf{x}_{i}-\mathbf{w}^{T} \boldsymbol{\mu}_{1}\right)^{2} \\ &=\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left(\mathbf{w}^{T}\left(\mathbf{x}_{i}-\boldsymbol{\mu}_{1}\right)\right)^{2} \\ &=\mathbf{w}^{T}\left(\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left(\mathbf{x}_{i}-\boldsymbol{\mu}_{1}\right)\left(\mathbf{x}_{i}-\boldsymbol{\mu}_{1}\right)^{T}\right) \mathbf{w} \\ &=\mathbf{w}^{T} \mathbf{S}_{1} \mathbf{w} \end{aligned} \]

\(\mathbf{S}_{1}\) 被称为 \(\mathbf{D}_1\) 的扩散矩阵 \(\mathbf{S}_{1}=n_1\Sigma_1\)

类似地，\(s_{2}^{2}=\mathbf{w}^{T} \mathbf{S}_{2} \mathbf{w}\)

令 \(\mathbf{S}=\mathbf{S}_{1}+\mathbf{S}_{2}\)，则

\[\max\limits_{\mathbf{w}}J(\mathbf{w})=\frac{(m_1-m_2)^2}{s_1^2+s_2^2}=\frac{\mathbf{w}^{T} \mathbf{B} \mathbf{w}}{\mathbf{w}^{T} \mathbf{S} \mathbf{w}} \]

注意：

\[\frac{d}{d\mathbf{w}}J(\mathbf{w})=\frac{2\mathbf{B}\mathbf{w}(\mathbf{w}^T\mathbf{S}\mathbf{w})-2\mathbf{S}\mathbf{w}(\mathbf{w}^T\mathbf{B}\mathbf{w})}{(\mathbf{w}^T\mathbf{S}\mathbf{w})^2}=\mathbf{0} \]

即有：

\[\begin{aligned} \mathbf{B}\mathbf{w}(\mathbf{w}^T\mathbf{S}\mathbf{w})&=\mathbf{S}\mathbf{w}(\mathbf{w}^T\mathbf{B}\mathbf{w})\\ \mathbf{B}\mathbf{w}&=\mathbf{S}\mathbf{w}\cdot\frac{\mathbf{w}^{T} \mathbf{B} \mathbf{w}}{\mathbf{w}^{T} \mathbf{S} \mathbf{w}}\\ \mathbf{B}\mathbf{w}&=J(\mathbf{w})\cdot\mathbf{S} \mathbf{w}\quad (*) \end{aligned} \]

若 \(\mathbf{S}^{-1}\) 存在，则

\[\mathbf{S}^{-1}\mathbf{B}\mathbf{w}=J(\mathbf{w})\cdot\mathbf{w} \]

故要求最大 \(J(\mathbf{w})\) ，只需 \(\mathbf{S}^{-1}\mathbf{B}\) 的最大特征值，\(\mathbf{w}\) 为其特征向量。

☆ 不求特征向量求出 \(\mathbf{w}\) 的方法

将 \(\mathbf{B}=(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})^{T}\) 代入 \((*)\) 得

\[\begin{aligned} (\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})^{T}\mathbf{w} &=J(\mathbf{w})\cdot\mathbf{S} \mathbf{w}\\ \mathbf{S}^{-1}(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})[\frac{(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})^{T}\mathbf{w}}{J(\mathbf{w})}]&=\mathbf{w} \end{aligned} \]

故只需计算 \(\mathbf{S}^{-1}(\boldsymbol{\mu}_{1}-\boldsymbol{\mu}_{2})\)，再单位化。

20.2 Kernel LDA：

事实1：如果 \(\left(\mathbf{S}_{\phi}^{-1} \mathbf{B}_{\phi}\right) \mathbf{w}=\lambda \mathbf{w}\)，那么 \(\mathbf{w}=\sum\limits_{j=1}^na_j\phi(\mathbf{x}_j)\)，证明见讲稿最后两页。

令 \(\mathbf{a}=(a_1,\cdots,a_n)^T\) 是“事实1”中的向量。

下面将 \(\max\limits_{\mathbf{w}}J(\mathbf{w})=\frac{(m_1-m_2)^2}{s_1^2+s_2^2}=\frac{\mathbf{w}^{T} \mathbf{B}_{\phi} \mathbf{w}}{\mathbf{w}^{T} \mathbf{S}_{\phi} \mathbf{w}}\) 的问题转化为 \(\max G(\mathbf{a})\) s.t. 使用 \(\mathbf{K}\) 能求解。

注意到：

\[\begin{aligned} m_{i}=\mathbf{w}^{T} \boldsymbol{\mu}_{i}^{\phi} &=\left(\sum_{j=1}^{n} a_{j} \phi\left(\mathbf{x}_{j}\right)\right)^{T}\left(\frac{1}{n_{i}} \sum_{\mathbf{x}_{i} \in \mathbf{D}_{i}} \phi\left(\mathbf{x}_{k}\right)\right) \\ &=\frac{1}{n_{i}} \sum_{j=1}^{n} \sum_{\mathbf{x}_{k} \in \mathbf{D}_{i}} a_{j} \phi\left(\mathbf{x}_{j}\right)^{T} \phi\left(\mathbf{x}_{k}\right) \\ &=\frac{1}{n_{i}} \sum_{j=1}^{n} \sum_{\mathbf{x}_{k} \in \mathbf{D}_{i}} a_{j} K\left(\mathbf{x}_{j}, \mathbf{x}_{k}\right) \\ &=\mathbf{a}^{T} \mathbf{m}_{i} \end{aligned} \]

其中，

\[\mathbf{m}_{i}=\frac{1}{n_{i}}\left(\begin{array}{c} \sum\limits_{\mathbf{x}_{k} \in \mathbf{D}_{i}} K\left(\mathbf{x}_{1}, \mathbf{x}_{k}\right) \\ \sum\limits_{\mathbf{x}_{k} \in \mathbf{D}_{i}} K\left(\mathbf{x}_{2}, \mathbf{x}_{k}\right) \\ \vdots \\ \sum\limits_{\mathbf{x}_{k} \in \mathbf{D}_{i}} K\left(\mathbf{x}_{n}, \mathbf{x}_{k}\right) \end{array}\right)_{n\times 1} \]

故

\[\begin{aligned} \left(m_{1}-m_{2}\right)^{2} &=\left(\mathbf{w}^{T} \boldsymbol{\mu}_{1}^{\phi}-\mathbf{w}^{T} \boldsymbol{\mu}_{2}^{\phi}\right)^{2} \\ &=\left(\mathbf{a}^{T} \mathbf{m}_{1}-\mathbf{a}^{T} \mathbf{m}_{2}\right)^{2} \\ &=\mathbf{a}^{T}\left(\mathbf{m}_{1}-\mathbf{m}_{2}\right)\left(\mathbf{m}_{1}-\mathbf{m}_{2}\right)^{T} \mathbf{a} \\ &=\mathbf{a}^{T} \mathbf{M a} \end{aligned} \]

（\(\mathbf{M}\) 被称为核类间扩散矩阵）

\[\begin{aligned} s_{1}^{2} &=\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left\|\mathbf{w}^{T} \phi\left(\mathbf{x}_{i}\right)-\mathbf{w}^{T} \boldsymbol{\mu}_{1}^{\phi}\right\|^{2} \\ &=\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left\|\mathbf{w}^{T} \phi\left(\mathbf{x}_{i}\right)\right\|^{2}-2 \sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}} \mathbf{w}^{T} \phi\left(\mathbf{x}_{i}\right) \cdot \mathbf{w}^{T} \boldsymbol{\mu}_{1}^{\phi}+\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left\|\mathbf{w}^{T} \boldsymbol{\mu}_{1}^{\phi}\right\|^{2} \\ &=\left(\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}}\left\|\sum_{j=1}^{n} a_{j} \phi\left(\mathbf{x}_{j}\right)^{T} \phi\left(\mathbf{x}_{i}\right)\right\|^{2}\right)-2 \cdot n_{1} \cdot\left\|\mathbf{w}^{T} \boldsymbol{\mu}_{1}^{\phi}\right\|^{2}+n_{1} \cdot\left\|\mathbf{w}^{T} \boldsymbol{\mu}_{1}^{\phi}\right\|^{2}\\ &=\left(\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}} \mathbf{a}^{T} \mathbf{K}_{i} \mathbf{K}_{i}^{T} \mathbf{a}\right)-n_{1} \cdot \mathbf{a}^{T} \mathbf{m}_{1} \mathbf{m}_{1}^{T} \mathbf{a}\\ &=\mathbf{a}^{T}\left(\left(\sum_{\mathbf{x}_{i} \in \mathbf{D}_{1}} \mathbf{K}_{i} \mathbf{K}_{i}^{T}\right)-n_{1} \mathbf{m}_{1} \mathbf{m}_{1}^{T}\right) \mathbf{a} \\ &=\mathbf{a}^{T} \mathbf{N}_{1} \mathbf{a} \end{aligned} \]

类似地，令 \(\mathbf{N}_2=\left(\sum\limits_{\mathbf{x}_{i} \in \mathbf{D}_{2}} \mathbf{K}_{i} \mathbf{K}_{i}^{T}-n_{2} \mathbf{m}_{2} \mathbf{m}_{2}^{T}\right)\)

则 \(s_1^2+s_2^2=\mathbf{a}^{T} (\mathbf{N}_{1}+\mathbf{N}_{2}) \mathbf{a}=\mathbf{a}^{T}\mathbf{N} \mathbf{a}\)

故：\(J(\mathbf{w})=\frac{\mathbf{a}^{T}\mathbf{M} \mathbf{a}}{\mathbf{a}^{T}\mathbf{N} \mathbf{a}}:=G(\mathbf{a})\)

类似 20.1，\(\mathbf{M} \mathbf{a}=\lambda\mathbf{N} \mathbf{a}\)

• 若 \(\mathbf{N} ^{-1}\) 存在，\(\mathbf{N}^{-1} \mathbf{M} \mathbf{a}=\lambda \mathbf{a}\)，\(\lambda\) 取 \(\mathbf{N}^{-1} \mathbf{M}\) 的最大特征值，\(\mathbf{a}\) 是相应的特征向量。

• 若 \(\mathbf{N} ^{-1}\) 不存在，MATLAB 求广义逆

最后考查 \(\mathbf{w}^T\mathbf{w}=1\)，即

\[\begin{aligned} (\sum\limits_{j=1}^na_j\phi(\mathbf{x}_j))^T(\sum\limits_{i=1}^na_i\phi(\mathbf{x}_i))&=1\\ \sum\limits_{j=1}^n\sum\limits_{i=1}^na_ja_i\phi(\mathbf{x}_j)^T\phi(\mathbf{x}_i)&=1\\ \sum\limits_{j=1}^n\sum\limits_{i=1}^na_ja_iK(\mathbf{x}_i,\mathbf{x}_j)&=1\\ \mathbf{a}^T\mathbf{K}\mathbf{a}&=1 \end{aligned} \]

求出 \(\mathbf{N}^{-1} \mathbf{M}\) 的特征向量 \(\mathbf{a}\) 后，\(\mathbf{a}\leftarrow \frac{\mathbf{a}}{\sqrt{\mathbf{a}^T\mathbf{K}\mathbf{a}}}\) 以保证 \(\mathbf{w}^T\mathbf{w}=1\)

Chapter 21: Support Vector Machines (SVM)

21.1 支撑向量与余量

Set up：\(\mathbf{D}=\{(\mathbf{x}_i,y_i) \}_{i=1}^n,\mathbf{x}_i \in \mathbb{R}^d,y_i \in \{-1,1 \}\)，仅两类数据。

• 超平面 (hyperplanes，\(d-1\) 维)：\(h(\mathbf{x}):=\mathbf{w}^T\mathbf{x}+b=w_1x_1+ \cdots +w_dx_d+b\)

  其中，\(\mathbf{w}\) 是法向量，\(-{b\over w_i}\) 是 \(x_i\) 轴上的截距。

• \(\mathbf{D}\) 称为是线性可分的，如果存在 \(h(\mathbf{x})\) 使得对所有 \(y_i=1\) 的点 \(\mathbf{x}_i\) 有 \(h(\mathbf{x}_i)>0\) ，且对所有 \(y_i=-1\) 的点 \(\mathbf{x}_i\) 有 \(h(\mathbf{x}_i)<0\) ，并将此 \(h(\mathbf{x})\) 称为分离超平面。

  Remark：对于线性可分的 \(\mathbf{D}\) ，分离超平面有无穷多个。

• 点到超平面的距离：

  \[\mathbf{x}=\mathbf{x}_p+\mathbf{x}_r=\mathbf{x}_p+r\cdot\frac{\mathbf{w}}{||\mathbf{w}||}\\ \begin{aligned} h(\mathbf{x}) &=h\left(\mathbf{x}_{p}+r \frac{\mathbf{w}}{\|\mathbf{w}\|}\right) \\ &=\mathbf{w}^{T}\left(\mathbf{x}_{p}+r \frac{\mathbf{w}}{\|\mathbf{w}\|}\right)+b \\ &=\underbrace{\mathbf{w}^{T}\mathbf{x}_{p}+b}_{h\left(\mathbf{x}_{p}\right)}+r \frac{\mathbf{w}^{T} \mathbf{w}}{\|\mathbf{w}\|}\\ &=\underbrace{h\left(\mathbf{x}_{p}\right)}_{0}+r\|\mathbf{w}\| \\ &=r\|\mathbf{w}\| \end{aligned} \]

  \(\therefore r=\frac{h(\mathbf{x})}{\|\mathbf{w}\|},|r|=\frac{|h(\mathbf{x}|)}{\|\mathbf{w}\|}\)

故 \(\forall \mathbf{x}_i \in \mathbf{D}\) 到 \(h(\mathbf{x})\) 的距离是 \(y_i\frac{h(\mathbf{x}_i)}{\|\mathbf{w}\|}\)

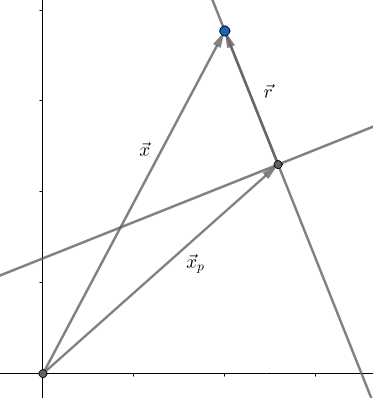
• 给定线性可分的 \(\mathbf{D}\) ，及分离超平面 \(h(\mathbf{x})\) ，定义余量：

  \[\delta^*=\min\limits_{\mathbf{x}_i}\{\frac{y_i(\mathbf{w}^T\mathbf{x}_i+b)}{\|\mathbf{w}\|} \} \]

  即 \(\mathbf{D}\) 中点到 \(h(\mathbf{x})\) 距离的最小值，使得该 \(\delta^*\) 取到的数据点 \(\mathbf{x}_i\) 被称为支撑向量（可能不唯一）。

• 标准超平面：对 \(\forall h(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b\)，以及任意 \(s\in \mathbb{R}\setminus \{0\}\)，\(s(\mathbf{w}^T\mathbf{x}+b)=0\) 与 \(h(\mathbf{x})=0\) 是同一超平面。

  设 \(\mathbf{x}^*\) 是支撑向量，若 \(sy^*(\mathbf{w}^T\mathbf{x}^*+b)=1\ (1)\) ，则称 \(sh(\mathbf{x})=0\) 是标准超平面。

  由 \((1)\) 可得：\(s=\frac{1}{y^*(\mathbf{w}^T\mathbf{x}^*+b)}=\frac{1}{y^*h(\mathbf{x}^*)}\)

  此时，对于 \(sh(\mathbf{x})=0\) ，余量 \(\delta^*=\frac{y^*h(\mathbf{x}^*)}{\|\mathbf{w}\|}=\frac{1}{\|\mathbf{w}\|}\)

事实：如果 \(\mathbf{w}^T\mathbf{x}+b=0\) 是标准超平面，对 \(\forall \mathbf{x}_i\) ，一定有 \(y_i(\mathbf{w}^T\mathbf{x}_i+b)\ge1\)

21.2 SVM: 线性可分情形

目标：寻找标准分离超平面使得其余量最大，即 \(h^*=\arg\max\limits_{\mathbf{w},b}\{\frac{1}{\mathbf{w}} \}\)

转为优化问题：

\[\begin{aligned} &\min\limits_{\mathbf{w},b}\ \{\frac{\|\mathbf{w}\|^2}{2} \}\\ &\text{s.t.} \ y_i(\mathbf{w}^T\mathbf{x}_i+b)\ge1,\forall(\mathbf{x}_i,y_i)\in \mathbf{D} \end{aligned} \]

引入 Lagrange 乘子 \(\alpha_i\ge0\) 与 KKT 条件：

\[\alpha_i(y_i(\mathbf{w}^T\mathbf{x}_i+b)-1)=0 \]

定义：

\[L(\mathbf{w})=\frac{1}{2}\|\mathbf{w}\|^2-\sum\limits_{i=1}^{n}\alpha_i(y_i(\mathbf{w}^T\mathbf{x}_i+b)-1)\ (2) \]

\[\begin{array}{l} \frac{\partial}{\partial \mathbf{w}} L=\mathbf{w}-\sum\limits_{i=1}^{n} \alpha_{i} y_{i} \mathbf{x}_{i}=\mathbf{0}\ (3) \\ \frac{\partial}{\partial b} L=\sum\limits_{i=1}^{n} \alpha_{i} y_{i}=0\ (4) \end{array} \]

将 (3)(4) 代入 (2) 得：

\[\begin{aligned} L_{d u a l} &=\frac{1}{2} \mathbf{w}^{T} \mathbf{w}-\mathbf{w}^{T}(\underbrace{\sum_{i=1}^{n} \alpha_{i} y_{i} \mathbf{x}_{i}}_{\mathbf{w}})-b\underbrace{ \sum_{i=1}^{n} \alpha_{i} y_{i}}_{0}+\sum_{i=1}^{n} \alpha_{i}\\ &=-\frac{1}{2} \mathbf{w}^{T} \mathbf{w}+\sum_{i=1}^{n} \alpha_{i}\\ &=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} \mathbf{x}_{i}^{T} \mathbf{x}_{j} \end{aligned} \]

故对偶问题为：

\[\begin{aligned} &\max\limits_{\alpha} L_{dual}=\sum_{i=1}^{n} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j} \mathbf{x}_{i}^{T} \mathbf{x}_{j}\\ &\text{s.t.}\ \sum\limits_{i=1}^{n} \alpha_{i} y_{i}=0,\alpha_i \ge0, \forall i \end{aligned} \]

利用二次规划解出 Dual：\(\alpha_1,\cdots,\alpha_n\)

代入 (3) 可得：\(\mathbf{w}=\sum\limits_{i=1}^{n} \alpha_{i} y_{i} \mathbf{x}_{i}\)

使得 \(\alpha_i>0\) 的数据 \(\mathbf{x}_i\) 给出支撑向量。

对于每一个支撑向量：\(y_i(\mathbf{w}^T\mathbf{x}_i+b)-1\Rightarrow b=\frac{1}{y_i}-\mathbf{w}^T\mathbf{x}_i\)

取 \(b=\mathop{avg}_{\alpha_i>0}\{b_i\}\)