环形数组的连续子数组最大和

描述：

给定一个长度为 n 的环形整数数组，请你求出该数组的 非空 连续子数组 的最大可能和 。

环形数组 意味着数组的末端将会与开头相连呈环状。例如，对于数组 [1,3,−5,2,−4][1,3,−5,2,−4]而言，第一个数 11的前一个数是最后一个数 −4−4。

 

输入描述：

第一行输入一个正整数 n ，代表数组的长度。
第二行为 n 个整数a_i​，每个整数之间用空格隔开，代表数组的各个元素。
1≤n≤1∗10⁵
−1∗10⁴≤a_i≤1∗10⁴

输出描述：

输出一个整数，为原数组的非空子数组的最大可能和。

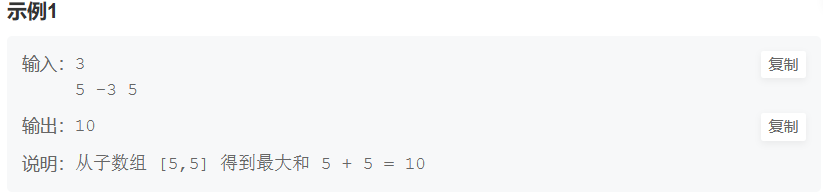
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e5+10;
int a[N];
//max_dp[i] 表示以第i个数组结尾连续值最大的
//min_dp[i] 表示以第i个数组结尾连续值最小的
//环形数组的连续子数组最大和 要么是max_dp[i]中最大的，要么是数组总和减去min_dp[i]中最小的 要想使得问题有解 只可能环形一次
int max_dp[N],min_dp[N];
int main()
{
    int n;
    cin>>n;
    int sum=0;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        sum+=a[i];
    }  
    int MAX_,MIN_;   
    MAX_=MIN_=max_dp[1]=min_dp[1]=a[1];
    for(int i=2;i<=n;i++)
    {
        max_dp[i]=max(max_dp[i-1]+a[i],a[i]);
        min_dp[i]=min(min_dp[i-1]+a[i],a[i]);
        MAX_=max(MAX_,max_dp[i]);
        MIN_=min(MIN_,min_dp[i]);
    }
    int ans=-0x3f3f3f3f;
    // cout<<MAX_<<" "<<MIN_<<" "<<endl;
    if(MIN_!=sum)
        ans=max(MAX_,sum-MIN_);
    else 
        ans=MAX_;
    cout<<ans<<endl;
}