2020.6.8训练题

A - Sum of Odd Integers

You are given two integers $n$

You have to answer $t$

$t$

The first line of the input contains one integer $t$

The next $t$

$t$

For each test case, print the answer — "YES" (without quotes) if $n$

$n$

Input

Output

YES
YES
NO
YES
YES
NO

$n$

In the first test case, you can represent $3$

In the second test case, the only way to represent $4$

In the third test case, you cannot represent $10$

In the fourth test case, you can represent $10$

In the fifth test case, you can represent $16$

In the sixth test case, you cannot represent $16$

$16$

B - Princesses and Princes

$16$

The King of Berland Polycarp LXXXIV has $n$

So Polycarp LXXXIV has enumerated his daughters from $1$

Polycarp LXXXIV is very busy, so he finds a couple for his daughters greedily one after another.

For the first daughter he takes the kingdom with the lowest number from her list and marries the daughter to their prince. For the second daughter he takes the kingdom with the lowest number from her list, prince of which hasn't been taken already. If there are no free princes in the list then the daughter marries nobody and Polycarp LXXXIV proceeds to the next daughter. The process ends after the $n$

For example, let there be $4$

In that case daughter $1$

Actually, before starting the marriage process Polycarp LXXXIV has the time to convince one of his daughters that some prince is also worth marrying to. Effectively, that means that he can add exactly one kingdom to exactly one of his daughter's list. Note that this kingdom should not be present in the daughter's list.

Polycarp LXXXIV wants to increase the number of married couples.

Unfortunately, what he doesn't have the time for is determining what entry to add. If there is no way to increase the total number of married couples then output that the marriages are already optimal. Otherwise, find such an entry that the total number of married couples increases if Polycarp LXXXIV adds it.

If there are multiple ways to add an entry so that the total number of married couples increases then print any of them.

For your and our convenience you are asked to answer $t$

$16$

The first line contains a single integer $t$

Then $t$

The first line of each test case contains a single integer $n$

Each of the next $n$

It's guaranteed that the total number of daughters over all test cases does not exceed $10^{5}$

It's also guaranteed that the total number of kingdoms in lists over all test cases does not exceed $10^{5}$

$16$

For each test case print the answer to it.

Print "IMPROVE" in the first line if Polycarp LXXXIV can add some kingdom to some of his daughter's list so that the total number of married couples increases. The second line then should contain two integers — the index of the daughter and the index of the kingdom Polycarp LXXXIV should add to that daughter's list.

If there are multiple ways to add an entry so that the total number of married couples increases then print any of them.

Otherwise the only line should contain one word "OPTIMAL".

$16$

Input

Output

IMPROVE
4 4
IMPROVE
1 1
OPTIMAL
OPTIMAL
OPTIMAL

$16$

The first test case is depicted in the statement. Adding the fourth kingdom to the list of the fourth daughter makes her marry the prince of the fourth kingdom.

In the second test case any new entry will increase the number of marriages from $0$

In the third and the fourth test cases there is no way to add an entry.

In the fifth test case there is no way to change the marriages by adding any entry.

思路：先判断新娘是否有王子与其相配，如果没有则记录一下，最后将没有相配的王子与其相配。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll nl=1e5+5;
ll a[nl],b[nl],c[nl]={0};
int main(){
       ll t;
       cin>>t;
       while(t--){
        ll n,i;
        cin>>n;
        ll k,j,temp,m=0,z,d;
        for(i=0;i<n;i++){
            cin>>k;
            temp=1;
           for(j=0;j<k;j++){
            cin>>d;
            if(temp==1){
                if(c[d]==0){
                c[d]=1;
                temp=0;
                }
            }
           }
            if(temp==1){
                m=1;
                z=i+1;
            }
           }
           if(m==0){
            cout<<"OPTIMAL"<<endl;
           }else{
            cout<<"IMPROVE"<<endl;
            cout<<z<<" ";
           }
           for(i=1;i<=n;i++){
            if(c[i]==0){
                cout<<i<<endl;
                break;
            }
           }
           for(i=0;i<=n;i++){
            c[i]=0;
           }
        }
       }

C - EhAb AnD gCd

You are given a positive integer $x$

As a reminder, $G C D (a, b)$

It's guaranteed that the solution always exists. If there are several such pairs $(a, b)$

Input

The first line contains a single integer $t$

Each testcase consists of one line containing a single integer, $x$

Output

For each testcase, output a pair of positive integers $a$

Example

Input

2
2
14

Output

1 1
6 4ple,  $G C D (1, 1) + L C M (1, 1) = 1 + 1 = 2$

In the second testcase of the sample, $G C D (6, 4) + L C M (6, 4) = 2 + 12 = 14$

$G C D (6, 4) + L C M (6, 4) = 2 + 12 = 14$

D - CopyCopyCopyCopyCopy

Ehab has an array $a$

A sequence $a$

Input

The first line contains an integer $t$

The first line of each test case contains an integer $n$

The second line contains $n$

The sum of $n$

Output

For each testcase, output the length of the longest increasing subsequence of $a$

Example

Input

2
3
3 2 1
6
3 1 4 1 5 9

Output

3
5

Note

In the first sample, the new array is $[3, 2, 1, 3, 2, 1, 3, 2, 1]$

In the second sample, the longest increasing subsequence will be $[1, 3, 4, 5, 9]$

思路：使用map记录数组中共有多少不同的数字。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll nl=1e5+5;
map<ll,ll>m;
ll a[nl];
int main(){
   ll t;
   cin>>t;
   while(t--){
   ll n;
   cin>>n;
   ll i;
   m[0]=1;
   ll num=0;
   for(i=1;i<=n;i++){
   cin>>a[i];
   if(m.count(a[i])){
        continue;
   }else{
        m[a[i]]=1;
        num++;
   }
}
cout<<num<<endl;
   m.clear();
   }
}
E - Ehab and Path-etic MEXs

You are given a tree consisting of $n$

Every label is an integer between $0$
All the written labels are distinct.
The largest value among $M E X (u, v)$

Here, $M E X (u, v)$

Input

The first line contains the integer $n$

Each of the next $n - 1$

Output

Output $n - 1$

Examples

Input

3
1 2
1 3

Output

0
1

Input

Output

Note

The tree from the second sample:

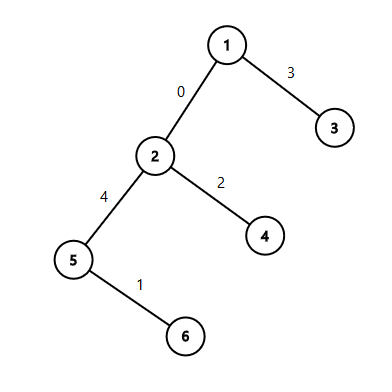
思路：先确定只有一个节点的情况，将其设为最小，其余随意。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int nl=1e5+5;
ll a[nl],b[nl],c[nl];
map<ll,ll>m;
int main(){
    ll n;
    cin>>n;
    ll i;
    for(i=1;i<=n-1;i++){
        cin>>a[i]>>b[i];
        m[a[i]]++;
        m[b[i]]++;
        c[i]=-1;
    }
    ll j=n-2;
    for(i=1;i<=n-1;i++){
        if(m[a[i]]==1||m[b[i]]==1){
            continue;
        }else{
            c[i]=j;
            j--;
        }
    }
    for(i=1;i<=n-1;i++){
        if(c[i]==-1){
            c[i]=j;
            j--;
        }
    }
    for(i=1;i<=n-1;i++){
        cout<<c[i]<<endl;
    }
}

F - Yet Another Tetris Problem

You are given some Tetris field consisting of $n$

Your task is to say if you can clear the whole field by placing such figures.

More formally, the problem can be described like this:

The following process occurs while at least one $a_{i}$

You place one figure $2 \times 1$
then, while all $a_{i}$

And your task is to determine if it is possible to clear the whole field (i.e. finish the described process), choosing the places for new figures properly.

You have to answer $t$

Input

The first line of the input contains one integer $t$

The next $2 t$

Output

For each test case, print the answer — "YES" (without quotes) if you can clear the whole Tetris field and "NO" otherwise.

Example

Input

Output

YES
NO
YES
YES

Note

The first test case of the example field is shown below:

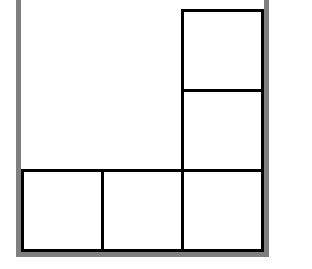
Gray lines are bounds of the Tetris field. Note that the field has no upper bound.

One of the correct answers is to first place the figure in the first column. Then after the second step of the process, the field becomes $[2, 0, 2]$

And the second test case of the example field is shown below:

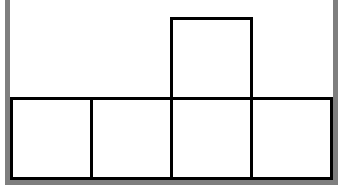
It can be shown that you cannot do anything to end the process.

In the third test case of the example, you first place the figure in the second column after the second step of the process, the field becomes $[0, 2]$

In the fourth test case of the example, place the figure in the first column, then the field becomes $[102]$

思路：本题是通过题目规定的两个条件使图形消失，因为第二条是要全部列均减一，所以要想图形一起消失，就要通过条件一使图形各列都相等。若可以则yes，否则no。注意特例，即n=1的情况。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll nl=1e5+5;
ll a[nl],b[nl];
int main(){
    ll t;
    cin>>t;
    while(t--){
        ll n;
        cin>>n;
        ll i,num=0;
        for(i=1;i<=n;i++){
            cin>>a[i];
        }
        sort(a+1,a+n);
        if(n==1){
            cout<<"YES"<<endl;
            continue;
        }
        for(i=1;i<=n-1;i++){
            b[i]=a[n]-a[i];
        }
        for(i=1;i<=n-1;i++){
            if(b[i]%2==0){
                num=1;
            }else{
                num=0;
                break;
            }
        }
        if(num==1){
            cout<<"YES"<<endl;
        }else{
            cout<<"NO"<<endl;
        }
    }
}

G - Yet Another Palindrome Problem

You are given an array $a$

Your task is to determine if $a$

Recall that an array $b$

Also, recall that a palindrome is an array that reads the same backward as forward. In other words, the array $a$

You have to answer $t$

Input

The first line of the input contains one integer $t$

Next $2 t$

It is guaranteed that the sum of $n$

Output

For each test case, print the answer — "YES" (without quotes) if $a$

Example

Input

5
3
1 2 1
5
1 2 2 3 2
3
1 1 2
4
1 2 2 1
10
1 1 2 2 3 3 4 4 5 5

Output

YES
YES
NO
YES
NO

Note

In the first test case of the example, the array $a$

In the second test case of the example, the array $a$

In the third test case of the example, the array $a$

In the fourth test case of the example, the array $a$

In the fifth test case of the example, the array $a$

$a$

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll nl=1e5+5;
ll a[nl],b[nl];
map<ll,ll>m;
int main(){
    ll t;
    cin>>t;
    while(t--){
        ll n,num=0,i;
        cin>>n;
        m[0]=1;
        for(i=1;i<=n;i++){
            cin>>a[i];
            if(m.count(a[i])){
                if(a[i-1]!=a[i]||a[i]==a[i-2]){
                    num=1;
                }
            }else{
                m[a[i]]=1;
            }
        }
        if(num==1){
            cout<<"YES"<<endl;
        }else{
            cout<<"NO"<<endl;
        }
        m.clear();
    }
}

H - Frog Jumps

There is a frog staying to the left of the string $s = s_{1} s_{2} \dots s_{n}$

Note that the frog can jump into the same cell twice and can perform as many jumps as it needs.

The frog wants to reach the $n + 1$

The frog doesn't want to jump far, so your task is to find the minimum possible value of $d$

You have to answer $t$

Input

The first line of the input contains one integer $t$

The next $t$

It is guaranteed that the sum of lengths of strings over all test cases does not exceed $2 \cdot 10^{5}$

Output

For each test case, print the answer — the minimum possible value of $d$

Example

Input

6
LRLRRLL
L
LLR
RRRR
LLLLLL
R

Output

Note

The picture describing the first test case of the example and one of the possible answers:

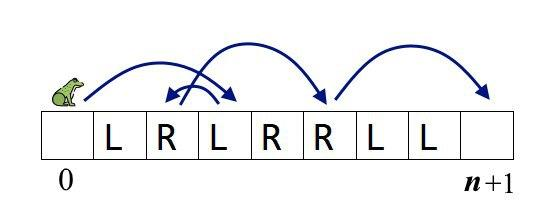
In the second test case of the example, the frog can only jump directly from $0$

In the third test case of the example, the frog can choose $d = 3$

In the fourth test case of the example, the frog can choose $d = 1$

In the fifth test case of the example, the frog can only jump directly from $0$

In the sixth test case of the example, the frog can choose $d = 1$

思路：本题要求青蛙跳一次的最短距离。可以利用数组记录R出现的位置，在用另一个数组记录R和首尾之间的距离，最后输出最大距离即可。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll nl=2e5+5;
ll b[nl],c[nl];
int main(){
    ll n;
    cin>>n;
    while(n--){
        string a;
        cin>>a;
        ll t;
        t=a.size();
        ll i,j=1;
        b[0]=0;
        for(i=0;i<t;i++){
            if(a[i]=='R'){
                b[j]=i+1;
                j++;
            }
        }
        b[j]=t+1;
        for(i=0;i<=j-1;i++){
            c[i]=b[i+1]-b[i];
        }
        sort(c,c+j);
        cout<<c[j-1]<<endl;
    }

}

posted @ 2020-06-10 10:31 yyscn 阅读(211) 评论(0) 收藏举报

刷新页面返回顶部

2020.6.8训练题

B - Princesses and Princes

C - EhAb AnD gCd

公告