OO第一单元总结

OO第一次博客作业

Task1

架构描述

​ 第一次作业我实际上采用的还是面向过程的架构设计。

​ 首先，将一个读入的多项式按照+-号分成若干项，再将项用*分开称为若干因子。而由于第一次作业的输入限制。因子只会是

a*x**b

这个形式，因此，求导就变得十分容易。而且每一个项利用*合并之后仍然满足

a*x**b

因此，我们要做的就变成了：

• 在每一项内部将因子对应相乘，化简成最简形式。
• 将这个项求导
• 将项求导后的结果相+-

因此，最终定义了5个class

Main

负责字符串的读入，正则匹配，生成项，输出

Add

项与项之间的加法运算符，代表了一个Poly加上一个Term，并将结果合并同类项。

Multi

代表了项内两个因子的相乘，满足

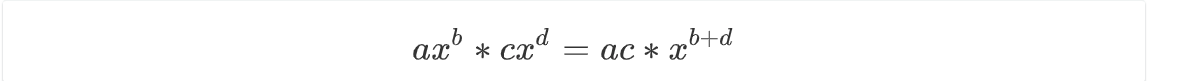
Poly

代表了一组项的相加，因此字段是一个List<Term>

定义了输出方法printPoly，可以将求导后的Poly输出。

Term

代表了一个

a*x**b

因此两个字段ceo和exp

定义了求导方法

代码分析/架构分析

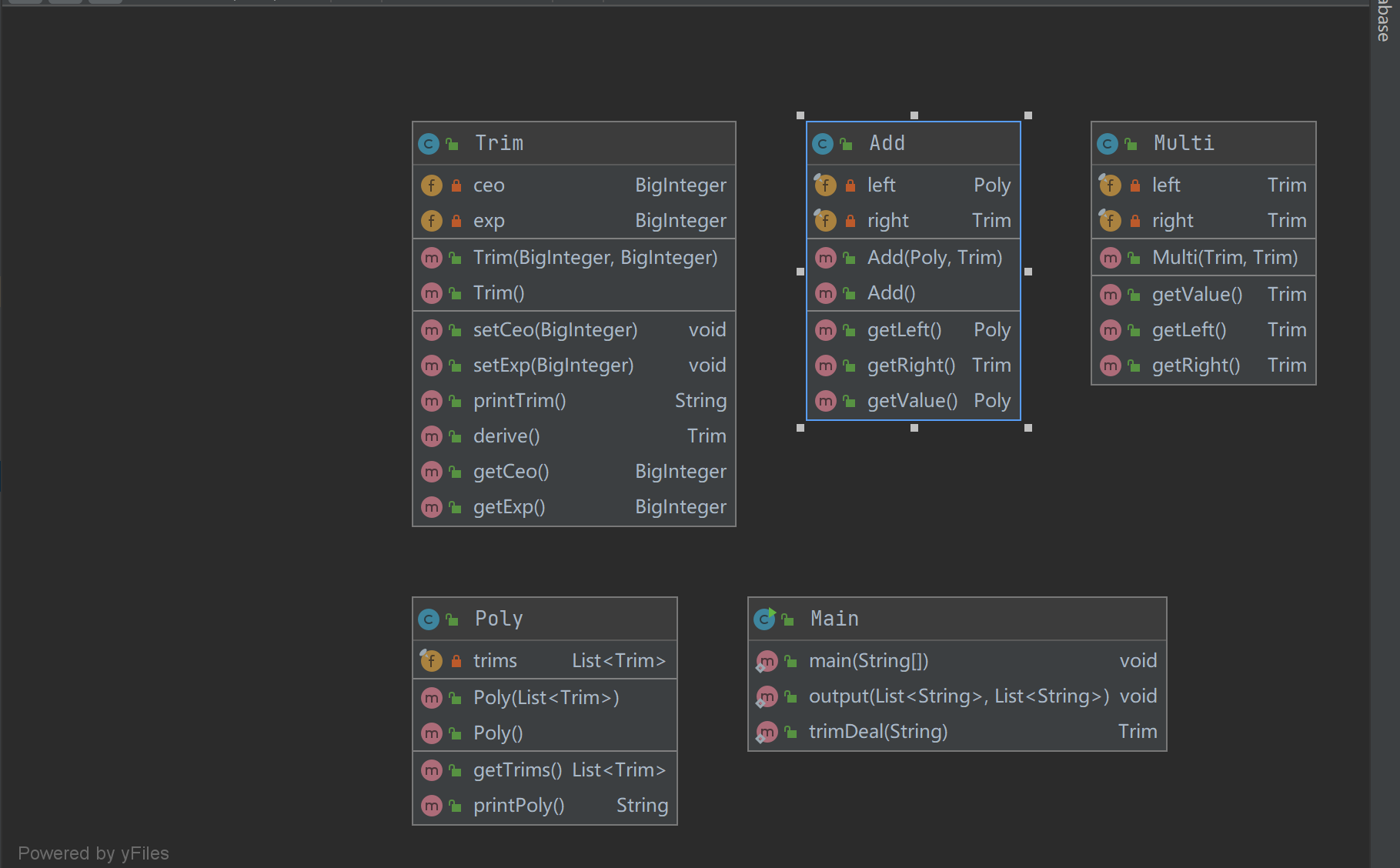
由于第一次作业输入较为固定，因此面向过程就可以很轻松的解决这个问题。这几个类之间并没有继承关系。

method	CogC	ev（G）	iv(G)	v(G)
Main.trimDeal(String)	39.0	1.0	16.0	16.0
Poly.printPoly()	26.0	7.0	11.0	12.0
Main.main(String[])	7.0	1.0	5.0	5.0
Trim.printTrim()	7.0	6.0	7.0	7.0
Add.getValue()	4.0	3.0	4.0	4.0
Main.output(List,List)	3.0	1.0	3.0	3.0
Add.Add()	0.0	1.0	1.0	1.0
Add.Add(Poly,Trim)	0.0	1.0	1.0	1.0
Add.getLeft()	0.0	1.0	1.0	1.0
Add.getRight()	0.0	1.0	1.0	1.0
Multi.Multi(Trim,Trim)	0.0	1.0	1.0	1.0
Multi.getLeft()	0.0	1.0	1.0	1.0
Multi.getRight()	0.0	1.0	1.0	1.0
Multi.getValue()	0.0	1.0	1.0	1.0
Poly.Poly()	0.0	1.0	1.0	1.0
Poly.Poly(List)	0.0	1.0	1.0	1.0
Poly.getTrims()	0.0	1.0	1.0	1.0
Trim.Trim()	0.0	1.0	1.0	1.0
Trim.Trim(BigInteger,BigInteger)	0.0	1.0	1.0	1.0
Trim.derive()	0.0	1.0	1.0	1.0
Trim.getCeo()	0.0	1.0	1.0	1.0
Trim.getExp()	0.0	1.0	1.0	1.0
Trim.setCeo(BigInteger)	0.0	1.0	1.0	1.0
Trim.setExp(BigInteger)	0.0	1.0	1.0	1.0
Total	86.0	37.0	64.0	65.0
Average	3.5833333333333335	1.5416666666666667	2.6666666666666665	2.7083333333333335

可以看到第一次作业由于架构设计基本上是面向过程的，因此基本上和c语言一个main解决问题差不多，main类中的method过于复杂，解耦性层次性差，可扩展性基本没有。

评测结果

第一次作业是没有什么bug的，强测互测均未被hack。也没有发现同房间的同学有bug。

Task2

架构描述/重构经历总结

第一次的结构只支持每一项固定为

a*x**b

的项，显然是无法满足第三次作业表达式因子嵌套的要求。

​ 因此参考第二次作业给出的提示，给出层次化的处理策略：

• 在人处理表达式的时候，我们往往不会首先关注每一个项内部的具体内容，而是忽略具体内容，在表达式层先弄清楚项的加减结构。
• 然后提取出每一项的内容分别看出分出因子，不管因子的具体内容
• 对因子进行求导
• 最后根据运算结构选择适合的组合方式，组合成为最终的导数

因此，将每一种运算符和每一种类型的因子分别建立类，考虑到运算符都至多是二元的，因此考虑使用二叉树进行组织。

类图如下：

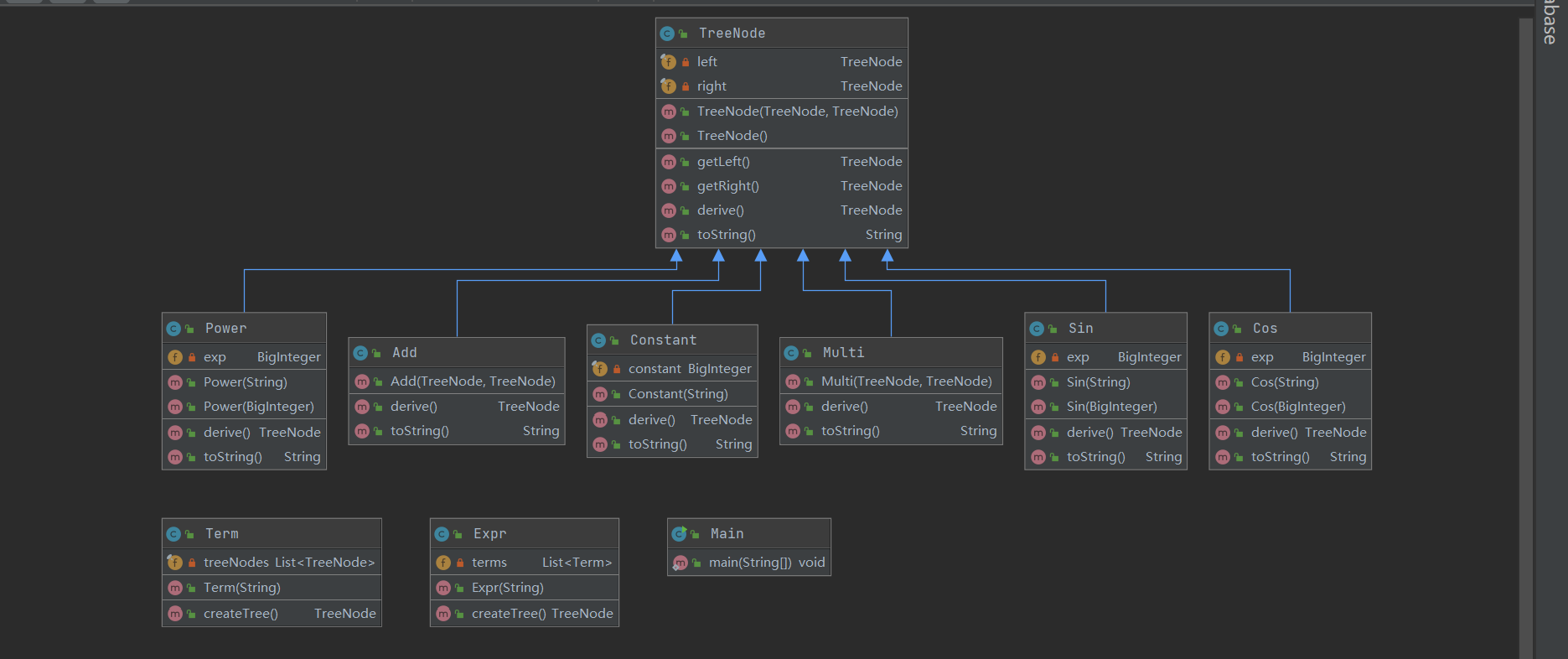
可见我定义的关系还是比较简单的，就是一次的继承。

主要还是因为这六个类有相似之处，继承自同一个TreeNode向上转型可以很好的建立树状结构，构建表达式树。

其中，TreeNode类中要定义derive和toString两个方法：

• 由于二叉树只需要根节点就可以访问全部，因此derive方法是对以本结点作为根的树进行求导的操作，返回的是一个求导后的新的树的根节点，这样方便递归调用。

• 同理：toString方法是对以本结点作为根的树进行输出的操作，返回的是一个字符串，同样可以递归调用。

而建树就采用分层处理的办法：

• 读入一个表达式串，在表达式层进行处理。不管每一项的树的具体内容，我们在表达式层只需要将每一项处理后返回的树的根节点用+连接起来成为一个新树即可。
• 在每一个项这一层，我们不关注具体的因子树是什么，而只需要在项这一层将若干因子树的根节点采用*连接起来即可。
• 而在因子层，我们用正则表达式匹配因子类型，根据因子的字符串生成对应的因子树。（表达式因子直接调用表达式的createTree方法）
• 这样分层处理，本层只接受下一层返回的子树，做到在本层将子树连接起来成为本层的结果返回到上一层继续处理即可。

下面由于不能放代码，以一个表达式来模拟整个建树求导并输出的过程：

表达式为sin(x)*cos(x)+x

建表达式树如下：

• 在表达式层：只有两项，sin(x)*cos(x)与x，分别命名为Term1和Term2，我们只需要建立一个加法类就可以。

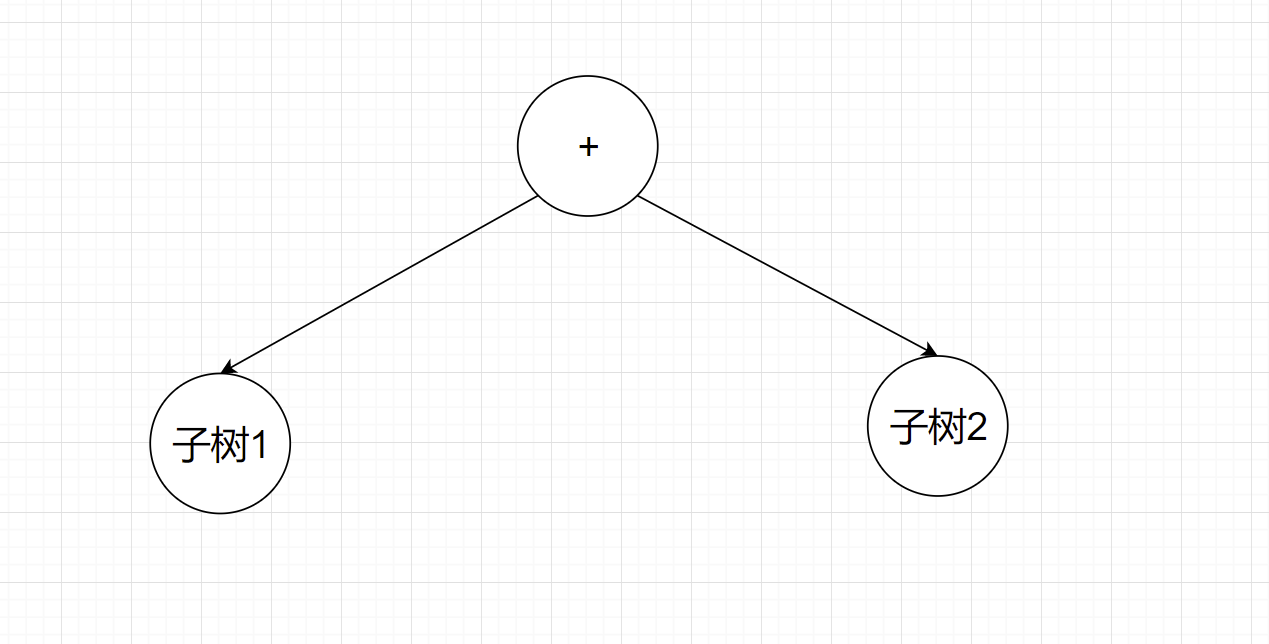
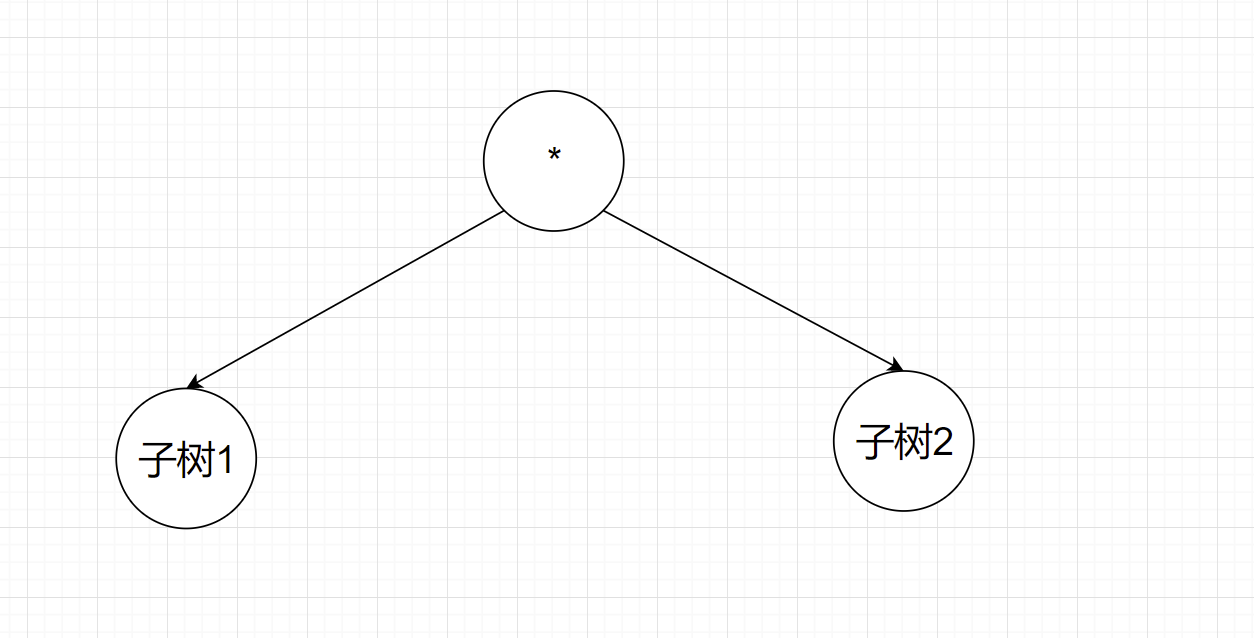
• 在项层，首先建立子树1：

  分析Term1可得，共有两个因子，为fac1=sin(x)和fac2=cos(x)

  

分析Term2可得，共有1个因子，为fac3=x,并不需要*

• 进入因子层，就可以分别建树

  树1：

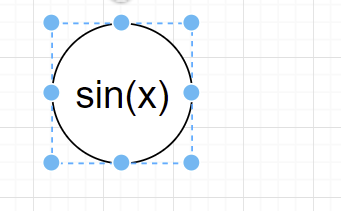
​ 树2：

​ 树3：

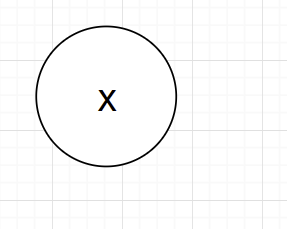
这样有了每个子树的内容，我们按照将树组装完成，建树完毕

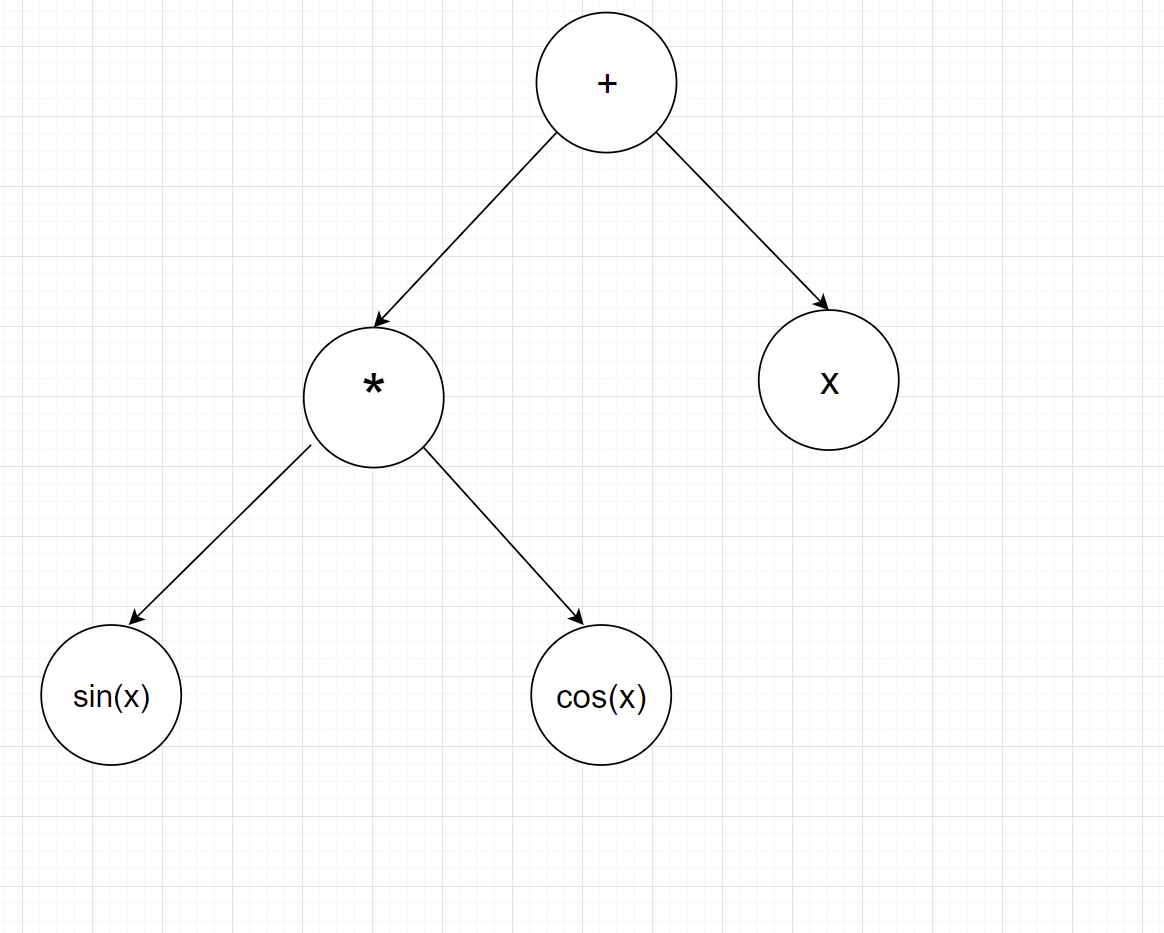
PS:这样模拟只是为了让理解分层处理的思想，代码实现直接递归调用左右子树就可以，非常方便。

对这个表达式树求导：

derive是一个对树的操作，返回的是一个求导后的新树

• 对这个表达式求导，首先调用根节点，类型是add，add求导应当是左子树求导的结果+右子树求导的结果。

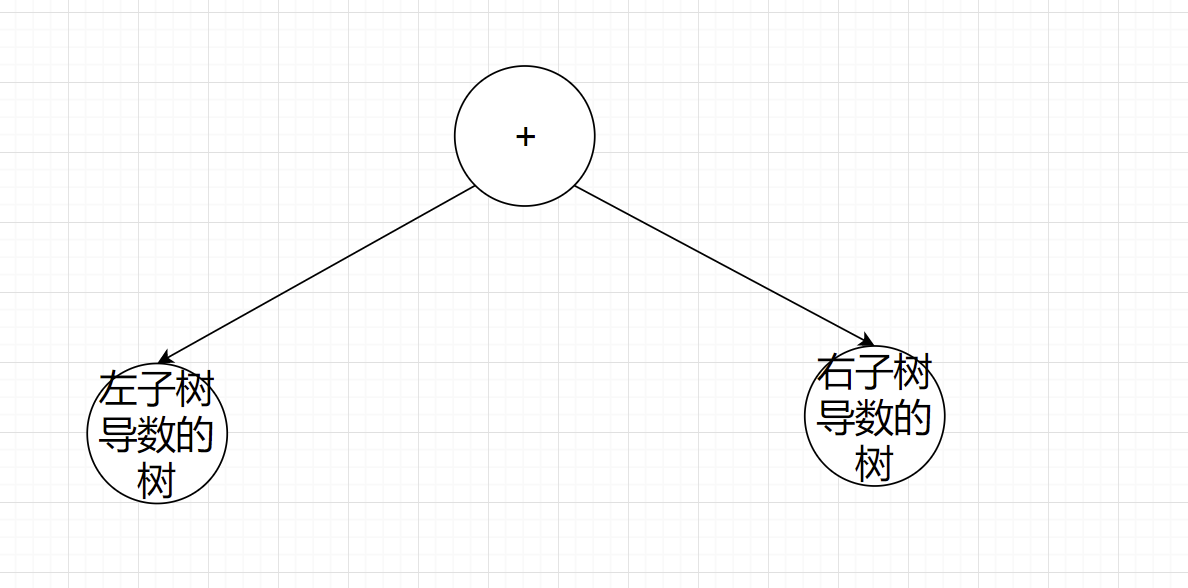
• 左子树求导，左子树根节点是一个*，而乘的求导规则是

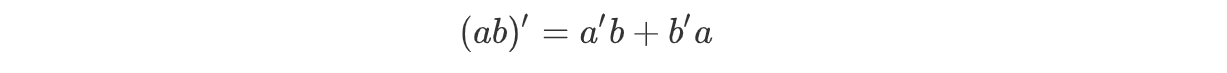
因此返回的是一个根节点为+的树

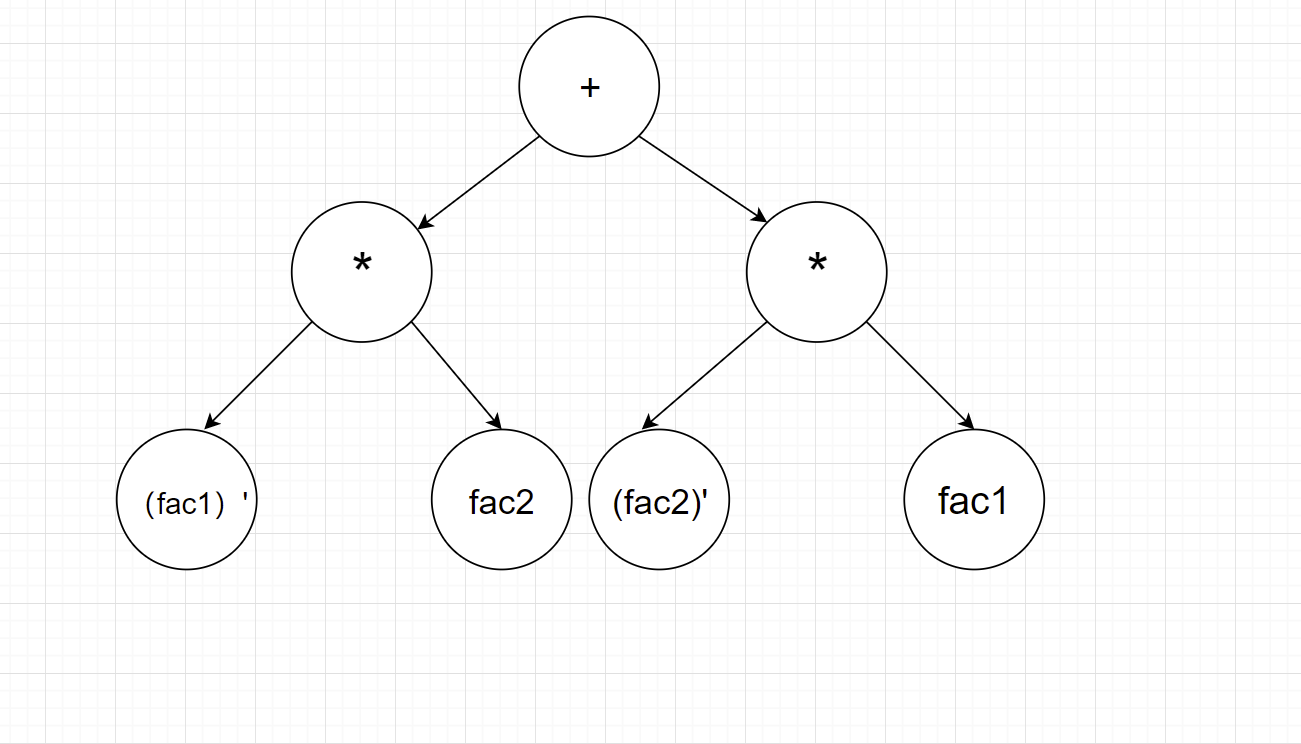
• 进入因子层，对因子求导，法则定义在这个因子类中

右子树求导同理，全部求导完毕，组装起来即可。

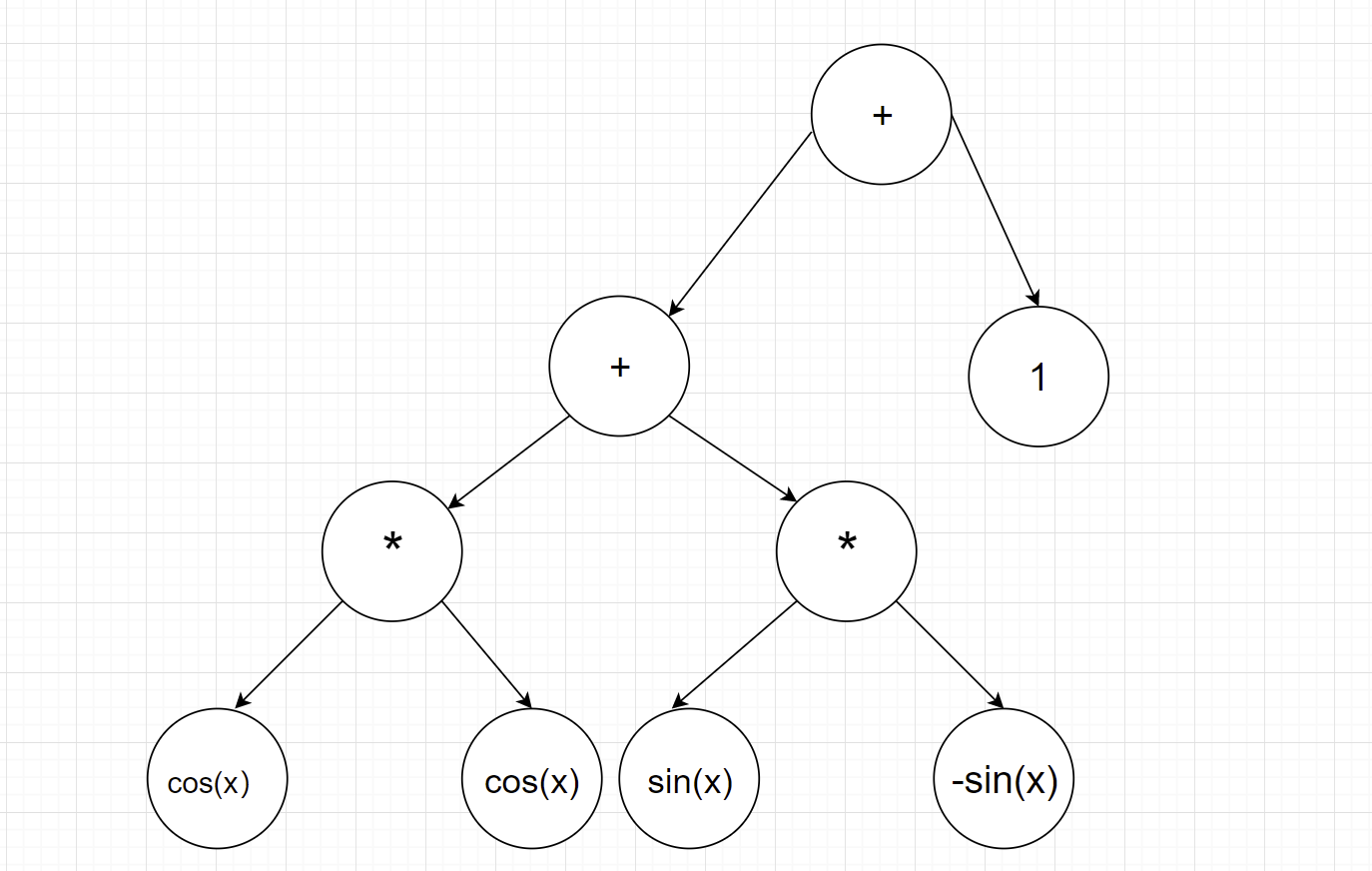
输出求导后的表达式树：

由于我们的表达式都是中缀的，每个结点都定义了toString，根据数据结构中讲过的中序遍历就可以输出了。

输出结果为

cos(x)*cos(x)+sin(x)*-1*sin(x)+1

至此，我们写的程序就已经正确了，但是优化工作仍然要做。

我的想法是，不直接改变求导后的树，毕竟直接修改树容易出事，我们只需要让这个树对应的输出内容尽量短就可以了。因此修改toString就可以了

而且toString本身就是递归调用的结果，因此我们只需要在上述定义的类中根据输出法则简化对应的toString就可以了。

比如说x**1结点的toString需要输出x这种

怕影响正确性，我只做了一些基本的优化，但强测结果就还不错。

架构分析

这样处理的关键点就在于分层，递归两个点：

• 由于表达式因子的加入，我们的每一项有非常多种形式，我们无法穷尽每一种可能。分层处理+递归的办法可以避免这些情况的考虑，我们在写高层的方法的时候可以假设底层的方法已经写好了（递归处理），只需要关注本层的内容就可以了，可以确保正确性。

• 而且这样的办法是非常符合人类的思考习惯的，试想人在做求导的时候，面对(A){+*-/}(B)的时候第一反应一定不是A式和B式的具体内容，而是先看中间的符号，确定对应的求导规则，然后再进行对应的操作。

• 这样的架构使得运算法则和因子之间的界限模糊了，毕竟都是TreeNode，这样我们可以定义更多的类来实现程序的可扩展性。

  例如：

  • 在第三次作业加入sin(因子)后，我们完全可以修改class，使得sin不再是一个单节点，而是一种运算法则，参数就是括号内的因子，这样自然而然就将sin建成了一个只有左子树fac的树根结点，cos也是同理，同样像+*一样定义对应的求导操作即可。
  • 如果后续加入了(表达式)**2这种类型的因子，我们也完全可以将Power看作一种运算法则，参数也是括号内的表达式，Power建成了一个只有左子树Expr的树根结点，同样像+*一样定义对应的求导操作即可
  • 这样的架构可扩展性就大大提升了。

测评结果

程序没有找出bug，但是由于自身的代码写法有问题，会导致TLE，希望以后注意代码细节。

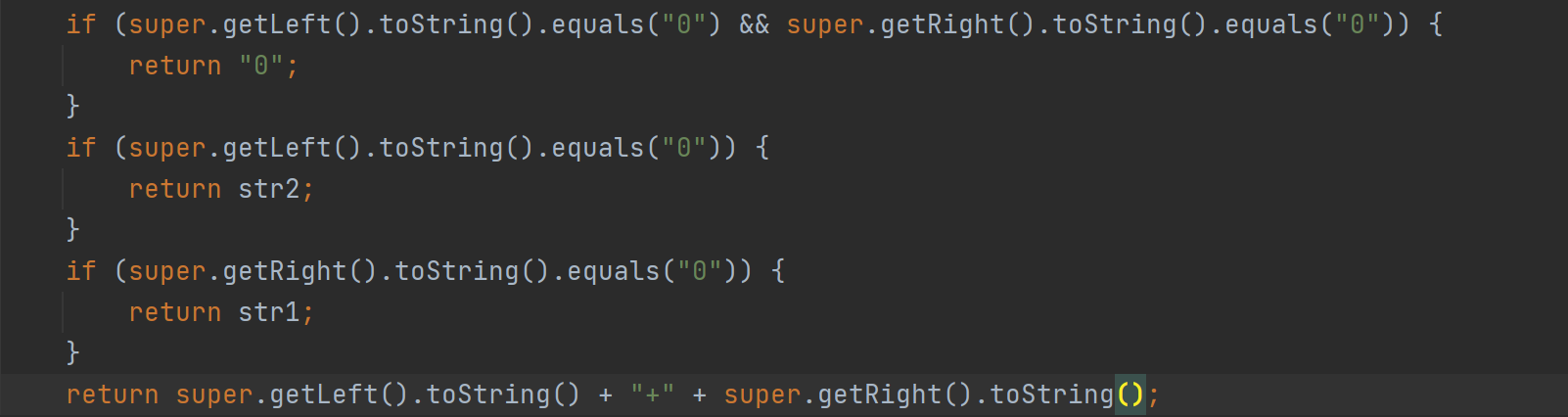
改为：

从10秒到0.2秒

测试中Hack别人都采用的是括号嵌套卡T的做法，并没有什么新意。

Task3

架构描述

task3加入sin(因子)的形式，这种处理方法上文已经讲过，不再赘述。

主要是格式检查：

​ 格式检查由于前两次作业我都是先把字符串的所有\s都删了再处理的，懒得改了，思路还是分层处理。

​ 当读入一个表达式时，在遇到像sin(fac)，（expr）这种，不管内部的fac，expr，只处理最外层的，没有括号嵌套的内容，有嵌套的即使错了，也不管，提取出括号内容后在像建树一样在下一层递归判断格式就可以了

​ 我的方法是将外层（）全部利用字符串处理换成[]，[]内部不做任何改变(一定不能改变内部的任何内容，不然忽略内部的一些错误），用正则表达式进行严格匹配（没找到能保证正确性的好方法，希望大家可以教教我）

但是正则实在太复杂了，稍有不慎就会出错

[]内部建树的时候本来就要递归调用，因此可以顺便格式检查。

比如：sin(s in(x))

现在最顶层判断处理成sin[]，符合格式

递归检查括号中的s in(x)，同样处理成s in[]，不符合格式，throw exception

代码分析

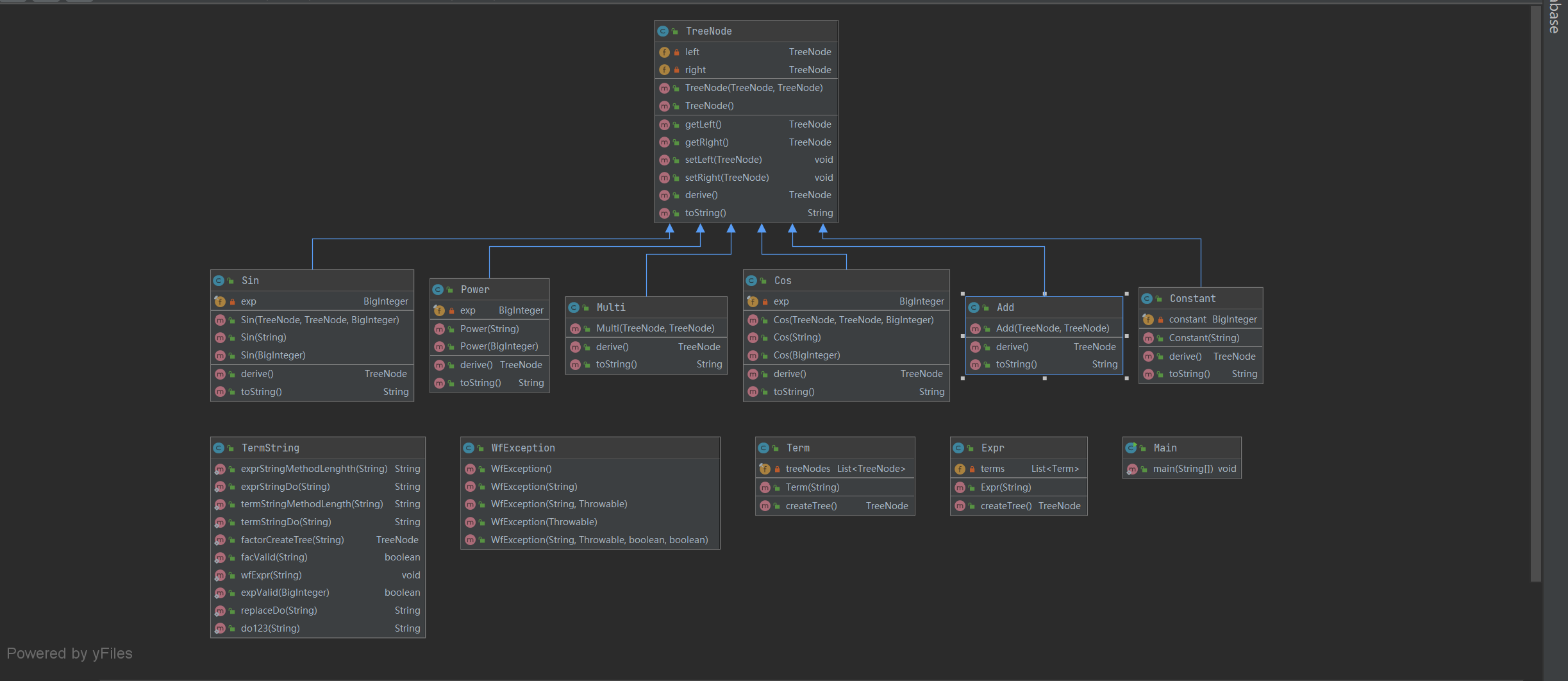
可见基本的架构和作业二没有什么改变，都是基本的因子和运算符继承自因子，但是由于Task3有复杂的格式判断，加入了一个TermString类，专门用于字符串的解析和判断是否合法，这是我认为做的比较好的地方。

method	CogC	ev（G）	iv(G)
WfException.WfException(Throwable)	0.0	1.0	1.0	1.0
WfException.WfException(String,Throwable,boolean,boolean)	0.0	1.0	1.0	1.0
WfException.WfException(String,Throwable)	0.0	1.0	1.0	1.0
WfException.WfException(String)	0.0	1.0	1.0	1.0
WfException.WfException()	0.0	1.0	1.0	1.0
TreeNode.TreeNode(TreeNode,TreeNode)	0.0	1.0	1.0	1.0
TreeNode.TreeNode()	0.0	1.0	1.0	1.0
TreeNode.toString()	0.0	1.0	1.0	1.0
TreeNode.setRight(TreeNode)	0.0	1.0	1.0	1.0
TreeNode.setLeft(TreeNode)	0.0	1.0	1.0	1.0
TreeNode.getRight()	0.0	1.0	1.0	1.0
TreeNode.getLeft()	0.0	1.0	1.0	1.0
TreeNode.derive()	0.0	1.0	1.0	1.0
TermString.wfExpr(String)	5.0	3.0	2.0	3.0
TermString.termStringMethodLength(String)	29.0	1.0	1.0	17.0
TermString.termStringDo(String)	24.0	1.0	1.0	13.0
TermString.replaceDo(String)	0.0	1.0	1.0	1.0
TermString.facValid(String)	1.0	2.0	2.0	2.0
TermString.factorCreateTree(String)	13.0	4.0	8.0	9.0
TermString.expValid(BigInteger)	1.0	2.0	1.0	2.0
TermString.exprStringMethodLenghth(String)	29.0	1.0	1.0	17.0
TermString.exprStringDo(String)	24.0	1.0	1.0	13.0
TermString.do123(String)	16.0	1.0	1.0	10.0
Term.Term(String)	15.0	3.0	10.0	10.0
Term.createTree()	4.0	2.0	2.0	4.0
Sin.toString()	7.0	5.0	3.0	5.0
Sin.Sin(TreeNode,TreeNode,BigInteger)	0.0	1.0	1.0	1.0
Sin.Sin(String)	13.0	5.0	4.0	5.0
Sin.Sin(BigInteger)	0.0	1.0	1.0	1.0
Sin.derive()	0.0	1.0	1.0	1.0
Power.toString()	2.0	3.0	1.0	3.0
Power.Power(String)	8.0	4.0	3.0	4.0
Power.Power(BigInteger)	0.0	1.0	1.0	1.0
Power.derive()	0.0	1.0	1.0	1.0
Multi.toString()	25.0	13.0	7.0	17.0
Multi.Multi(TreeNode,TreeNode)	0.0	1.0	1.0	1.0
Multi.derive()	0.0	1.0	1.0	1.0
Main.main(String[])	1.0	1.0	2.0	2.0
Expr.Expr(String)	19.0	1.0	3.0	12.0
Expr.createTree()	4.0	2.0	3.0	4.0
Cos.toString()	7.0	5.0	3.0	5.0
Cos.derive()	0.0	1.0	1.0	1.0
Cos.Cos(TreeNode,TreeNode,BigInteger)	0.0	1.0	1.0	1.0
Cos.Cos(String)	13.0	5.0	4.0	5.0
Cos.Cos(BigInteger)	0.0	1.0	1.0	1.0
Constant.toString()	0.0	1.0	1.0	1.0
Constant.derive()	0.0	1.0	1.0	1.0
Constant.Constant(String)	2.0	2.0	1.0	2.0
Add.toString()	4.0	4.0	2.0	5.0
Add.derive()	0.0	1.0	1.0	1.0
Add.Add(TreeNode,TreeNode)	0.0	1.0	1.0	1.0
Total	266.0	99.0	94.0	197.0
Average	5.215686274509804	1.9411764705882353	1.8431372549019607	3.8627450980392157

架构分析

优势：

• 这样递归检查分层处理起来比较容易，正确性比较容易得到保证
• 因为建树本来就会分层递归，因此两者可以结合一块处理，比较方便。

劣势

• 需要对表达式写正则匹配，即使忽略了括号内的内容，仍然很麻烦（正则表达式有400+个字符），对正则表达式要求很高，需要理解形式化表述，多做测试，确保正则表达式的正确性。

测评反馈

第三次作业测评出来还是除了一个bug，原因是WF判断的正则写错了，忽略了sin和cos后面紧跟着的空格，因为这个正则表达式太复杂了，当时就有点侥幸心理，没怎么测就交了，以后还是要保证充分测试。

作业总结

通过这三次作业，很好的向我展示了一个好的架构是多么的宝贵，第一次到第二次基本上是直接重构，花了很长时间。第二次到第三次几乎没有花费什么功夫。

而且这种架构下，我们可以定义任何的运算法则，或者修改任何已有的运算法则，实现程序的可扩展性。由此可见一个好的架构的重要性和OOP的优势。

但是这个单元还是有不少没有做好的地方。

• 首先是最大的问题是自己没有搭测评机。由于自身的懒惰和侥幸心理，想着自己手动构造一些测试样例就差不多了。但是在后面（尤其是WF判断上）深刻地体会到了测评机的测试点有多弱以及手动构造多么的不堪一击。而且后面的roomA大家都写得还不错，如果有测评机Hack别人将会变得简单高效，下次作业希望能打一个自动测评机。
• 然后就是输出的优化做的不够好，为了保证正确性，只是简单做了toString方法的一些特判和优化，起主要作用的还是去多层括号优化，还是有些遗憾。希望在下个单元可以本着精益求精的态度多做测试，不仅追求写对，更要追求写的漂亮。