Codeforces Round #466 (Div. 2) Solution
从这里开始
Codeforces 940A Points on the line
题目大意
定义一个可重集的距离是它中间最大的两个数之间的差,特殊地,只有一个元素的可重集的距离为0。
给定一个可重集,问最少删掉多少个数使得它的距离小于等于d。
排序后单调指针扫,或者直接开桶计数。
Code

1 /** 2 * Codeforces 3 * Problem#940A 4 * Accepted 5 * Time: 15ms 6 * Memory: 2000k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n, d; 13 int res; 14 int* ar; 15 16 inline void init() { 17 scanf("%d%d", &n, &d); 18 ar = new int[(n + 1)]; 19 for (int i = 1; i <= n; i++) 20 scanf("%d", ar + i); 21 } 22 23 inline void solve() { 24 sort (ar + 1, ar + n + 1); 25 int r = 1; 26 res = n - 1; 27 for (int i = 1; i <= n; i++) { 28 while (r < n && ar[r + 1] - ar[i] <= d) r++; 29 res = min(res, i + (n - r) - 1); 30 } 31 printf("%d", res); 32 } 33 34 int main() { 35 init(); 36 solve(); 37 return 0; 38 }
Codeforces 940B Our Tanya is Crying Out Loud
题目大意
给定一个数$n$和$k$。你有两个操作可以进行
- 将$n$减去1,花费$a$。
- 当$n$是$k$的倍数的时候,将$n$除以$k$,花费$b$。
问将$n$变为1的最小花费
当 $k = 1$ 的时候特判。
当$n$为$k$的倍数的时候,比较直接除和直接减到$\frac{n}{k}$的花费,如果前者更优就除,否则直接减到1。
当$n$不为$k$的倍数的时候,直接减到$\left \lfloor\frac{n}{k} \right \rfloor k$。
考虑如果在 $ik$ 的决策不是减到 $i$ 或者直接除 $k$ 得到 $i$,那么考虑一定是做了若干次减法操作得到 $p$ 然后再除以 $k$ 得到 $x$。不难证明先除以 $k$ 得到 $l$,再做若干次减法操作得到 $x$ 不会更劣。
Code

1 /** 2 * Codeforces 3 * Problem#940B 4 * Accepted 5 * Time: 30ms 6 * Memory: 2000k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 16 #define ll long long 17 18 ll n, k, a, b, res = 0; 19 20 inline void init() { 21 scanf(Auto""Auto""Auto""Auto, &n, &k, &a, &b); 22 } 23 24 inline void solve() { 25 if (k == 1) { 26 res = (n - 1) * a; 27 } else { 28 while (n != 1) { 29 if (n < k) { 30 res += (n - 1) * a; 31 break; 32 } else { 33 res += min((n % k) * a + b, (n - n / k) * a); 34 n /= k; 35 } 36 } 37 } 38 printf(Auto"\n", res); 39 } 40 41 int main() { 42 init(); 43 solve(); 44 return 0; 45 }
Codeforces 940C Phone Numbers
题目大意
给定一个由小写字母组成且长度为$n$的字符串$s$,要求输出一个字符串$t$,满足:
- $t$中出现的字符在$s$中也出现过
- 它的长度为$k$
- $t$的字典序大于$s$
- 在满足上述条件的所有串中,是字典序最小的一个
题目保证存在解。
当$k > n$时,直接输出字符串$s$,再补上$s$中最小的字符。
否则找到$s$中从第$k$个字符往前找第一个不是最大的字符,把它变为略比它的字符。
然后后面的补最小的字符。
Code

1 /** 2 * Codeforces 3 * Problem#940C 4 * Accepted 5 * Time: 31ms 6 * Memory: 2100k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n, k; 13 int mi = 0, ma = 25; 14 boolean exist[26]; 15 char str[100005]; 16 17 inline void init() { 18 scanf("%d%d", &n, &k); 19 memset(exist, false, sizeof(exist)); 20 scanf("%s", str + 1); 21 } 22 23 inline void solve() { 24 for (int i = 1; i <= n; i++) 25 exist[str[i] - 'a'] = true; 26 for (mi = 0; !exist[mi]; mi++); 27 for (ma = 25; !exist[ma]; ma--); 28 if (n < k) { 29 printf("%s", str + 1); 30 for (int i = n + 1; i <= k; i++) 31 putchar(mi + 'a'); 32 return; 33 } 34 int p; 35 for (p = k; p && str[p] == ma + 'a'; p--); 36 str[p]++; 37 while (!exist[str[p] - 'a']) 38 str[p]++; 39 for (p = p + 1; p <= k; p++) 40 str[p] = mi + 'a'; 41 str[k + 1] = 0; 42 puts(str + 1); 43 } 44 45 int main() { 46 init(); 47 solve(); 48 return 0; 49 }
Codeforces 940D Alena And The Heater
题目大意
给定一个数组$a$,和一个01串$b$,$b$按照如下方式生成(请自行阅读英文)
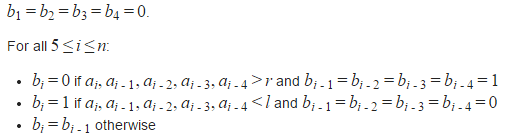
请你找出一组合法的$l, r$,保证输入存在解。
发现生成方式比较特殊。
于是根据生成方式更新$l, r$即可。
Code

1 /** 2 * Codeforces 3 * Problem#940D 4 * Accepted 5 * Time: 31ms 6 * Memory: 2500k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 11 int n; 12 int a[100005]; 13 char b[100005]; 14 15 inline void init() { 16 scanf("%d", &n); 17 for (int i = 1; i <= n; i++) 18 scanf("%d", a + i); 19 scanf("%s", b + 1); 20 } 21 22 char sameNumber(int p) { 23 char x = b[p - 1]; 24 for (int i = 2; i <= 4; i++) 25 if (b[p - i] != x) 26 return '2'; 27 return x; 28 } 29 30 int l = -1e9, r = 1e9; 31 32 inline void solve() { 33 for (int i = 5; i <= n; i++) { 34 char c = sameNumber(i); 35 if (c == '2') continue; 36 if (c == b[i]) continue; 37 if (c == '1') { 38 for (int j = 0; j <= 4; j++) 39 r = min(r, a[i - j] - 1); 40 } else { 41 for (int j = 0; j <= 4; j++) 42 l = max(l, a[i - j] + 1); 43 } 44 } 45 printf("%d %d", l, r); 46 } 47 48 int main() { 49 init(); 50 solve(); 51 return 0; 52 }
Codeforces 940E Cashback
题目大意
给定一个长度为$n$的数组和常数$c$,要求你对它进行划分。划分长度为$k$一段的代价是其中所有除去前$\left \lfloor \frac{k}{c} \right \rfloor$小的数的和。定义一个划分的代价是划分的所有段的代价的和。
问最小的代价和。
一段代价可以表示为这一段的和减去前$\left \lfloor \frac{k}{c} \right \rfloor$小的数的和。
那么考虑两段连续的长度为$c$的合并到一起,这样会使得前2小的和变小。所以划分的最长的长度不会超过$2c - 1$
那么考虑长度在$c + 1$和$2c - 1$之间的段。我只需要留一个长度为$c$的段,把它和剩下的分开。这样看的话,划分的一段的长度不会超过$c$。
继续考虑长度小于$c$的段,它的代价直接就是它中间的元素的和。因此可以直接把它分成一些只有1个元素的段。
因此存在一种最优方案满足划分的每一段长度不是1就是$c$。
因此我只用维护连续$c$个元素的最小值,以及它们的和。
于是上单调队列。
时间复杂度$O(n)$。
Code

1 /** 2 * Codeforces 3 * Problem#940E 4 * Accepted 5 * Time: 31ms 6 * Memory: 3700k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 16 #define ll long long 17 18 const int N = 100005; 19 20 int n, c; 21 int st = 1, ed = 0; 22 ll f[N]; 23 int ar[N]; 24 int que[N]; 25 26 inline void init() { 27 scanf("%d%d", &n, &c); 28 for (int i = 1; i <= n; i++) 29 scanf("%d", ar + i); 30 } 31 32 inline void solve() { 33 34 f[1] = 0; 35 ll sum = 0; 36 for (int i = 1; i <= n; i++) { 37 while (ed >= st && ar[que[ed]] >= ar[i]) ed--; 38 que[++ed] = i; 39 f[i] = f[i - 1] + ar[i]; 40 sum += ar[i]; 41 while (ed >= st && que[st] <= i - c) st++; 42 if (i >= c) 43 sum -= ar[i - c], f[i] = min(f[i], f[i - c] + sum - ar[que[st]]); 44 } 45 46 printf(Auto"\n", f[n]); 47 } 48 49 int main() { 50 init(); 51 solve(); 52 return 0; 53 }
Codeforces 940F Machine Learning
题目大意
给定一个长度为$n$的数组,要求支持两个操作:
- 询问一个区间中所有数的出现次数组成的集合的mex。
- 修改一个位置上的数。
一个可重集合的mex是这个可重集合中最小的不存在的非负整数。
这种毒瘤题?我也不会做。那就直接莫队好了。
什么?要修改?那就带修莫队好了。
唯一的问题是如何求一个集合的mex?
考虑是出现次数,所以答案不会超过500(因为$C_{500}^{2}= \frac{500 \times 499}{2}>10^{5}$),超过500次的出现次数直接扔,查询操作暴力for。
时间复杂度$O\left(n^{\frac{5}{3}}\right)$
Code

1 /** 2 * Codeforces 3 * Problem#940F 4 * Accepted 5 * Time: 1872ms 6 * Memory: 11700k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 #define pii pair<int, int> 13 #define fi first 14 #define sc second 15 16 const int cs3 = 2500, cs2 = 450; 17 18 typedef class Query { 19 public: 20 int l, r, t; 21 int id; 22 23 Query(int l = 0, int r = 0, int t = 0, int id = 0):l(l), r(r), t(t), id(id) { } 24 25 boolean operator < (Query b) const { 26 if (l / cs3 != b.l / cs3) return l < b.l; 27 if (r / cs3 != b.r / cs3) return r < b.r; 28 return t < b.t; 29 } 30 }Query; 31 32 int n, m; 33 int cm = 0, cq = 0, cd = 0; 34 int* ar; 35 Query* qs; 36 pii *ops; 37 int cnt[200005]; 38 int exist[200005]; 39 int cover[cs2]; 40 int *res; 41 map<int, int> mp; 42 43 int alloc(int x) { 44 if (mp.count(x)) return mp[x]; 45 return mp[x] = ++cd; 46 } 47 48 inline void init() { 49 scanf("%d%d", &n, &m); 50 ar = new int[(n + 1)]; 51 ops = new pii[(m + 1)]; 52 qs = new Query[(m + 1)]; 53 res = new int[(m + 1)]; 54 for (int i = 1; i <= n; i++) 55 scanf("%d", ar + i), ar[i] = alloc(ar[i]); 56 for (int i = 1, opt, l, r; i <= m; i++) { 57 scanf("%d%d%d", &opt, &l, &r); 58 if (opt == 1) 59 ++cq, qs[cq] = Query(l, r, cm, cq); 60 else 61 r = alloc(r), ops[++cm] = pii(l, r); 62 } 63 exist[0] = 211985, cover[0] = 1; 64 } 65 66 inline void update(int x, int sign) { 67 if (!exist[x] && sign == 1) cover[x / cs2]++; 68 exist[x] += sign; 69 if (!exist[x] && sign == -1)cover[x / cs2]--; 70 } 71 72 inline void updatec(int p, int sign) { 73 int x = ar[p]; 74 update(cnt[x], -1); 75 cnt[x] += sign; 76 update(cnt[x], 1); 77 } 78 79 inline void update(int op, int l, int r) { 80 int p = ops[op].fi; 81 if (l <= p && p <= r) 82 updatec(p, -1); 83 swap(ar[p], ops[op].sc); 84 if (l <= p && p <= r) 85 updatec(p, 1); 86 } 87 88 inline void solve() { 89 sort(qs + 1, qs + cq + 1); 90 int mdzzl = 1, mdzzr = 0, mdzzt = 0; 91 for (int i = 1; i <= cq; i++) { 92 while (mdzzr < qs[i].r) updatec(++mdzzr, 1); 93 while (mdzzr > qs[i].r) updatec(mdzzr--, -1); 94 while (mdzzl < qs[i].l) updatec(mdzzl++, -1); 95 while (mdzzl > qs[i].l) updatec(--mdzzl, 1); 96 while (mdzzt < qs[i].t) update(++mdzzt, mdzzl, mdzzr); 97 while (mdzzt > qs[i].t) update(mdzzt--, mdzzl, mdzzr); 98 99 for (int j = 0; j < cs2; j++) { 100 if (cover[j] < cs2) { 101 int k = j * cs2; 102 while (exist[k]) k++; 103 res[qs[i].id] = k; 104 break; 105 } 106 } 107 } 108 109 for (int i = 1; i <= cq; i++) 110 printf("%d\n", res[i]); 111 } 112 113 int main() { 114 init(); 115 solve(); 116 return 0; 117 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号