清华集训2017 Day 2简要题解
*注意:这套题目题面请在loj / uoj查看
Problem A 小 Y 和地铁
题目传送门
题目大意
小Y乘坐0号地铁线路。城市中有不超过$n + 1$条地铁线路。地铁线路不会自交,两条不同的地铁线路最多有两个交点,交点处一定是换乘站,同时也没有三条地铁线路交于一点。小Y经过了$n$个换乘站,依次给通过它们能过换到的另一条地铁线路的编号,问城市中之多还有多少个换乘站。
显然只与0号地铁相交1次的地铁线路没有用。
下面的点指的是一个换乘站,它的颜色编号指的是它能够换乘的另一条地铁的编号。
然后认真画图可以发现,连接两个颜色相同的点,实际上会将整个图划分成两个区域,所以总共有四种不同的连线方法:
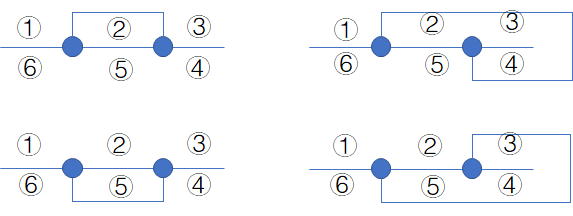
于是有了$2^{45}\times 45$的优秀做法。
我们考虑从小到达考虑每种颜色的第一个点,我们发现按照对后面的贡献可以将决策分为两种:
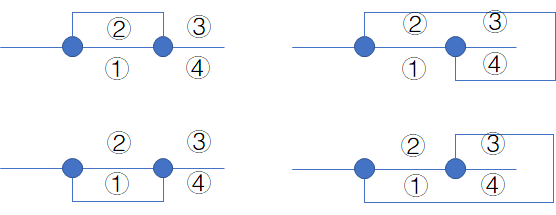
每一行的两种状态对后面的影响是一样的,所以我们可以对每一行的两种决策对当前的影响取最小值继续进行搜索。
这样时间复杂度降为$O(Tn2^{n/2})$。
加一个最优性剪枝即可通过。
Code

1 /** 2 * loj 3 * Problem#2323 4 * Accepted 5 * Time: 3349ms 6 * Memory: 252k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const int N = 50; 13 14 int T; 15 int n; 16 int ar[N], br[N], hs[N]; 17 int cup, cdn; 18 int ups[N], dns[N]; 19 20 inline void init() { 21 scanf("%d", &n); 22 memset(hs, 0, sizeof(hs)); 23 memset(ar, 0, sizeof(ar)); 24 for (int i = 1; i <= n; i++) { 25 scanf("%d", br + i); 26 ar[hs[br[i]]] = i, hs[br[i]] = i; 27 } 28 } 29 30 int res; 31 void dfs(int p, int cur) { 32 if (cur >= res) 33 return ; 34 if (p > n) { 35 res = cur; 36 return ; 37 } 38 if (!ar[p]) 39 dfs(p + 1, cur); 40 else { 41 int cnt1 = 0, cnt2 = 0; 42 for (int i = 0; i < cup; i++) { 43 cnt1 += (ups[i] > p && ups[i] < ar[p]); 44 cnt2 += (ups[i] > ar[p]); 45 } 46 for (int i = 0; i < cdn; i++) 47 cnt2 += (dns[i] > p); 48 ups[cup++] = ar[p]; 49 dfs(p + 1, cur + min(cnt1, cnt2)); 50 51 cup--, cnt1 = 0, cnt2 = 0; 52 for (int i = 0; i < cdn; i++) { 53 cnt1 += (dns[i] > p && dns[i] < ar[p]); 54 cnt2 += (dns[i] > ar[p]); 55 } 56 for (int i = 0; i < cup; i++) 57 cnt2 += (ups[i] > p); 58 dns[cdn++] = ar[p]; 59 dfs(p + 1, cur + min(cnt1, cnt2)); 60 cdn--; 61 } 62 } 63 64 inline void solve() { 65 res = 233333; 66 dfs(1, 0); 67 printf("%d\n", res); 68 } 69 70 int main() { 71 scanf("%d", &T); 72 while (T--) { 73 init(); 74 solve(); 75 } 76 return 0; 77 }
Problem B 小 Y 和二叉树
显然度数小于3的最小的点是中序遍历的第一个点,记它为$R$。(因为可以构造方案)
当主动进入一个以点$s$为根子树中时,那么第一个点一定是其中标号最小的度数小于3的点,设它的标号为$f_{s}$。
剩下的就是贪心。首先从$R$开始贪,如果它的度数为2,那么从它的左右子树中选取$f$值较小的作为右子树。
然后大概就是这样大力分类讨论。
主动进入子树和跳父亲的讨论是不一样的,所以要写两个dfs。
Code

1 /** 2 * loj 3 * Problem#2324 4 * Accepted 5 * Time: 2486ms 6 * Memory: 86200k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 typedef class IO { 13 protected: 14 const static int Limit = 65536; 15 FILE* file; 16 17 int ss, st; 18 char buf[Limit]; 19 public: 20 IO():file(NULL) { }; 21 IO(FILE* file):file(file) { } 22 23 void open(FILE *file) { 24 this->file = file; 25 } 26 27 char pick() { 28 if (ss == st) 29 st = fread(buf, 1, Limit, file), ss = 0;//, cerr << "Str: " << buf << "ED " << st << endl; 30 return buf[ss++]; 31 } 32 }IO; 33 34 #define digit(_x) ((_x) >= '0' && (_x) <= '9') 35 36 IO& operator >> (IO& in, int& u) { 37 char x; 38 while (~(x = in.pick()) && !digit(x)); 39 for (u = x - '0'; ~(x = in.pick()) && digit(x); u = u * 10 + x - '0'); 40 return in; 41 } 42 43 IO in(stdin); 44 45 const int N = 1e6 + 5; 46 const signed inf = (signed) (~0u >> 1); 47 48 int n; 49 int rt, tp = 0; 50 int f[N], deg[N]; 51 vector<int> g[N]; 52 int ans[N]; 53 54 inline void init() { 55 in >> n; 56 for (int i = 1; i <= n; i++) { 57 in >> deg[i]; 58 if (deg[i] < 3 && !rt) 59 rt = i; 60 for (int j = 0, x; j < deg[i]; j++) { 61 in >> x; 62 g[i].push_back(x); 63 } 64 } 65 } 66 67 int cnt = 0; 68 void dp(int p, int fa) { 69 cnt++; 70 f[p] = ((deg[p] < 3) ? (p) : (inf)); 71 for (int i = 0, e; i < deg[p]; i++) 72 if ((e = g[p][i]) != fa) { 73 dp(e, p); 74 f[p] = min(f[p], f[e]); 75 } 76 } 77 78 #define s1 son[0] 79 #define s2 son[1] 80 81 void dfs1(int p, int fa) { // a certain subtree 82 int son[2], top = 0; 83 for (int i = 0, e; i < deg[p]; i++) 84 if ((e = g[p][i]) != fa) 85 son[top++] = e; 86 if (!top) { 87 ans[tp++] = p; 88 } else if (top == 1) { 89 if (p < f[s1]) 90 ans[tp++] = p, dfs1(s1, p); 91 else 92 dfs1(s1, p), ans[tp++] = p; 93 } else { 94 if (f[s1] < f[s2]) 95 dfs1(s1, p), ans[tp++] = p, dfs1(s2, p); 96 else 97 dfs1(s2, p), ans[tp++] = p, dfs1(s1, p); 98 } 99 } 100 101 void dfs2(int p, int fa) { // haven't known which node is root yet 102 int son[2], top = 0; 103 for (int i = 0, e; i < deg[p]; i++) 104 if ((e = g[p][i]) != fa) 105 son[top++] = e; 106 ans[tp++] = p; 107 if (!top) 108 return; 109 if (top == 1) { 110 if (s1 <= f[s1]) 111 dfs2(s1, p); 112 else 113 dfs1(s1, p); 114 } else { 115 if (f[s1] < f[s2]) 116 dfs1(s1, p), dfs2(s2, p); 117 else 118 dfs1(s2, p), dfs2(s1, p); 119 } 120 } 121 122 inline void solve() { 123 dp(rt, 0); 124 dfs2(rt, 0); 125 for (int i = 0; i < n; i++) 126 printf("%d ", ans[i]); 127 } 128 129 int main() { 130 init(); 131 solve(); 132 return 0; 133 }
Problem C 小 Y 和恐怖的奴隶主
直接做期望不好做(就是傻逼想直接算期望,然后发现非常难去掉非法转移),我们考虑计算概率,每次转移的时候更新期望。这样就能把转移化成乘上某个矩阵。
然后发现多组询问,很GG。我们倍增一下,向量乘矩阵就行了。
这道题交uoj可能需要优化一下,某larryzhong出极限数据卡人。
我们来讲讲这道题怎么卡常:
- 矩阵不要开结构体。
- 矩阵乘法直接写代码乘,不写函数或重载运算符
- 矩阵乘法时取大小模数,小模数是题目模数,大模数是在1次乘法中不会爆掉的模数,并且必须是小模数的倍数,然后每次矩阵乘法中的乘直接乘,加变成在大模数意义下加,运算完后再将所有数对小模数取模。
- 加的时候加取模优化。
- 矩阵乘法时使用恰当的循环顺序改善内存访问。
然后就可以跑在std前面了。
Code

1 /** 2 * uoj 3 * Problem#340 4 * Accepted 5 * Time: 2267ms 6 * Memory: 14264k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 typedef bool boolean; 16 #define ll long long 17 18 const int M = 998244353; 19 const ll Mod = 3ll * M * M; 20 const int bzmax = 60; 21 22 ll Add(ll a, ll b) { 23 return ((a += b) >= Mod) ? (a - Mod) : (a); 24 } 25 26 const int N = 167; 27 28 int qpow(int a, int p) { 29 if (p < 0) 30 p += M - 1; 31 ll rt = 1, pa = a; 32 for ( ; p; p >>= 1, pa = pa * pa % M) 33 if (p & 1) 34 rt = rt * pa % M; 35 return rt; 36 } 37 38 int T; 39 ll n; 40 int m, K; 41 int cS = 0; 42 int id[9][9][9]; 43 ll v1[N], v2[N]; 44 ll *f, *bf; 45 ll powg[bzmax][N][N]; 46 47 int addServlant(int x, int y, int z) { 48 if (x + y + z == K) 49 return id[x][y][z]; 50 return id[x + (m == 1)][y + (m == 2)][z + (m == 3)]; 51 } 52 53 inline void init() { 54 scanf("%d%d%d", &T, &m, &K); 55 56 for (int i = 0; i <= K; i++) 57 for (int j = 0; i + j <= K && (m >= 2 || !j); j++) 58 for (int k = 0; i + j + k <= K && (m == 3 || !k); k++) 59 id[i][j][k] = cS++; 60 cS++; 61 62 ll (*g)[N] = powg[0]; 63 for (int i = 0; i <= K; i++) 64 for (int j = 0; i + j <= K && (m >= 2 || !j); j++) 65 for (int k = 0; i + j + k <= K && (m == 3 || !k); k++) { 66 int l = i + j + k + 1, s = id[i][j][k]; 67 ll invl = qpow(l, -1); 68 if (i) 69 g[s][id[i - 1][j][k]] = invl * i % M; 70 if (j) 71 g[s][addServlant(i + 1, j - 1, k)] = invl * j % M; 72 if (k) 73 g[s][addServlant(i, j + 1, k - 1)] = invl * k % M; 74 g[s][s] = invl, g[s][cS - 1] = invl; 75 } 76 g[cS - 1][cS - 1] = 1; 77 78 for (int i = 1; i < bzmax; i++) { 79 ll (*A)[N] = powg[i - 1], (*B)[N] = powg[i]; 80 for (int x = 0; x < cS; x++) 81 for (int k = 0; k < cS; k++) 82 for (int y = 0; y < cS; y++) 83 B[x][y] = Add(B[x][y], A[x][k] * A[k][y]); 84 for (int x = 0; x < cS; x++) 85 for (int y = 0; y < cS; y++) 86 B[x][y] %= M; 87 } 88 // powg[i] = powg[i - 1] * powg[i - 1]; 89 } 90 91 inline void solve() { 92 f = v1, bf = v2; 93 while (T--) { 94 scanf(Auto, &n); 95 memset(f, 0, sizeof(ll) * N); 96 f[id[(m == 1)][(m == 2)][(m == 3)]] = 1; 97 for (int i = 0; i < bzmax; i++) 98 if ((n >> i) & 1) { 99 memset(bf, 0, sizeof(ll) * N); 100 for (int x = 0; x < cS; x++) 101 for (int k = 0; k < cS; k++) 102 bf[k] = Add(bf[k], f[x] * powg[i][x][k]); 103 for (int x = 0; x < cS; x++) 104 bf[x] %= M; 105 swap(f, bf); 106 } 107 printf("%d\n", f[cS - 1]); 108 } 109 } 110 111 int main() { 112 init(); 113 solve(); 114 return 0; 115 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号