Loj 6036 「雅礼集训 2017 Day4」编码 - 2-sat
题目传送门
题目大意
给定$n$个串,每个串只包含 '0','1','?' ,其中 '?' 至多在每个串中出现1次,它可以被替换为 '0' 或 '1' 。问是否可能任意两个不同的串不满足一个是另一个的前缀。
2-sat的是显然的。
枚举每个通配符填0还是1,然后插入Trie树。
对于Trie的每个点在2-sat中建点。
如果其中一个点被选择,那么它祖先和所有后继的结束点都不能选。(然后逆否命题连边)
对于一个包含通配符的串,通配符替换为0以及通配符替换为1的否命题等价,同样,通配符替换为1以及通配符替换为0的否命题等价(连双向边)。
对于一个不包含通配符的串,直接它到的节点的从否命题节点连一条到它的有向边。
于是我们得到边数平方的优秀做法。
考虑前缀和优化,新建一个虚点表示Trie树上,它的祖先的命题都是假。但是这样还有点问题,还要建一个点表示Trie上,它的所有后继的命题都是假。
建图比较繁杂,见下图:
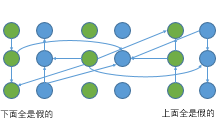
然后再说一下处理多个串在Trie树上共点。
于是便有了点数$12n$的优秀做法。再由于代码常数巨大无比,成功Loj最慢榜榜首,sad。。。(一定要去学习一下榜首同学点数$4n$的优质做法)
Code
1 /** 2 * loj.ac 3 * Problem#6036 4 * Accepted 5 * Time: 4346ms 6 * Memory: 469852k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const int N = 5e5 + 5; 13 14 typedef class TrieNode { 15 public: 16 int id; 17 TrieNode* ch[2]; 18 vector<int> vs; 19 }TrieNode; 20 21 TrieNode pool[N << 1]; 22 TrieNode* top = pool; 23 24 TrieNode* newnode() { 25 top->id = 0; 26 top->ch[0] = top->ch[1] = NULL; 27 return top++; 28 } 29 30 typedef class Trie { 31 public: 32 TrieNode* rt; 33 34 Trie():rt(newnode()) { } 35 36 int insert(char* str, int id) { 37 TrieNode* p = rt; 38 for (int i = 0, c; str[i]; i++) { 39 c = str[i] - '0'; 40 if (!p->ch[c]) 41 p->ch[c] = newnode(); 42 p = p->ch[c]; 43 } 44 if (!p->id) 45 p->id = id; 46 else if ((!p->vs.size() || p->vs[p->vs.size() - 1] != id - 1) && p->id != id - 1) 47 p->vs.push_back(id); 48 return p->id; 49 } 50 }Trie; 51 52 int n, n2; 53 char buf1[N], buf2[N]; 54 vector<int> g[N * 12]; 55 // 1 ~ 2 * n2 : Is the node seclected? 56 // 2 * n2 + 1 ~ 4 * n2: Aren't nodes above seclected? 57 // 4 * n2 + 1 ~ 6 * n2: Aren't nodes below seclected? 58 Trie tr; 59 60 inline void init() { 61 scanf("%d", &n); 62 n2 = n << 1; 63 for (int i = 1, len, p1, p2; i <= n; i++) { 64 scanf("%s", buf1); 65 len = strlen(buf1); 66 memcpy(buf2, buf1, len + 1); 67 for (int j = 0; j < len; j++) 68 if (buf1[j] == '?') 69 buf1[j] = '0'; 70 for (int j = 0; j < len; j++) 71 if (buf2[j] == '?') 72 buf2[j] = '1'; 73 p1 = tr.insert(buf1, (i << 1) - 1); 74 p2 = tr.insert(buf2, i << 1); 75 if (p1 == p2) { 76 g[(i << 1) - 1 + n2].push_back((i << 1) - 1); 77 } else { 78 p1 = ((i << 1) - 1), p2 = (i << 1); 79 g[p1].push_back(p2 + n2); 80 g[p2 + n2].push_back(p1); 81 g[p2].push_back(p1 + n2); 82 g[p1 + n2].push_back(p2); 83 } 84 } 85 } 86 87 #define virt(_x) (_x + n2) 88 #define upre(_x) (_x + n2 * 2) 89 #define upvi(_x) (_x + n2 * 3) 90 #define dore(_x) (_x + n2 * 4) 91 #define dovi(_x) (_x + n2 * 5) 92 93 void dfs(TrieNode* p, int last) { 94 if (!p) return; 95 if (p->vs.size()) { 96 vector<int> &ve = p->vs; 97 for (int i = 0; i < (signed) ve.size(); i++) { 98 TrieNode* q = newnode(); 99 q->id = ve[i]; 100 q->ch[0] = p->ch[0], q->ch[1] = p->ch[1]; 101 p->ch[1] = NULL, p->ch[0] = q; 102 } 103 ve.clear(); 104 } 105 int id = p->id; 106 if (id) { 107 g[id].push_back(upvi(id)); 108 g[id].push_back(dovi(id)); 109 g[upre(id)].push_back(virt(id)); 110 g[dore(id)].push_back(virt(id)); 111 if (last) { 112 g[id].push_back(upre(last)); 113 g[upvi(last)].push_back(virt(id)); 114 g[last].push_back(dore(id)); 115 g[dovi(id)].push_back(virt(last)); 116 117 g[upre(id)].push_back(upre(last)); 118 g[upvi(last)].push_back(upvi(id)); 119 g[dore(last)].push_back(dore(id)); 120 g[dovi(id)].push_back(dovi(last)); 121 } 122 } 123 int nid = ((id) ? (id) : (last)); 124 dfs(p->ch[0], nid); 125 dfs(p->ch[1], nid); 126 } 127 128 int dfs_clock = 0; 129 stack<int> st; 130 boolean vis[N * 12], ins[N * 12]; 131 int dfn[N * 12], low[N * 12]; 132 void tarjan(int p) { 133 vis[p] = true, ins[p] = true; 134 dfn[p] = low[p] = ++dfs_clock; 135 st.push(p); 136 for (int i = 0; i < (signed) g[p].size(); i++) { 137 int e = g[p][i]; 138 if (!vis[e]) { 139 tarjan(e); 140 low[p] = min(low[p], low[e]); 141 } else if (ins[e]) 142 low[p] = min(low[p], dfn[e]); 143 } 144 145 if (dfn[p] == low[p]) { 146 int cur; 147 do { 148 cur = st.top(); 149 st.pop(); 150 low[cur] = low[p]; 151 ins[cur] = false; 152 } while (cur != p); 153 } 154 } 155 156 void putans(const char* str) { 157 puts(str); 158 exit(0); 159 } 160 161 inline void solve() { 162 dfs(tr.rt, 0); 163 for (int i = 1; i <= n2 * 6; i++) 164 if (!vis[i]) 165 tarjan(i); 166 for (int i = 1; i <= n2; i++) { 167 if (low[i] == low[virt(i)]) 168 putans("NO"); 169 if (low[upre(i)] == low[upvi(i)]) 170 putans("NO"); 171 if (low[dore(i)] == low[dovi(i)]) 172 putans("NO"); 173 } 174 putans("YES"); 175 } 176 177 int main() { 178 init(); 179 solve(); 180 return 0; 181 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号