Codeforces Round #503 (by SIS, Div. 2) Solution
从这里开始
瞎扯
例行快速切A、B、C。
然后发现D是交互。E也不像是我能做的题,感觉完蛋了。
最后8分钟想出D。狂码代码,然后比赛结束后1分钟过样例。
第二天早上再花4分钟AC。我真是个大菜逼。。
于是这场cf比赛变成了真·手速场。几个friends手速比我快,然后rank就比我高。。。
(获得成就:在官方题解出来之前写完也许是假的题解)
Problem A New Building for SIS
题目大意
有$n$栋高度均为$h$的塔排成1排。相邻的塔之间第$a$层到第$b$层之间有通道。上下楼层或者在通道中移动均会花费1的单位时间。多次询问从一座塔的某一层到另一个塔的一层需要的最少耗时。
大力分类讨论。我居然WA了一次。'
Code

1 /** 2 * Codeforces 3 * Problem#1020A 4 * Accepted 5 * Time: 31ms 6 * Memory: 0k 7 */ 8 #include<bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n, h, a, b, q; 13 14 inline void init() { 15 scanf("%d%d%d%d%d", &n, &h, &a, &b, &q); 16 } 17 18 inline void solve() { 19 while(q--){ 20 int x1, y1, x2, y2; 21 scanf("%d%d%d%d", &x1, &y1, &x2, &y2); 22 if(y1 > y2) 23 swap(y1, y2); 24 if (x1 == x2) { 25 printf("%d\n", abs(y1 - y2)); 26 } else { 27 int ans = abs(x1 - x2); 28 if (y1 <= b && y2 >= a) { 29 ans += abs(y1 - y2); 30 }else{ 31 ans += min(abs(y1 - a) + abs(y2 - a), abs(y1 - b) + abs(y2 - b)); 32 } 33 printf("%d\n", ans); 34 } 35 } 36 } 37 38 int main(){ 39 init(); 40 solve(); 41 return 0; 42 }
Problem B Badge
题目大意
给定基环内向树。问从每个点出发,第二次到达的点是什么。
直接模拟。
Code

1 /** 2 * Codeforces 3 * Problem#1020B 4 * Accepted 5 * Time: 31ms 6 * Memory: 0k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n; 13 int *ps; 14 boolean *vis; 15 16 inline void init() { 17 scanf("%d", &n); 18 ps = new int[(n + 1)]; 19 vis = new boolean[(n + 1)]; 20 for (int i = 1; i <= n; i++) 21 scanf("%d", ps + i); 22 } 23 24 inline void solve() { 25 for (int i = 1; i <= n; i++) { 26 int j = i; 27 memset(vis, 0, sizeof(boolean) * (n + 1)); 28 while (!vis[j]) { 29 vis[j] = true; 30 j = ps[j]; 31 } 32 printf("%d ", j); 33 } 34 } 35 36 int main() { 37 init(); 38 solve(); 39 return 0; 40 }
Problem C Elections
题目大意
有$n$个人为$m$个政党投票。每个人初始投票的政党为$p_{i}$,你可以花费$v_{i}$将他投票的政党改为你指定的政党。如果使1号政党的投票严格大于其他政党,问最少花费。(这些人不正直,居然拿钱可以收买)
暴力枚举1号党最少的选票。然后贪心地收买投其他政党的人。
Code

1 /** 2 * Codeforces 3 * Problem#1020C 4 * Accepted 5 * Time: 46ms 6 * Memory: 200k 7 */ 8 #include <bits/stdc++.h> 9 #ifndef WIN32 10 #define Auto "%lld" 11 #else 12 #define Auto "%I64d" 13 #endif 14 using namespace std; 15 typedef bool boolean; 16 #define ll long long 17 18 const int N = 3005; 19 const signed ll llf = (signed ll) (~0ull >> 1); 20 21 typedef class Voter { 22 public: 23 int to; 24 int v; 25 int id; 26 27 Voter() { } 28 Voter(int to, int v, int id):to(to), v(v), id(id) { } 29 30 boolean operator < (Voter b) const { 31 return v < b.v; 32 } 33 }Voter; 34 35 int n, m; 36 ll res = llf; 37 Voter ar[N]; 38 vector<Voter> vs[N]; 39 40 inline void init() { 41 scanf("%d%d", &n, &m); 42 for (int i = 1, p, v; i <= n; i++) { 43 scanf("%d%d", &p, &v); 44 vs[p].push_back(Voter(p, v, i)); 45 ar[i] = Voter(p, v, i); 46 } 47 } 48 49 boolean sec[N]; 50 inline void solve() { 51 sort(ar + 1, ar + n + 1); 52 for (int i = 1; i <= m; i++) 53 sort(vs[i].begin(), vs[i].end()); 54 for (int p1 = vs[1].size(); p1 <= n; p1++) { 55 ll cmp = 0; 56 int got = vs[1].size(); 57 memset(sec, false, sizeof(sec)); 58 for (int i = 2; i <= m; i++) { 59 int s = vs[i].size() - p1 + 1; 60 for (int j = 0; j < s && j < vs[i].size(); j++) 61 cmp += vs[i][j].v, got++, sec[vs[i][j].id] = true; 62 } 63 int p = 1; 64 while (got < p1) { 65 if (!sec[ar[p].id] && ar[p].to > 1) { 66 cmp += ar[p].v; 67 sec[ar[p].id] = true; 68 got++; 69 } 70 p++; 71 } 72 res = min(res, cmp); 73 } 74 printf(Auto, res); 75 } 76 77 int main() { 78 init(); 79 solve(); 80 return 0; 81 }
Problem D The hat
题目大意
$2n$个数围成一圈,顺时针依次记为$a_{1}, a_{2}, \cdots, a_{2n}$,满足相邻两个数的差恰好为1。问是否存在一个$i(1\leqslant i \leqslant n)$,使得$a_{i} = a_{i + n}$。
你可以从标准输入中读取$2n$。然后你可以通过 "? x" 来询问$a_{x}$的值。最后通过 "! i" 输出你找到的$i$。如果不存在输出 "! -1" 。
你至多可以询问59次。
将每一个数和后一个数作差可以得到一个$+1, -1$构成的圈。从适当的位置剖开,等价于询问是否存在一个长度为$n$的一段和为$0$。
显然,当$n$为奇数的时候无解。因为$+1, -1$在长度为$n$的序列中必然不相等。
考虑$a_{1}$和$a_{n + 1}$。不妨先假设$a_{n + 1} - a_{1} = x\ \ (x > 0)$(如果取等直接输出答案)
如果存在解,如果它们的位置是$p_{1}, p_{2}\ (p_{1} < p_{2})$。那么$a_{p_{1}} - a_{1} = a_{p_{2}} - a_{1} = a_{p_{2}} + x - a_{n + 1}$.
移项可得:$a_{p_{1}} - a_{1} - (a_{p_{2}} - a_{n + 1}) = x$。
感觉没啥用。不过继续吧。
对于一个长度$k$,设$d = a_{k + 1} - a_{1} - (a_{k + n + 1} - a_{n + 1})$。
- 如果$d = x$,那么$k + 1$就是答案。
- 如果$d > x$,感受一下,就是$n + 1$到$n + k$的地方$+1$取多了。退回去一些就能找到答案。
现在来证明这个答案一定存在。
容易证明$d, x$一定是偶数。考虑每次将$k$减少,$d$可能的变化量有$-2, 0, 2$。
当$k = 0$的时候,$d_{0} = 0$。$d$从一个大于$x$的偶数,每次变化为$-2, 0, 2$。
显然一定存在某个时刻$d = x$。(否则任意$d' \leqslant x - 2$无法被取到,但$k = 0$时$d = 0 \leqslant x - 2$)。 - 如果$d < x$。我们考虑增加$k$,当$k = n$是$d_{n} = x - (-x) = 2x$。因为$x > 0$,同理可以证得存在某个时刻$d = x$。
根据以上讨论,发现每次指定$k$后,能确定答案至少存在于一半的区间。因此可以二分。
对于$x < 0$的情况作类似的讨论也可以得出类似的结论。
UPD 2019.9.1
觉得自己当时非常地蠢。其实这个问题很傻逼。
考虑 $g_i = a_{i + n/2} - a_{i} $。$g_{i + 1} - g_{i}$的差要么是0,要么是正负2.
可以先求出$g_1$,如果$g_1$是奇数,答案是-1。如果$g_1$是0,那么做完了。
根据初中数学只是我们知道,这个函数一定存在零点。
用$g_l g_r < 0$来判就行。这个显然可以二分。
Code

1 /** 2 * Codeforces 3 * Problem#1020D 4 * Accepted 5 * Time: 31ms 6 * Memory: 0k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n, hn; 13 14 int ask(int p) { 15 printf("? %d\n", p); 16 fflush(stdout); 17 int x; 18 scanf("%d", &x); 19 return x; 20 } 21 22 inline void init() { 23 scanf("%d", &n); 24 hn = (n >> 1); 25 } 26 27 inline void solve() { 28 if (hn & 1) { 29 puts("! -1"); 30 return; 31 } 32 int x = ask(1), y = ask(1 + hn); 33 if (x == y) { 34 puts("! 1"); 35 return; 36 } 37 int l = 1, r = hn - 1; 38 if (x < y) { 39 while (l <= r) { 40 int mid = (l + r) >> 1; 41 int a = ask(1 + mid) - x, b = ask(1 + mid + hn) - y; 42 if (a == b + (y - x)){ 43 printf("! %d", 1 + mid); 44 return; 45 } 46 if (a < b + (y - x)) 47 l = mid + 1; 48 else 49 r = mid - 1; 50 } 51 } else { 52 while (l <= r) { 53 int mid = (l + r) >> 1; 54 int a = ask(1 + mid) - x, b = ask(1 + mid + hn) - y; 55 if (a == b + (y - x)){ 56 printf("! %d", 1 + mid); 57 return; 58 } 59 if (a > b + (y - x)) 60 l = mid + 1; 61 else 62 r = mid - 1; 63 } 64 } 65 puts("! -1"); 66 } 67 68 int main() { 69 init(); 70 solve(); 71 return 0; 72 }
Problem E Sergey's problem
题目大意
给定一个有向无自环的图。要求选出一个点集满足:
- 点集中任意两点不能通过一条边直接到达。
- 不在点集中的某个点可以通过点集中的点经过至多2条边到达。
做法感觉很神的样子。
- 首先按标号从小到大枚举点,当一个点没有被标记时,将它加入集合$A$,然后删去它经过1条出边能够到达的点。
- 然后按标号从大到小枚举$A$中的点,如果它不在答案点集$V$中并且它所有入边的起点均不在$V$中,则将它加入$V$。
然后来证明一下它的正确性:
-
点集中任意两点不能通过一条边直接到达
假设结论不成立。那么存在一条边两端的两个点同时被选了。设这条边是$(u, v)$。
由第一步可知:$v < u$。否则$v$会在选$u$的时候被标记。
由第二步可知:$u$会被先选入$V$,之后$v$不会被选入$V$,矛盾。 -
不在点集中的某个点可以通过点集中的点经过至多2条边到达。
仍然假设结论不成立。那么必然存在一个点$p$,所有$v \in V$到它的最短路的长度至少为$3$。
考虑$p$的一个直接前驱$q$。所有$v \in V$到$q$的最短路的长度至少为$2$。
所以$q \in A$。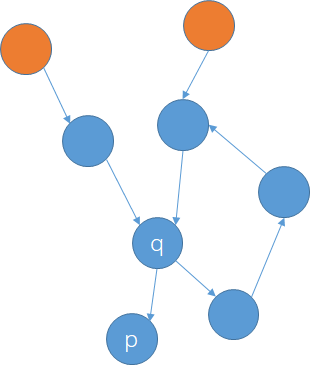
如上图橙色的点是$V$中的点(显然这个选择方案是有问题的)。然后考虑$q$在第二轮中是否能被选中。
因为$q$的直接前驱都不在$V$中,所以$q$一定能被选中。这与假设矛盾。
Code

1 /** 2 * Codeforces 3 * Problem#1020E 4 * Accepted 5 * Time: 763ms 6 * Memory: 52100k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 int n, m; 13 boolean *lab1, *lab2; 14 vector<int> *g, *rg; 15 16 inline void init() { 17 scanf("%d%d", &n, &m); 18 lab1 = new boolean[(n + 1)]; 19 lab2 = new boolean[(n + 1)]; 20 g = new vector<int>[(n + 1)]; 21 rg = new vector<int>[(n + 1)]; 22 memset(lab1, false, sizeof(boolean) * (n + 1)); 23 memset(lab2, false, sizeof(boolean) * (n + 1)); 24 for (int i = 1, u, v; i <= m; i++) { 25 scanf("%d%d", &u, &v); 26 g[u].push_back(v); 27 rg[v].push_back(u); 28 } 29 } 30 31 vector<int> curans; 32 inline void solve() { 33 for (int i = 1; i <= n; i++) { 34 if (lab1[i]) 35 continue; 36 for (int j = 0; j < (signed) g[i].size(); j++) 37 lab1[g[i][j]] = true; 38 lab1[i] = true; 39 curans.push_back(i); 40 } 41 42 for (int i = curans.size() - 1; ~i; i--) { 43 int p = curans[i]; 44 lab2[p] = true; 45 for (int j = 0; j < (signed) rg[p].size() && lab2[p]; j++) 46 if (lab2[rg[p][j]]) 47 lab2[p] = false; 48 } 49 50 curans.clear(); 51 for (int i = 1; i <= n; i++) 52 if (lab2[i]) 53 curans.push_back(i); 54 55 printf("%d\n", (signed) curans.size()); 56 for (int i = 0; i < (signed) curans.size(); i++) 57 printf("%d ", curans[i]); 58 } 59 60 int main() { 61 init(); 62 solve(); 63 return 0; 64 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号