Codeforces 932G Palindrome Partition - 回文树 - 动态规划
题目传送门
通往???的传送点
通往神秘地带的传送点
通往未知地带的传送点
题目大意
给定一个串$s$,要求将$s$划分为$t_{1}t_{2}\cdots t_{k}$,其中$2\mid k$,且$t_{i} = t_{k - i}$,问方案数。
直接做不太好做。虽然可以$O(n^{2})$进行动态规划。
考虑做一步转化:设$s' = s_{1}s_{n}s_{2}s_{n - 1}\cdots s_{n / 2}s_{n / 2 + 1}$。
然后它的一个偶回文划分可以和原来的划分一一对应。
于是可以$O(n^{2})$进行动态规划。然后完美TLE。
定理1 一个回文的后缀是回文串当且仅当它是原串的border。
根据回文串和border的定义容易证明。
引理1 (Weak Periodicity Lemma) 设$p$和$q$是$s$的周期,且$p + q \leqslant |s|$,则$(p, q)$也是$s$的周期
证明 不妨设$p < q, d = q - p$。
- 当$|s| - q\leqslant i \leqslant |s| - d$时,$s_{i} = s_{i - p} = s_{i - p + q} = s_{i + d}$
- 当$1\leqslant i < |s| - q$时,$s_{i} = s_{i + q} = s_{i + q - p} = s_{i + d}$。
然后根据辗转相除法能够得到$(p, q)$也是$s$的周期。因此定理得证。
引理2 字符串的所有长度不小于$|s| / 2$的所有border的长度构成等差数列。
证明 设$|s| - p (p\leqslant |s| / 2)$是$s$最长的$border$,另外某个border的长度是:$|s| - q (q\leqslant |s| / 2)$,那么能够推出$(p, q)$是$s$的周期,因此$|s| - (p, q)$也是字符串$s$的border。由$p$的最小性以及$(p, q)\leqslant p$可知$(p, q) = p$,即$p\mid q$。
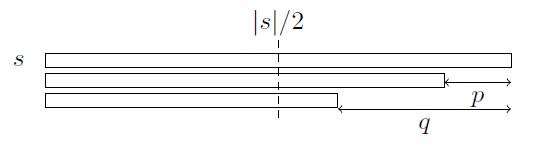
(懒得画图了,直接截论文的图)
不难证明对于任意$q (q\leqslant |s| / 2)$,且$p\mid q$的后缀是字符串$s$的border。
推论 一个字符串的border可以被分为不超过$\left \lceil log_{2}n \right \rceil$段等差数列。
证明 设$2^{k}\leqslant n < 2^{k + 1}$,考虑以下几段的border:
$\begin{matrix}[2^{k}, n]\\ [2^{k - 1}, s^{k})\\ [2^{k - 2}, 2^{k - 1})\\ \vdots \\ [1, 2)\end{matrix}$
根据引理2可得长度属于每一段的border都是一个等差数列。
因此得证。
有了这个推论有什么用呢?

对于每一类border,每一次它被成为当前前缀的border意味着当前串的长度减去周期后,这些border还被发现了一次。
如上图,每次如果能够预处理出橙色部分,转移的时候只用补上没有计算的一项就好了.
用$f[i]$表示第$i$个前缀的偶回文划分的方案数。
用$g[i]$表示在回文树的状态$i$作为等差数列末项的时候等差border的动态规划的值的和。
建回文树的时候记一下dif和slink就可知道等差数列的差以及上一类等差数列的末项。
Code
1 /** 2 * Codeforces 3 * Problem#932G 4 * Accepted 5 * Time: 93ms 6 * Memory: 128200k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const int alpha = 26; 13 14 typedef class TrieNode { 15 public: 16 int len, dif, g; 17 TrieNode *ch[alpha]; 18 TrieNode *fail, *slink; 19 }TrieNode; 20 21 typedef class PalindromeTree { 22 public: 23 int len; 24 TrieNode *pool; 25 TrieNode *top; 26 TrieNode *odd, *even; 27 TrieNode *last; 28 char *str; 29 30 TrieNode* newnode(int len) { 31 top->len = len, top->dif = -1, top->g = 0; 32 memset(top->ch, 0, sizeof(top->ch)); 33 top->fail = top->slink = NULL; 34 return top++; 35 } 36 37 PalindromeTree() { } 38 PalindromeTree(int n) { 39 pool = new TrieNode[(n + 5)]; 40 str = new char[(n + 5)]; 41 top = pool, len = 0; 42 odd = newnode(-1), even = newnode(0); 43 odd->fail = odd, even->fail = odd; 44 odd->dif = even->dif = -1, last = even, str[0] = 0; 45 } 46 47 TrieNode* extend(TrieNode* p) { 48 while (str[len - p->len - 1] != str[len]) p = p->fail; 49 return p; 50 } 51 52 void append(char x) { 53 str[++len] = x; 54 int c = x - 'a'; 55 last = extend(last); 56 if (!last->ch[c]) { 57 TrieNode* p = newnode(last->len + 2); 58 p->fail = extend(last->fail)->ch[c]; 59 if (!p->fail) 60 p->fail = even; 61 last->ch[c] = p; 62 p->dif = p->len - p->fail->len; 63 64 if (p->dif == p->fail->dif) 65 p->slink = p->fail->slink; 66 else 67 p->slink = p->fail; 68 } 69 last = last->ch[c]; 70 } 71 }PalindromeTree; 72 73 const int M = 1e9 + 7; 74 75 int n; 76 char bstr[1000005], str[1000005]; 77 PalindromeTree pt; 78 int *f; 79 80 inline void init() { 81 gets(bstr + 1); 82 n = strlen(bstr + 1); 83 for (int i = 1; i <= n; i++) { 84 if (i & 1) 85 str[i] = bstr[(i + 1) >> 1]; 86 else 87 str[i] = bstr[n - (i >> 1) + 1]; 88 } 89 f = new int[(n + 1)]; 90 memset(f, 0, sizeof(int) * (n + 1)); 91 } 92 93 inline void solve() { 94 pt = PalindromeTree(n); 95 f[0] = 1; 96 for (int i = 1; i <= n; i++) { 97 pt.append(str[i]); 98 for (TrieNode* p = pt.last; p && p->len > 0; p = p->slink) { 99 p->g = f[i - p->slink->len - p->dif]; 100 101 if (p->fail->dif == p->dif) 102 p->g = (p->g + p->fail->g) % M; 103 if (!(i & 1)) 104 f[i] = (f[i] + p->g) % M; 105 } 106 } 107 printf("%d", f[n]); 108 } 109 110 int main() { 111 init(); 112 solve(); 113 return 0; 114 }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号