vijos & codevs 能量项链 - 动态规划

描述

在Mars星球上，每个Mars人都随身佩带着一串能量项链。在项链上有N颗能量珠。能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为m，尾标记为r，后一颗能量珠的头标记为r，尾标记为n，则聚合后释放的能量为（Mars单位），新产生的珠子的头标记为m，尾标记为n。

需要时，Mars人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。

例如：设N=4，4颗珠子的头标记与尾标记依次为(2，3) (3，5) (5，10) (10，2)。我们用记号⊕表示两颗珠子的聚合操作，(j⊕k)表示第j，k两颗珠子聚合后所释放的能量。则第4、1两颗珠子聚合后释放的能量为：
(4⊕1)=10*2*3=60。

这一串项链可以得到最优值的一个聚合顺序所释放的总能量为
((4⊕1)⊕2)⊕3）=10*2*3+10*3*5+10*5*10=710。

格式

输入格式

输入文件的第一行是一个正整数N（4≤N≤100），表示项链上珠子的个数。第二行是N个用空格隔开的正整数，所有的数均不超过1000。第i个数为第i颗珠子的头标记（1≤i≤N），当1≤i＜N时，第i颗珠子的尾标记应该等于第i+1颗珠子的头标记。第N颗珠子的尾标记应该等于第1颗珠子的头标记。

至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

输出格式

输出文件只有一行，是一个正整数E（E≤2.1*109），为一个最优聚合顺序所释放的总能量。

样例1

样例输入1

4
2 3 5 10

样例输出1

710

 

限制

1s

来源

NOIP2006第一题

(转自Vijos1312,题目传送门[codevs]&[vijos])

---

　　这道题和加分二叉树有点像，所以立刻想到区间dp。它们俩的差别大概就在一个是树上，还有一个是在环上。处理环就像骑士那样处理，破环成链，特殊处理两端。于是用f[aflag][i][j]来进行dp.

　　（PS，下文的区间指的是项链上的一段,[i, j]表示第i个能量珠到第j个能量珠这一段）

　　其中aflag为0时表示是在链上，[i, j]区间的能量珠合并出来的最大值。当aflag为0时表示过剖开点，从j到i（区间[j, n]和[1, i]）。

　　在链上的比较简单，很容易可以想出方程 f[0][i][j] = max{f[0][i][k] + f[0][k + 1][j] + a[i] * a[k + 1] + a[(j + 1) % n]}(a表示读入的n个数，下标从0开始)

　　过剖开点就有三种情况

1. 

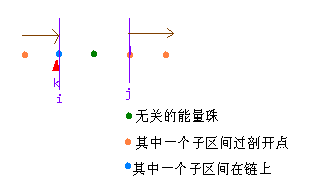
   k在左端，f[1][i][j] = max{f[0][k][i] + f[1][k - 1][j] + a[(i + 1) % n] * a[k] * a[j]}

2. 

    

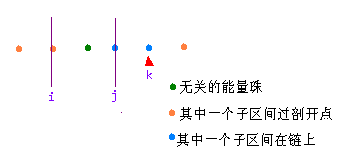
   k在右端，f[1][i][j] = max{f[0][j][k] + f[1][i][k + 1] + a[j] * a[k + 1] * a[(i + 1) % n]}
3. 刚好是两个在链上的区间(区间[j, n]和[1, i])合并，smax(f[1][i][j], f[0][0][i] + f[0][j][n - 1] + a[j] * a[0] * a[i + 1])

 最后在f[0][0][n - 1]和f[1][i][i + 1]中找找最大值就好了。

Code

/**
 * codevs        & vijos.org
 * Problem#1154    & 1312
 * Accepted        & Accepted
 * Time:13ms    & 30ms
 * Memory:364k    & 536k
 */ 
#include<iostream>
#include<sstream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<vector>
#include<algorithm>
using namespace std;
typedef bool boolean;
#define smin(a, b) (a) = min((a), (b))
#define smax(a, b) (a) = max((a), (b))
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        aFlag = -1;
        x = getchar();
    }
    for(u = x - '0'; isdigit((x = getchar())); u = u * 10 + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

template<typename T>class Matrix{
    public:
        T *p;
        int lines;
        int rows;
        Matrix():p(NULL){    }
        Matrix(int rows, int lines):lines(lines), rows(rows){
            p = new T[(lines * rows)];
        }
        T* operator [](int pos){
            return (p + pos * lines);
        }
};
#define matset(m, i, s) memset((m).p, (i), (s) * (m).lines * (m).rows)

#define idx(i)    a[(i + n) % n]

int n;
int *a;
Matrix<int> f[2];

inline void init(){
    readInteger(n);
    f[0] = Matrix<int>(n, n);
    f[1] = Matrix<int>(n, n);
    a = new int[(const int)(n)];
    for(int i = 0; i < n; i++)
        readInteger(a[i]);
}

inline void solve(){
    matset(f[0], 0xf0, sizeof(int));
    matset(f[1], 0xf0, sizeof(int));
    for(int i = 0; i < n - 1; i++){
        f[0][i][i + 1] = a[i] * a[i + 1] * idx(i + 2);
    }
    for(int i = 0; i < n; i++)    f[0][i][i] = 0;
    f[1][0][n - 1] = a[n - 1] * a[0] * a[1];
    for(int s = 2; s < n; s++){
        for(int i = 0; i + s < n; i++){
            int j = i + s;
            for(int k = i; k < j; k++){
                smax(f[0][i][j], f[0][i][k] + f[0][k + 1][j] + a[i] * a[k + 1] * idx(j + 1));
            }
        }
        for(int i = 0; i - s < 0; i++){
            int j = (i - s + n) % n;
            for(int k = i; k > 0; k--){
                smax(f[1][i][j], f[0][k][i] + f[1][k - 1][j] + idx(i + 1) * a[k] * a[j]);
            }
            for(int k = j; k < n - 1; k++){
                smax(f[1][i][j], f[0][j][k] + f[1][i][k + 1] + a[j] * a[k + 1] * idx(i + 1));
            }
            smax(f[1][i][j], f[0][0][i] + f[0][j][n - 1] + a[j] * a[0] * a[i + 1]);
        }
    }
    int result = f[0][0][n - 1];
    for(int i = 0; i < n - 1; i++){
        smax(result, f[1][i][i + 1]);
    }
    cout << result;
}

///Main Funtion
int main(int argc, char* argv[]){
    init();
    solve();
    return 0;
}