NOIP 2018 简要题解
从这里开始
Day 1
Problem A
考虑贪心地选取极大非 0 段减少。
如果两次操作有交,并且不是包含关系,那么把其中一次操作的,但另一次没有操作的移过去,然后就变成了上面那个贪心了。
Code
#include <iostream>
#include <cstdlib>
#include <cstdio>
using namespace std;
typedef bool boolean;
const int N = 1e5 + 5;
int n;
int res = 0;
int ar[N];
inline void init() {
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", ar + i);
}
inline void solve() {
int lst = 0;
for (int i = 1; i <= n; i++) {
if (ar[i] > lst)
res += ar[i] - lst;
lst = ar[i];
}
printf("%d\n", res);
}
int main() {
freopen("road.in", "r", stdin);
freopen("road.out", "w", stdout);
init();
solve();
return 0;
}
Problem B
考虑从小到达确定 $b$ 中的面额。不难发现:
- $b$ 一定是 $a$ 的子集。
- $a$ 中一种面值不在 $b$ 中当且仅当它能被除掉它之后的面额表示出来。
Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
const int N = 105, M = 25005;
int T;
int n, m;
int a[N];
bitset<M> f;
void solve() {
scanf("%d", &n);
m = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
m = max(m, a[i]);
}
sort(a + 1, a + n + 1);
f.reset();
f.set(0);
int ans = 0;
for (int i = 1; i <= n; i++) {
if (!f.test(a[i])) {
for (int j = a[i]; j <= m; j++) {
if (f.test(j - a[i])) {
f.set(j);
}
}
ans++;
}
}
printf("%d\n", ans);
}
int main() {
freopen("money.in", "r", stdin);
freopen("money.out", "w", stdout);
scanf("%d", &T);
while (T--) {
solve();
}
return 0;
}
Problem C
考虑二分答案。考虑在每个子树内决策,每个子树内最多有一条未完成的路径对父节点有贡献。
首先需要最大化数量,不难证明这样不会更劣。
首先已经满足条件的可以直接算入答案,没有满足条件考虑两两配对。这个从大的开始考虑,每次和最小的能够匹配的配对。
考虑如何在数量最大的情况下,最大化对父节点的贡献。考虑最大没有匹配的路径,考虑用它替换掉某组匹配中的较大值。
时间复杂度 $O(n\log V\log n)$。
Code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <vector>
using namespace std;
typedef bool boolean;
template <typename T>
void pfill(T* pst, const T* ped, T val) {
for ( ; pst != ped; *(pst++) = val);
}
typedef class Edge {
public:
int ed, nx, w;
Edge(int ed = 0, int nx = 0, int w = 0):ed(ed), nx(nx), w(w) { }
}Edge;
typedef class MapManager {
public:
int ce;
int* h;
Edge* es;
MapManager() : ce(-1), h(NULL), es(NULL) { }
MapManager(int n, int m) : ce(-1) {
h = new int[(n + 1)];
es = new Edge[(m + 1)];
pfill(h, h + n + 1, -1);
}
void addEdge(int u, int v, int w) {
es[++ce] = Edge(v, h[u], w);
h[u] = ce;
}
Edge& operator [] (int p) {
return es[p];
}
}MapManager;
template <typename T>
class Pool {
public:
int sz;
T *p;
T *tp;
Pool(int sz) : sz(sz) {
p = new T[sz + 1];
tp = p;
}
void reset() {
tp = p;
}
T* alloc(int len) {
T* rt = tp;
tp += len;
// cerr << tp - p << '\n';
return rt;
}
};
typedef pair<int, int> pii;
const int N = 5e4 + 3;
int n, m;
int deg[N];
MapManager g;
Pool<int> pl1(N << 2);
Pool<pii> pl2(N << 2);
Pool<boolean> pl3(N << 2);
inline void init() {
scanf("%d%d", &n, &m);
g = MapManager(n, n << 1);
pfill(deg + 1, deg + n + 1, 0);
for (int i = 1, u, v, w; i < n; i++) {
scanf("%d%d%d", &u, &v, &w);
g.addEdge(u, v, w);
g.addEdge(v, u, w);
deg[u]++, deg[v]++;
}
}
//int cnt;
pii dfs(int p, int fa, int mid) {
int* a = pl1.alloc(deg[p] + 1);
pii* m = pl2.alloc(deg[p] + 1);
boolean* vis = pl3.alloc(deg[p] + 1);
// cerr << ++cnt << '\n';
int rt = 0, tp = 0;
for (int i = g.h[p], e; ~i; i = g[i].nx) {
if ((e = g[i].ed) == fa)
continue;
pii x = dfs(e, p, mid);
rt += x.first, a[++tp] = (x.second + g[i].w);
}
sort(a + 1, a + tp + 1);
while (tp && a[tp] >= mid)
tp--, rt++;
if (!tp)
return pii(rt, 0);
for (int i = 0; i <= tp; i++)
vis[i] = false;
int l = 1, r = tp, _tp = 0;
while (l < r) {
while (l < r && a[l] + a[r] < mid)
l++;
if (l < r) {
m[++_tp] = pii(a[l], a[r]);
vis[l] = vis[r] = true;
l++, r--, rt++;
}
}
while (r && vis[r])
r--;
if (!r)
return pii(rt, 0);
int b = a[r];
for (int i = _tp; i; i--)
if (m[i].first + b >= mid)
return pii(rt, m[i].second);
return pii(rt, b);
}
boolean check(int mid) {
// cnt = 0;
pl1.reset();
pl2.reset();
pl3.reset();
return dfs(1, 0, mid).first >= m;
}
inline void solve() {
int l = 1, r = 5e8, mid;
while (l <= r) {
mid = (l + r) >> 1;
if (check(mid))
l = mid + 1;
else
r = mid - 1;
}
printf("%d\n", l - 1);
}
int main() {
freopen("track.in", "r", stdin);
freopen("track.out", "w", stdout);
init();
solve();
return 0;
}
Day 2
Problem A
暴力枚举断掉环上的哪一条边。
Code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <stack>
using namespace std;
typedef bool boolean;
const int N = 5005;
int n, m;
int tp;
int ans[N];
int cmp[N];
vector<int> g[N];
inline void init() {
scanf("%d%d", &n, &m);
for (int i = 1, u, v; i <= m; i++) {
scanf("%d%d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
}
namespace tree {
void dfs(int p, int fa) {
ans[++tp] = p;
for (int i = 0, e; i < (signed) g[p].size(); i++)
if ((e = g[p][i]) ^ fa)
dfs(e, p);
}
inline void solve() {
tp = 0;
for (int i = 1; i <= n; i++)
sort(g[i].begin(), g[i].end());
dfs(1, 0);
for (int i = 1; i <= n; i++)
printf("%d%c", ans[i], (i == n) ? ('\n') : (' '));
}
}
namespace circle {
stack<int> s;
boolean vis[N];
vector<int> cir;
boolean dfs1(int p, int fa) {
if (vis[p]) {
int cur;
do {
cur = s.top();
s.pop();
cir.push_back(cur);
} while (cur != p);
return true;
}
s.push(p), vis[p] = true;
for (int i = 0, e; i < (signed) g[p].size(); i++)
if (((e = g[p][i]) ^ fa) && dfs1(e, p))
return true;
s.pop();
return false;
}
void dfs(int p, int fa, int banu, int banv) {
cmp[++tp] = p;
// cerr << p << " " << tp << '\n';
boolean sgn1 = (p == banu || p == banv);
for (int i = 0, e; i < (signed) g[p].size(); i++) {
e = g[p][i];
if ((e ^ fa) && !(sgn1 && (e == banu || e == banv)))
dfs(e, p, banu, banv);
}
}
boolean check_update() {
for (int i = 1; i <= n; i++)
if (ans[i] ^ cmp[i])
return cmp[i] < ans[i];
return false;
}
inline void solve() {
for (int i = 1; i <= n; i++)
sort(g[i].begin(), g[i].end());
dfs1(1, 0);
signed int s = (signed) cir.size();
tp = 0;
dfs(1, 0, cir[0], cir[1]);
for (int j = 1; j <= n; j++)
ans[j] = cmp[j];
for (int i = 1; i < s; i++) {
// cerr << cir[i] << '\n';
tp = 0;
dfs(1, 0, cir[i], cir[(i + 1) % s]);
if (check_update())
for (int j = 1; j <= n; j++)
ans[j] = cmp[j];
}
for (int i = 1; i <= n; i++)
printf("%d%c", ans[i], (i == n) ? ('\n') : (' '));
}
}
int main() {
freopen("travel.in", "r", stdin);
freopen("travel.out", "w", stdout);
init();
if (n == m)
circle :: solve();
else
tree :: solve();
return 0;
}
好像校内 oj 上测,最慢一个点 978ms,Emm......
其实考虑在环上每一个位置往回走的下一个标号是确定的。然后就能 $O(n\log n)$ 了。
最近手残得比较厉害,sad.....
Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
const int N = 5e3 + 5;
int n, m;
vector<int> ans;
vector<int> G[N];
void dfs(int p, int fa, vector<int> &ans = ::ans) {
ans.push_back(p);
for (int _ = 0, e; _ < (signed) G[p].size(); _++) {
if ((e = G[p][_]) ^ fa) {
dfs(e, p);
}
}
}
boolean vis[N];
vector<int> cir;
boolean findcir(int p, int fa) {
if (vis[p]) {
vector<int>::iterator it = --cir.end();
while (*it ^ p)
it--;
cir.erase(cir.begin(), it);
return true;
}
vis[p] = true;
cir.push_back(p);
for (int _ = 0, e; _ < (signed) G[p].size(); _++) {
if (((e = G[p][_]) ^ fa) && findcir(e, p)) {
return true;
}
}
cir.pop_back();
return false;
}
void finderase(vector<int>& a, int x) {
vector<int>::iterator it = a.begin();
while (*it ^ x)
it++;
a.erase(it);
}
int main() {
freopen("travel.in", "r", stdin);
freopen("travel.out", "w", stdout);
scanf("%d%d", &n, &m);
for (int i = 1, u, v; i <= m; i++) {
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
for (int i = 1; i <= n; i++)
sort(G[i].begin(), G[i].end());
if (n == m) {
findcir(1, 0);
int nxt = *upper_bound(G[cir[0]].begin(), G[cir[0]].end(), cir[1]);
for (int i = 1, x, y; ; i++) {
x = cir[i];
if (x >= nxt) {
y = cir[i - 1];
finderase(G[x], y);
finderase(G[y], x);
// cerr << x << " " << y << " " << nxt << '\n';
break;
}
vector<int>::iterator it = upper_bound(G[x].begin(), G[x].end(), cir[i + 1]);
if (it != G[x].end() && *it == cir[i - 1])
it++;
if (it != G[x].end())
nxt = *it;
}
}
dfs(1, 0, ans);
for (int i = 0; i < n; i++)
printf("%d ", ans[i]);
return 0;
}
Problem B
请欣赏神仙行为:
- 早上教练发题,神仙 jerome_wei 说难道这题能做,下午发成绩,rk 1 cdqz-wyp 100 100 100 300
- 早上教练发题,神仙 jerome_wei 说咕了咕了,下午发成绩,rk 1 cdqz-wyp 100 100 100 300
- 一天,神仙 jerome_wei 看到了这道题,说这什么鬼题,跑了跑了,不久之后博客上出现了详细题解和证明
不难发现 $a_{x, y} \geqslant a_{x - 1, y + 1}$。
考虑一处不合法的路径,如果存在一定是字典序相邻的一对,这样话就是考虑把最后一个不在最后一行的 R 替换成 D,大概是这样的:
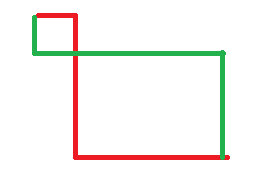
你发现如果第二个位置相等,由于在另一条路径下方的权值一定是小于等于它的,由此可以推出它们字典序相等。那么右下角的大矩形内每一对 $x + y$ 相等的 $a_{x, y}$ 都是相同的。
随便 dp 一下应该能拿到 65 分的好成绩。(枚举 $x + y$ 的值,状压一下当前的满足 $a_{x, y} = a_{x - 1, y + 1}$ 以及横纵坐标和等于 $x + y + 1$ 的状态)
不难注意到,当 $m$ 比较大的时候,中间的有效状态只有常数个,考虑 $x = 0, 1$ 总是可行的,当 $x \geqslant 3, y \geqslant 2$ 的时候,这些格子必须满足 $a_{x, y} = a_{x - 1, y + 1}$。因为:

因为红格子和蓝格子以及蓝格子和黄格子不可能同时都不同。
理论上中间暴力 dp 能过,不过写个矩乘快速幂怎么都能过,我好像有地方写菜了,然后好像就过不了?因为我非常地懒,众所周知,打表可得当 $m \geqslant n + 1$ 的时候当 $m$ 每增加 1,答案乘上 3。
如果我 csp 后没退役再来填这个规律的坑好了。

Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
#define ll long long
void exgcd(int a, int b, int& x, int& y) {
if (!b) {
x = 1, y = 0;
} else {
exgcd(b, a % b, y, x);
y -= (a / b) * x;
}
}
int inv(int a, int n) {
int x, y;
exgcd(a, n, x, y);
return (x < 0) ? (x + n) : (x);
}
const int Mod = 1e9 + 7;
template <const int Mod = :: Mod>
class Z {
public:
int v;
Z() : v(0) { }
Z(int x) : v(x){ }
Z(ll x) : v(x % Mod) { }
friend Z operator + (const Z& a, const Z& b) {
int x;
return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
}
friend Z operator - (const Z& a, const Z& b) {
int x;
return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
}
friend Z operator * (const Z& a, const Z& b) {
return Z(a.v * 1ll * b.v);
}
friend Z operator ~(const Z& a) {
return inv(a.v, Mod);
}
friend Z operator - (const Z& a) {
return Z(0) - a;
}
Z& operator += (Z b) {
return *this = *this + b;
}
Z& operator -= (Z b) {
return *this = *this - b;
}
Z& operator *= (Z b) {
return *this = *this * b;
}
friend boolean operator == (const Z& a, const Z& b) {
return a.v == b.v;
}
};
Z<> qpow(Z<> a, int p) {
Z<> rt = Z<>(1), pa = a;
for ( ; p; p >>= 1, pa = pa * pa) {
if (p & 1) {
rt = rt * pa;
}
}
return rt;
}
typedef Z<> Zi;
#define pii pair<int, int>
const int N = 1e6 + 10;
int n, m;
int Lx[N], Rx[N];
map<pii, Zi> G[N];
int opt(int sum, int s, int x) {
if (x <= Lx[sum] || x > Rx[sum])
return s;
return s | (1 << x);
}
Zi dp(int sum, int s0, int s1) {
if (sum == n + m - 2)
return 2;
if (G[sum].count(pii(s0, s1))) {
return G[sum][pii(s0, s1)];
}
Zi rt = 0;
int ns0 = s1;
for (int i = Lx[sum]; i <= Rx[sum]; i++) {
if ((s0 >> i) & 1) {
ns0 = opt(sum + 1, ns0, i);
ns0 = opt(sum + 1, ns0, i + 1);
}
}
for (int i = Lx[sum]; i <= Rx[sum] + 1; i++) {
if ((s0 >> i) & 1)
continue;
int ns1 = 0;
for (int j = Lx[sum] + 1; j <= i && j <= Rx[sum]; j++)
ns1 = opt(sum + 2, ns1, j + 1);
for (int j = i + 2; j <= Rx[sum]; j++)
ns1 = opt(sum + 2, ns1, j + 1);
rt += dp(sum + 1, ns0, ns1);
}
// cerr << sum << " " << s0 << " " << s1 << " " << rt.v << '\n';
return G[sum][pii(s0, s1)] = rt;
}
Zi solve(int n, int m) {
if (n > m)
swap(n, m);
if (n == m || m == n + 1) {
::n = n, ::m = m;
for (int i = 0; i < m + 10; i++) {
Lx[i] = 20, Rx[i] = 0;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
Lx[i + j] = min(Lx[i + j], i);
Rx[i + j] = max(Rx[i + j], i);
}
}
return dp(0, 0, 0);
}
if (n == 1)
return qpow(2, m);
return solve(n, n + 1) * qpow(3, m - n - 1);
}
int main() {
freopen("game.in", "r", stdin);
freopen("game.out", "w", stdout);
scanf("%d%d", &n, &m);
printf("%d\n", solve(n, m).v);
return 0;
}
Problem C
ddp 板题。
考察选手能否熟练地敲打 ddp 板子。
Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
const int N = 1e5 + 5;
#define ll long long
template <typename T>
T smin(T a, T b) {
return min(a, b);
}
template <typename T, typename ...Q>
T smin(T a, const Q &...args) {
return min(a, smin(args...));
}
const ll llf = 1e12;
typedef class Data {
public:
ll a[2][2];
Data() { }
Data(ll x) {
a[0][0] = llf, a[0][1] = 0;
a[1][0] = x, a[1][1] = x;
}
Data(ll x, ll y, ll z, ll w) {
a[0][0] = x, a[0][1] = y;
a[1][0] = z, a[1][1] = w;
}
Data get() {
ll g = min(a[0][0], a[0][1]);
ll f = min(a[1][0], a[1][1]);
g = min(g, f);
return Data(f, f, g, g);
}
ll* operator [] (int p) {
return a[p];
}
friend Data operator * (Data a, Data b) {
Data rt;
rt[0][0] = min(a[0][0] + b[0][0], a[0][1] + b[1][0]);
rt[0][1] = min(a[0][0] + b[0][1], a[0][1] + b[1][1]);
rt[1][0] = min(a[1][0] + b[0][0], a[1][1] + b[1][0]);
rt[1][1] = min(a[1][0] + b[0][1], a[1][1] + b[1][1]);
return rt;
}
friend Data operator + (Data a, Data b) {
Data rt;
rt[0][0] = a[0][0] + b[0][0];
rt[0][1] = a[0][1] + b[0][1];
rt[1][0] = a[1][0] + b[1][0];
rt[1][1] = a[1][1] + b[1][1];
return rt;
}
friend Data operator - (Data a, Data b) {
Data rt;
rt[0][0] = a[0][0] - b[0][0];
rt[0][1] = a[0][1] - b[0][1];
rt[1][0] = a[1][0] - b[1][0];
rt[1][1] = a[1][1] - b[1][1];
return rt;
}
ll get_ans() {
ll rt = smin(a[0][0], a[0][1], a[1][0], a[1][1]);
return (rt >= llf) ? (-1) : (rt);
}
} Data;
typedef class SegTreeNode {
public:
Data d;
SegTreeNode *fa;
SegTreeNode *l, *r;
void push_up() {
d = l->d * r->d;
}
} SegTreeNode;
typedef class Chain {
public:
SegTreeNode *st;
int len, top;
Chain() { }
Chain(int top);
void update(int, Data, Data);
} Chain;
SegTreeNode pool[N << 1];
SegTreeNode *_top = pool;
int S[N];
Data dat[N];
int tp;
Chain *ch[N];
SegTreeNode *tr[N];
void build(SegTreeNode*& p, int l, int r) {
p = _top++;
if (l == r) {
p->d = dat[S[l]];
tr[S[l]] = p;
return;
}
int mid = (l + r) >> 1;
build(p->l, l, mid);
build(p->r, mid + 1, r);
p->push_up();
p->l->fa = p;
p->r->fa = p;
}
Chain::Chain(int top) : st(_top), len(tp), top(top) {
reverse(S + 1, S + tp + 1);
build(st, 1, len);
for (int i = 1; i <= len; i++) {
ch[S[i]] = this;
}
if (top) {
dat[top] = dat[top] + st->d.get();
}
}
void Chain::update(int x, Data old_d, Data new_d) {
Data nold_d = st->d.get();
tr[x]->d = tr[x]->d - old_d + new_d;
for (SegTreeNode *p = tr[x]->fa; p; p = p->fa)
p->push_up();
if (top) {
ch[top]->update(top, nold_d, st->d.get());
}
}
int n, m;
int p[N];
int sz[N], zson[N];
vector<int> G[N];
void dfs1(int p, int fa) {
int mx = 0, &id = zson[p];
sz[p] = 1;
for (auto e : G[p]) {
if (e ^ fa) {
dfs1(e, p);
sz[p] += sz[e];
if (mx < sz[e]) {
mx = sz[e];
id = e;
}
}
}
}
void dfs2(int p, int fa) {
if (zson[p]) {
for (auto e : G[p]) {
if ((e ^ fa) && (e ^ zson[p])) {
dfs2(e, p);
new Chain(p);
}
}
dfs2(zson[p], p);
} else {
tp = 0;
}
S[++tp] = p;
}
int main() {
freopen("defense.in", "r", stdin);
freopen("defense.out", "w", stdout);
scanf("%d%d%*s", &n, &m);
for (int i = 1, x; i <= n; i++) {
scanf("%d", &x);
dat[i] = x;
p[i] = x;
}
for (int i = 1, u, v; i < n; i++) {
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1, 0);
dfs2(1, 0);
new Chain(0);
int a, x, b, y;
while (m--) {
scanf("%d%d%d%d", &a, &x, &b, &y);
Data olda = p[a], oldb = p[b];
Data na = Data(llf * (1 - x)), nb = Data(llf * (1 - y));
ch[a]->update(a, olda, na);
ch[b]->update(b, oldb, nb);
ll ans = ch[1]->st->d.get_ans() + olda[1][0] * x + oldb[1][0] * y;
ch[a]->update(a, na, olda);
ch[b]->update(b, nb, oldb);
printf("%lld\n", ans);
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号