第十一届山东省大学生程序设计竞赛(热身赛）

B.Willis and Fibonacci Sequence

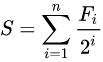
题目：给n，求S；绝对或相对误差小于10^-6

题解：2ⁱ的增长速度大于Fi,当2^k/Fk的值小于10^-6时，因为误差小于10^-6次方，这个值可以忽略不计，当n>=k时，Sn=Sk-1;

#include<bits/stdc++.h>
using namespace std;
#define MAXN 1000000010
typedef long long ll;
int main(){
    int n;
    double sum=0,f1=1,f2=1,f;
    cin>>n;
    if(n==1){
        cout<<"0.50000000"<<endl;
        return 0;
    }
    if(n==2){
        cout<<"0.750000000"<<endl;
        return 0;
    }
    if(n>80){
        n=80;
    }
    sum=0.75;
    for(int i=3;i<=n;i++){
        f=f1+f2;
        f1=f2;
        f2=f;
        sum+=f*1.000000/pow(2,i);
    }
    printf("%.6f\n",sum);
    return 0;
}
//0.5+0.25+3/8

 

C.Mika with Cherry Cake

题意：给出n个商人初始位置(x_i,y_i)以及移动方向dir_i（1为向上，2 为向下，3为向右，4为向左），Mika初始位置为（0，0），Mika和商人在同一地点时可以购买一篮子樱桃，并且Mika买完一次就需要回家放下，求Mika能买到的最大樱桃篮子数。

题解：如果商人能与Mika相遇，那商人一定是离（0，0）越来越近.

1.当dir=1或dir=3时，肯定不能相遇；

2.当dir=2,x>y时,当Mika走到位置x时，商人已经在下方了，所以Mika追不上。同理当dir=2,x>y时，Mika也追不上。只有dir=2,x<=y或者dir=4,y<=x时，商人和Mika才有可能相遇。

储存这些能相遇的情况，排序，优先从与Mika离得近的商人那里购买。t记录Mika从一开始出发的时间，商人和Mika相遇的时间为(x+y-t)/2,Mika取篮子再回去花的时间为x+y-t 。t=t+(x+y-t)

#include<bits/stdc++.h>
using namespace std;
#define MAXN 50010
struct node{
    int x;
    int y;
    int dir;
}a[MAXN];
bool cmp(node a,node b){
    return a.x+a.y<b.x+b.y;
}
int main(){
    int n,cnt=0;
    cin>>n;
    int xx,yy,d;
    for(int i=0;i<n;i++){
        cin>>xx>>yy>>d;
        if(d==1||d==3) continue;
        if(d==2&&xx>yy) continue;
        if(d==4&&yy>xx) continue;
        a[cnt].x=xx,a[cnt].y=yy,a[cnt].dir=d;
        cnt++;
    }
    sort(a,a+cnt,cmp);
    int sum=0,t=0;
    for(int i=0;i<cnt;i++){
        if(a[i].dir==2){
            if(a[i].y-t>=a[i].x){
                sum++;
                t=a[i].x+a[i].y;
                //t=t+a[i].x+a[i].y-t;
            } 
        }else{
            if(a[i].x-t>=a[i].y){
                sum++;
                t=a[i].x+a[i].y;
            } 
        }
    }
    cout<<sum<<endl;
    return 0;
}