2020/6/9习题训练五

A - Sum of Odd Integers

题意：给定两个整数n和k，你的任务是找出n是否可以表示为k个不同的正奇数(不能被2整除)整数的和

题解：前k个最小的奇数的和为sum=1+3+5+.......+2k-1=k*k;如果sum>n,不符合条件；所以如果要n能被k个不同的奇数的和表示需要满足sqrt(n)>k并且k和n同奇同偶

#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,k;
        cin>>n>>k;
        if(k<=sqrt(n)&&((n%2==0&&k%2==0)||(n%2!=0&&k%2!=0))){
            cout<<"YES"<<endl;
        }else{
            cout<<"NO"<<endl;
        }
    }
    return 0;    
} 

B - Princesses and Princes

题意：有n个公主和n个王子，每个公主有心仪的王子，从第一个公主开始给每个公主匹配心仪的王子，如果这n个公主都找到了心仪的对象，输出“OPTIMAL”；如果没有国王会使没有匹配到心仪王子嫁给其他王子，输出“IMPROVE”以及其中一个公主王子的序号

题解：可以用一个数组记录王子是否婚配，如果可以婚配记录cnt++，如果不可以记录此时公主的序号。最后的时候如果cnt等于n，输出“OPTIMAL”，如果不等于输出“IMPROVE”，以及记录的公主的序号和没有婚配的王子。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
#define MAXN 100010
int a[MAXN];
int main(){
     int t;
     cin>>t;
     while(t--){
         int n,cnt=0,girl;
         cin>>n;
         memset(a,0,sizeof(a));
         for(int i=1;i<=n;i++){
             int k,will;
             cin>>k;
             int flag=0;
             for(int j=1;j<=k;j++){
                 cin>>will;
                 if(!a[will]&&!flag){
                     a[will]=1;
                     flag=1,cnt++;
                 }
             }
             if(!flag){
                 girl=i;
             }

         }
        if(cnt==n){
            cout<<"OPTIMAL"<<endl;
        }else{
            cout<<"IMPROVE"<<endl;
            for(int j=1;j<=n;j++){
            if(!a[j]){
                cout<<girl<<" "<<j<<endl;
                break;
            }
        }                
    }
        

     }
         return 0;
} 

C - EhAb AnD gCd

题意：已知一个正整数X，找出任意两个正整数a和b，满足GCD(a,b)+LCM(a,b)=x

题解：使最大公约数为1，那么最小公倍数为x-1；所以让a=1，b=x-1，这样最大公约数只能是1，最小公倍数就是x-1

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int x;
        int a,b;
        cin>>x;
        a=1,b=x-1;
        cout<<a<<" "<<b<<endl;
    }
    return 0;
}

 D - CopyCopyCopyCopyCopy

题意：给含有n个元素的数组a,n个数组a连接成数组b,可以删除多个(可能是零或全部)b中的元素,求最长的递增子序列

题解：实际上就是求数组a中有多少个不同的元素

#include<iostream>
#include<set>
using namespace std;
set<int>s;
int main(){
    int t;
    cin>>t;
    while(t--){
        s.clear();
        int n,num;
        cin>>n;
        for(int i=1;i<=n;i++){
            cin>>num;
            s.insert(num);
        }
        cout<<s.size()<<endl;
    }
    return 0;
}

E - Ehab and Path-etic MEXs

题解：

题意：

F - Yet Another Tetris Problem

题意：给含n个元素的数列a，表示俄罗斯方块每一列的高度。可以对数组中的元素进行两种操作，判断能不能把所有的方块消除

           1.可以从1到到n选择ai,使ai=ai+2        2.如果数组中的元素全部大于零，可以使全部元素减1；

题解：因为可以对元素进行加2处理，所以要使方块全不能被消除，方块的高度只能全部是偶数或者全部是奇数

#include<iostream>
#include<cstring>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,cnt=0,a;
        cin>>n;
        for(int i=1;i<=n;i++){
             cin>>a;
             if(a&1){
                 cnt++;
             }
        }
        if(cnt==n||cnt==0){
            cout<<"YES"<<endl;
        }else{
            cout<<"NO"<<endl;
        }
    }
    return 0;
}

G - Yet Another Palindrome Problem

题意：给由n个元素组成的数组判断数组的子序列中是否有含三个元素的回文序列

子序列定义：如果数组b可以通过从数组a中移除一些(可能是零)元素(不一定是连续的)而不改变其余元素的顺序来获得，则数组b被称为数组a的子序列。

题解：只要判断是否有两个相同的数且这两个数中间隔着一个或一个以上的元素

#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<cmath>
using namespace std;
int a[5010];
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,flag=0;
        cin>>n;
        for(int i=1;i<=n;i++){
            cin>>a[i];
        }
        for(int i=1;i<=n;i++){
            for(int j=i+2;j<=n;j++){
                if(a[i]==a[j]){
                    cout<<"YES"<<endl;
                    flag=1;
                    break;
                }
            }
            if(flag) break;
        }
       if(!flag){
           cout<<"NO"<<endl;
       }
    }
        return 0;
}

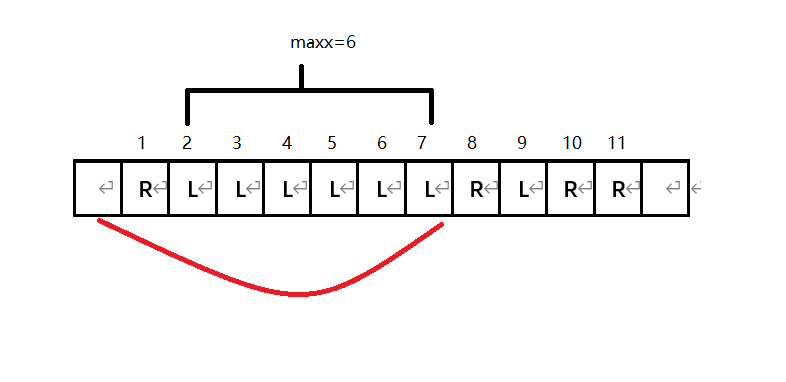
H - Frog Jumps

题意：给一串字符串由"L"和"R"组成，跳到R只能向右跳，跳到到L只能向左跳青蛙想要到达第n + 1个细胞。青蛙在第一次跳跃之前选择一个正整数d(以后不能改变它)，并且一次跳跃不超过d个格子，问你保证能跳到n+1的位置上的情况下，d的最小值；

题解：因为青蛙要往右跳所以要保证它跳到显示L的格子时，不会一直往左跳，所以找到最多有几个连续的L格子，然后加1，保证可以跳过这个最长连续L格；

如果像图中这种情况n=6时跳到L上就一直往左跳，等到了有R的格子上往右跳最大的距离也没用

 

 

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        string s;
        int maxx=0,counts=1;
        cin>>s;
        for(int i=0;i<s.length();i++){
            if(s[i]=='L'){
                counts=1;
                while(s[i]=='L'){
                    counts++;
                    i++;
                }
            }
                maxx=max(counts,maxx);
        }
        cout<<maxx<<endl;
    }
        return 0;
}