2020/3/14 Preliminaries for Benelux Algorithm Programming Contest 2019 部分补题报告和解题报告
A. Architecture
比较行列最大值相同则possible 不同则impossible
#include<iostream> #include<algorithm> #include<cmath> #include<cstdio> using namespace std; int main(){ int r,c,x,y,i; int maxx=0,maxy=0; cin>>r>>c; for(i=1;i<=r;i++){ cin>>x; maxx=max(x,maxx); } for(i=1;i<=c;i++){ cin>>y; maxy=max(maxy,y); } if(maxx==maxy){ cout<<"possible"<<endl; }else{ cout<<"impossible"<<endl; } return 0; }
B Bracket Sequence
题意:
给定一个带括号的串,求运算结果,结果对1e9+7取模。
第一层括号外数相加,第一层到第二层为相乘,然后交替运算,给定n,输入n个字符(数字或左右括号)
#include<iostream> #include<cstring> #include<cstdio> #include<string> using namespace std; typedef long long ll; #define maxn 300000+5 const int mod=1e9+7; ll st[maxn],top,cnt; //定义为全局变量 自动赋值为零 int n; char op[20]; ll get(char *s){ int len=strlen(s); ll x = 0; for(int i=0;i<len;i++){ x=x*10+s[i]-'0'; //把字符串如12 变成数12 } return x; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%s",op); if(op[0]=='('){ cnt++; st[++top] = -1; continue; }else if(op[0]==')'){ if(st[top]==-1){ top--; continue; } ll x=st[top]; //top为第几个'(' while(top>=2&&st[top-1]!=-1){ if(cnt%2==0) x=(st[top-1]+x)%mod; else x=(st[top-1])*x%mod;
top--; } cnt--; top-=2; st[++top] = x; }else{ ll x =get(op); st[++top]=x; } } ll res = 0; while(top) res=(res+st[top--])%mod; printf("%lld\n",res); return 0; }
D. Deceptive Dice
你有一个n个面的骰子,各面分别有1,2,3……,n 点;一开始你转动骰子,然后你有两个选择:
- 让骰子停止转动;
- 重新转动骰子.
你最多可以转动 k次骰子,你的得分为让骰子停止后骰子的点数,求分数的期望值.
一开始转动骰子,期望值显然是: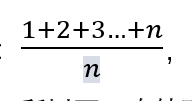 ,记作E1
,记作E1
我们认为期望一定是最优的策略,所以下一次转动骰子的期望分为两部分:
- 点数小于等于上一次的期望值,那么这时认为最优的策略是停下,期望值为
![]()
- 点数大于上一次的期望值,认为继续转是最优的策略,期望:
![]()
所以转移就是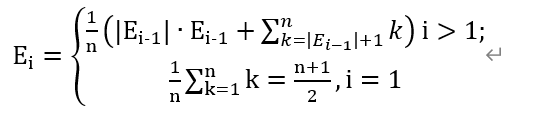
#include<cstdio> #include<iostream> #include<cmath> #include<algorithm> using namespace std; int main(){ double n,ans=0,t=0; int k; cin>>n>>k; while(k--){ ans=(ans*t+n*(n+1)/2-t*(t+1)/2)/n; t=floor(ans); //函数返回参数不大于ans的最大整数。
} printf("%.9f\n",ans); return 0; }
F. Floor Plan
题意:
给 n 判断是否存在m,k使 n = m^2 - k^2 ,即n = (m+k)(m-k),存在则输出吗,m,k ,不存在则impossible,根据数学,可知若 c = a+b,d =a-b;则 a= (c+d)/2; b = (c-d)/2;
从1开始到sqrt (n)+1 ,从中找n的因子,可以求得 n =因子*(n/因子),即n = a*b a即两数和 b即两数差 求(a+b)/2, (a-b)/2 因为可能不被二整除 若(a+b)/2+(a-b)/2==a
且(a+b)/2 - (a-b)/2==b,则m=(a+b)/2, k=(a-b)/2;
sqrt(n) 是因为 a b 都在 0 和 n 之间 +1是因为会被省掉小数的部分
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; int main(){ int n; long long m,k,i,j,a,b; scanf("%d",&n); for(i=1;i<=sqrt(n)+1;i++){ if(n%i==0){ a=n/i; b=i; m=(a+b)/2; k=(a-b)/2; if((m+k)==a&&(m-k)==b&&(a-b)>=0){ printf("%lld %lld\n",m,k); return 0; } } } printf("impossible"); return 0; }
G. Greetings!
把字符串中的e双倍输出
#include<iostream> #include<string> #include<cstring> #include<cstdio> using namespace std; char s[1010]; int main(){ string a; cin>>s; for(int i=0;i<strlen(s);i++){ a+=s[i]; if(s[i]=='e') a+='e'; } cout<<a<<endl; return 0; }
I. Inquiry I
给定n个正整数a1,…, an,判断下面式子的最大值是多少
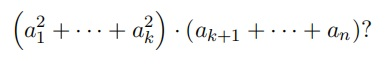
#include<iostream> #include<algorithm> #include<cmath> #include<cstdio> using namespace std; #define MAXN 1000010 long long a[MAXN],b[MAXN]; int main(){ int n,num; scanf("%d",&n); long long maxx=0; for(int i=1;i<=n;i++){ scanf("%d",&num); a[i]+=a[i-1]+num*num; //计算前i个数的平方和 b[i]+=b[i-1]+num; //计算前i个数的和 } for(int i=1;i<n;i++){ maxx=max(maxx,a[i]*(b[n]-b[i])); } printf("%lld\n",maxx); return 0; }


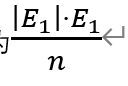
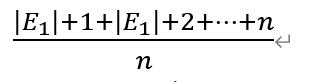

 浙公网安备 33010602011771号
浙公网安备 33010602011771号