(转)样本方差的期望
著作权归作者所有。
商业转载请联系作者获得授权,非商业转载请注明出处。
作者:魏天闻
链接:http://www.zhihu.com/question/20099757/answer/26586088
来源:知乎
商业转载请联系作者获得授权,非商业转载请注明出处。
作者:魏天闻
链接:http://www.zhihu.com/question/20099757/answer/26586088
来源:知乎
首先,我们假定随机变量 的数学期望
的数学期望 是已知的,然而方差
是已知的,然而方差 未知。在这个条件下,根据方差的定义我们有
未知。在这个条件下,根据方差的定义我们有
![\mathbb{E}\Big[\big(X_i -\mu\big)^2 \Big]=\sigma^2, \quad\forall i=1,\ldots,n,](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cbig%28X_i+-%5Cmu%5Cbig%29%5E2+%5CBig%5D%3D%5Csigma%5E2%2C+%5Cquad%5Cforall+i%3D1%2C%5Cldots%2Cn%2C)
由此可得
![\mathbb{E}\Big[\frac{1}{n} \sum_{i=1}^n\Big(X_i -\mu\Big)^2 \Big]=\sigma^2](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cmu%5CBig%29%5E2+%5CBig%5D%3D%5Csigma%5E2) .
.
因此 是方差
是方差 的一个无偏估计,注意式中的分母不偏不倚正好是
的一个无偏估计,注意式中的分母不偏不倚正好是 !
!
这个结果符合直觉,并且在数学上也是显而易见的。
现在,我们考虑随机变量 的数学期望
的数学期望 是未知的情形。这时,我们会倾向于无脑直接用样本均值
是未知的情形。这时,我们会倾向于无脑直接用样本均值 替换掉上面式子中的
替换掉上面式子中的 。这样做有什么后果呢?后果就是,
。这样做有什么后果呢?后果就是,
如果直接使用 作为估计,那么你会倾向于低估方差!
作为估计,那么你会倾向于低估方差!
这是因为:
![\begin{eqnarray}
\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2 &=&
\frac{1}{n}\sum_{i=1}^n\Big[(X_i-\mu) + (\mu -\bar{X}) \Big]^2\\
&=&
\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2
+\frac{2}{n}\sum_{i=1}^n(X_i-\mu)(\mu -\bar{X})
+\frac{1}{n}\sum_{i=1}^n(\mu -\bar{X})^2 \\
&=&
\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2
+2(\bar{X}-\mu)(\mu -\bar{X})
+(\mu -\bar{X})^2 \\
&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2
-(\mu -\bar{X})^2
\end{eqnarray}](http://zhihu.com/equation?tex=%5Cbegin%7Beqnarray%7D%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cbar%7BX%7D%29%5E2+%26%3D%26%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%5CBig%5B%28X_i-%5Cmu%29+%2B+%28%5Cmu+-%5Cbar%7BX%7D%29+%5CBig%5D%5E2%5C%5C%0A%26%3D%26%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%5E2+%0A%2B%5Cfrac%7B2%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%28%5Cmu+-%5Cbar%7BX%7D%29%0A%2B%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28%5Cmu+-%5Cbar%7BX%7D%29%5E2+%5C%5C%0A%26%3D%26%0A%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%5E2+%0A%2B2%28%5Cbar%7BX%7D-%5Cmu%29%28%5Cmu+-%5Cbar%7BX%7D%29%0A%2B%28%5Cmu+-%5Cbar%7BX%7D%29%5E2+%5C%5C%0A%26%3D%26%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5En%28X_i-%5Cmu%29%5E2+%0A-%28%5Cmu+-%5Cbar%7BX%7D%29%5E2+%0A%5Cend%7Beqnarray%7D)
换言之,除非正好 ,否则我们一定有
,否则我们一定有
 ,
,
而不等式右边的那位才是的对方差的“正确”估计!
这个不等式说明了,为什么直接使用 会导致对方差的低估。
会导致对方差的低估。
那么,在不知道随机变量真实数学期望的前提下,如何“正确”的估计方差呢?答案是把上式中的分母 换成
换成 ,通过这种方法把原来的偏小的估计“放大”一点点,我们就能获得对方差的正确估计了:
,通过这种方法把原来的偏小的估计“放大”一点点,我们就能获得对方差的正确估计了:
![\mathbb{E}\Big[\frac{1}{n-1} \sum_{i=1}^n\Big(X_i -\bar{X}\Big)^2\Big]=\mathbb{E}\Big[\frac{1}{n} \sum_{i=1}^n\Big(X_i -\mu\Big)^2 \Big]=\sigma^2.](http://zhihu.com/equation?tex=%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn-1%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cbar%7BX%7D%5CBig%29%5E2%5CBig%5D%3D%5Cmathbb%7BE%7D%5CBig%5B%5Cfrac%7B1%7D%7Bn%7D+%5Csum_%7Bi%3D1%7D%5En%5CBig%28X_i+-%5Cmu%5CBig%29%5E2+%5CBig%5D%3D%5Csigma%5E2.)
至于为什么分母是 而不是
而不是 或者别的什么数,最好还是去看真正的数学证明,因为数学证明的根本目的就是告诉人们“为什么”;暂时我没有办法给出更“初等”的解释了。
或者别的什么数,最好还是去看真正的数学证明,因为数学证明的根本目的就是告诉人们“为什么”;暂时我没有办法给出更“初等”的解释了。
由此可得
因此
这个结果符合直觉,并且在数学上也是显而易见的。
现在,我们考虑随机变量
如果直接使用
这是因为:
换言之,除非正好
而不等式右边的那位才是的对方差的“正确”估计!
这个不等式说明了,为什么直接使用
那么,在不知道随机变量真实数学期望的前提下,如何“正确”的估计方差呢?答案是把上式中的分母
至于为什么分母是
=================================下面是证明===============================================
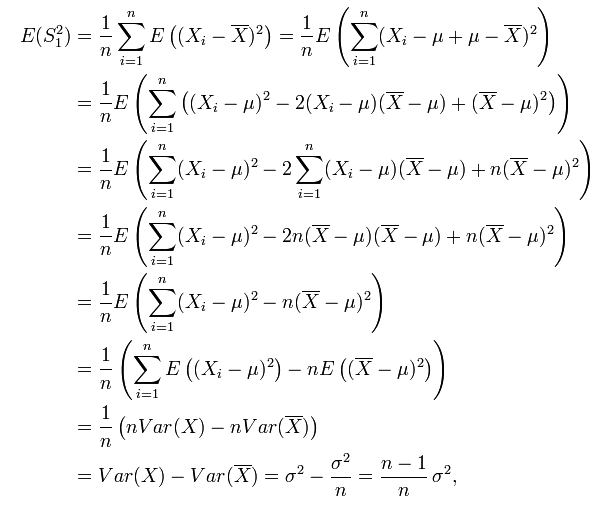




 浙公网安备 33010602011771号
浙公网安备 33010602011771号