深入解析：Metal - 5.深入剖析 3D 变换

在第四章中，我们通过在顶点函数中简单地计算位置数据，实现了模型的位移。但如果要在 3D 空间中执行更复杂的任务，例如旋转和缩放，并最终引入场景中的摄影机，矩阵（Matrices）是不可或缺的工具。

本章将详细讲解如何使用矩阵来实现这些 3D 变换。一旦掌握了对单个三角形的矩阵操作，将其扩展到包含数千个顶点的模型将非常简单。

---

一、 变换概述（Transformations）

变换（Transformations） 是对 3D 几何图形进行操作的过程。本章讨论的变换属于 仿射变换（Affine Transformations），这意味着在应用变换后，所有平行线依然保持平行。

核心的 3D 变换包括：位移（Translation）、缩放（Scale）和旋转（Rotation）。

二、 位移（Translation）

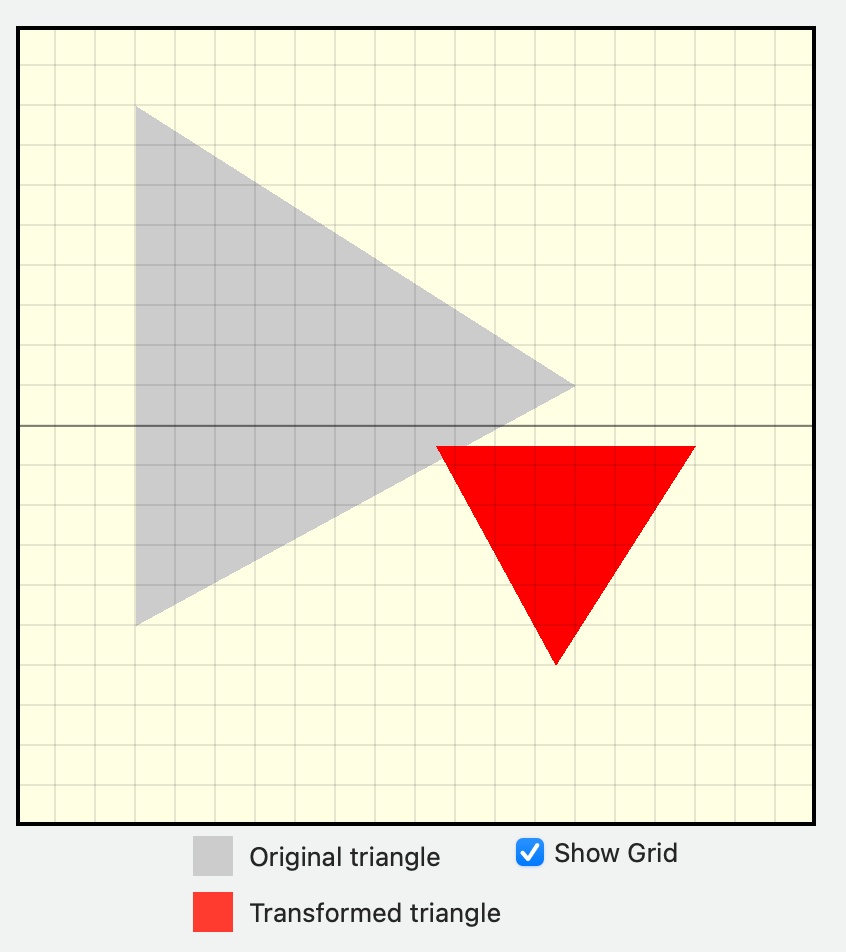
在第四章中，我们通过简单地将位移向量添加到顶点位置来实现位移。然而，在现代计算机图形学中，更常见的方法是：将包含模型当前位置、旋转和缩放信息的矩阵发送给顶点着色器。

1. 创建矩阵（Creating a Matrix）

在 Metal 中，变换操作通过 $4\times 4$ 矩阵来实现。

• 单位矩阵（Identity Matrix）：这是所有变换的起点。它是一个 4x4 矩阵，主对角线上的元素是 $1$，其余元素为 $0$。
  • 在 Swift 端，我们定义一个 matrix_float4x4 并初始化为单位矩阵。
• 位移向量：在 4x4 矩阵中，位移向量（$x,y,z$）存储在矩阵的第四列的 $x,y,z$ 分量中。

将矩阵发送到着色器：

1. Swift 端：使用 renderEncoder.setVertexBytes 将 matrix_float4x4 类型的 matrix 发送到缓冲区索引 11。
2. 着色器端：顶点函数通过 [[buffer(11)]] 限定符接收 constant float4x4 &matrix。

2. 矩阵乘法应用

为了将位移应用于顶点，着色器将从简单相加改为执行矩阵乘法：

$$\text{translation}=\text{matrix}\times \text{in.position}$$

此时，in.position（顶点原始位置）被视为一个 $4\times 1$ 的向量，并与 $4\times 4$ 的变换矩阵相乘。

var vertices: [Float] = [
-0.7,  0.8,  0,
-0.7, -0.5,  0,
0.4,  0.1,  0
]
let translateX: Float = 0.3
let translateY: Float = -0.4
let translationMatrix = float4x4(
[1, 0, 	0,	0],
[0,	1,	0,	0],
[0,	0, 	1, 	0],
[translateX, translateY, 	0, 1])

注意，OpenGL、Metal 以及 Swift 的 SIMD 库都使用列主序存储，因为计算机的内存是一维的、线性的，所以 [translateX, translateY, 0, 1] 其实对应的是第四列。

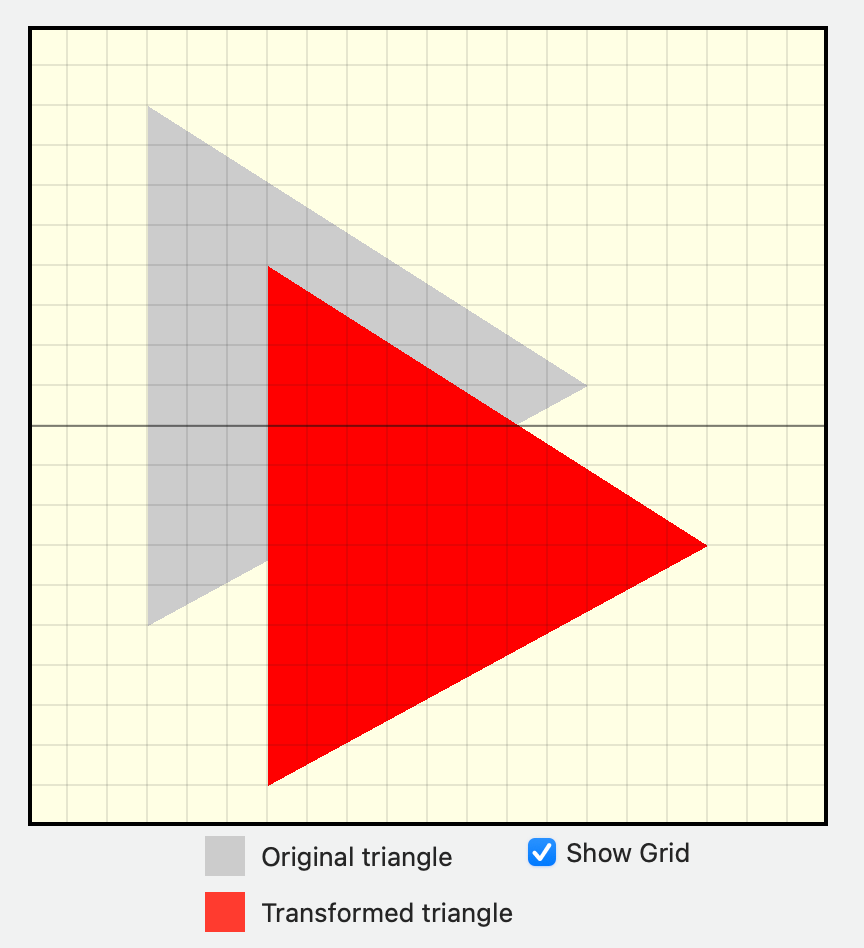
三、 缩放（Scaling）

缩放操作的实现与位移类似，但其值位于矩阵的不同位置。

• 缩放矩阵的结构：缩放因子位于矩阵的对角线上。例如，要在 $X,Y,Z$ 轴上分别缩放 $\text{Sx},\text{Sy},\text{Sz}$，只需将它们放置在矩阵第一、第二和第三列的对角线位置。
• 组合变换：要实现缩放后的位移，需要将位移矩阵乘以缩放矩阵。在 Metal 的矩阵乘法中，顺序很重要。例如，matrix = translation * scaleMatrix 会将缩放后的三角形进行位移。

let scaleX: Float = 0.5
let scaleY: Float = 0.5
let scaleMatrix = float4x4(
[scaleX, 0, 	0,  0],
[0, scaleY,	0,	0],
[0, 			0, 	1, 	0],
[0, 			0, 	0,  1])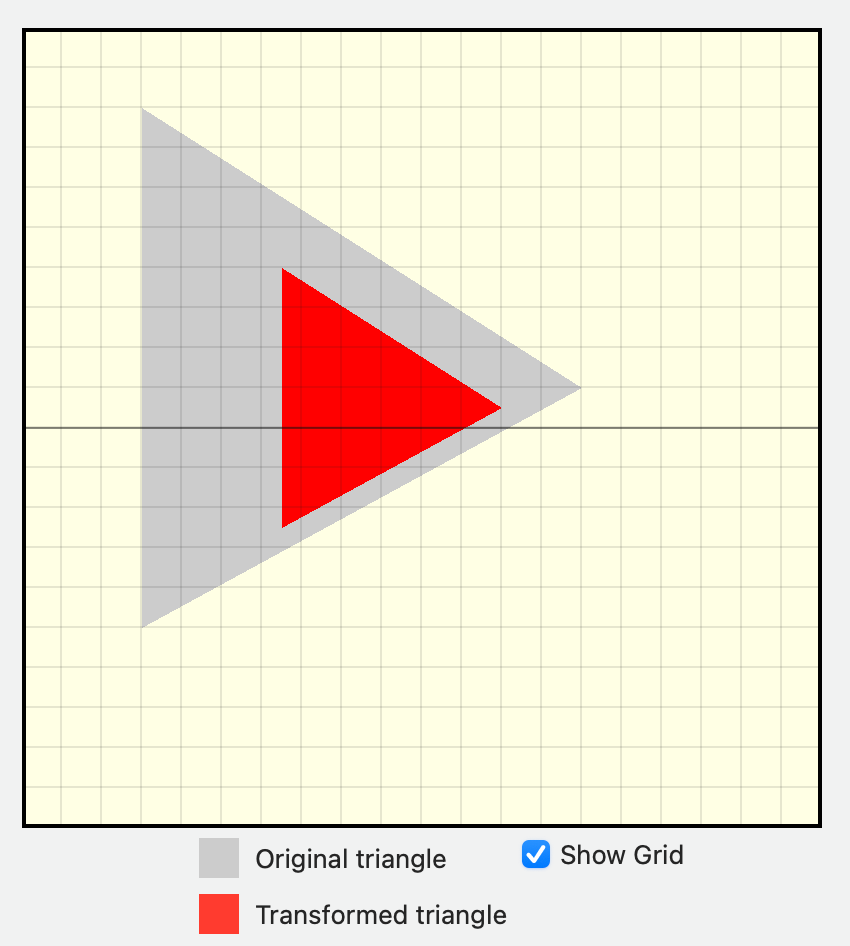

四、 旋转（Rotation）

旋转操作的实现方式与缩放类似。

• 旋转矩阵：通常围绕 Z 轴定义旋转角度。
• 单位：计算机图形学中，标准单位是 弧度（radians）。Metal 使用 Float.pi / 2.0 来表示 $90^{\circ }$。
• 绕原点旋转：默认的旋转矩阵操作总是围绕 原点 $$ 进行。

let angle = Float.pi / 2.0
let rotationMatrix = float4x4(
[cos(angle), -sin(angle), 0, 	0],
[sin(angle), cos(angle),  0, 	0],
[0, 					0, 				  1, 	0],
[0, 					0, 					0, 	1])

注意，Metal 是左手坐标系，从观察者视角来看，是顺时针旋转，但是从z轴方向看（人站在z轴正方向无穷远处顺着负方向看）是逆时针旋转。

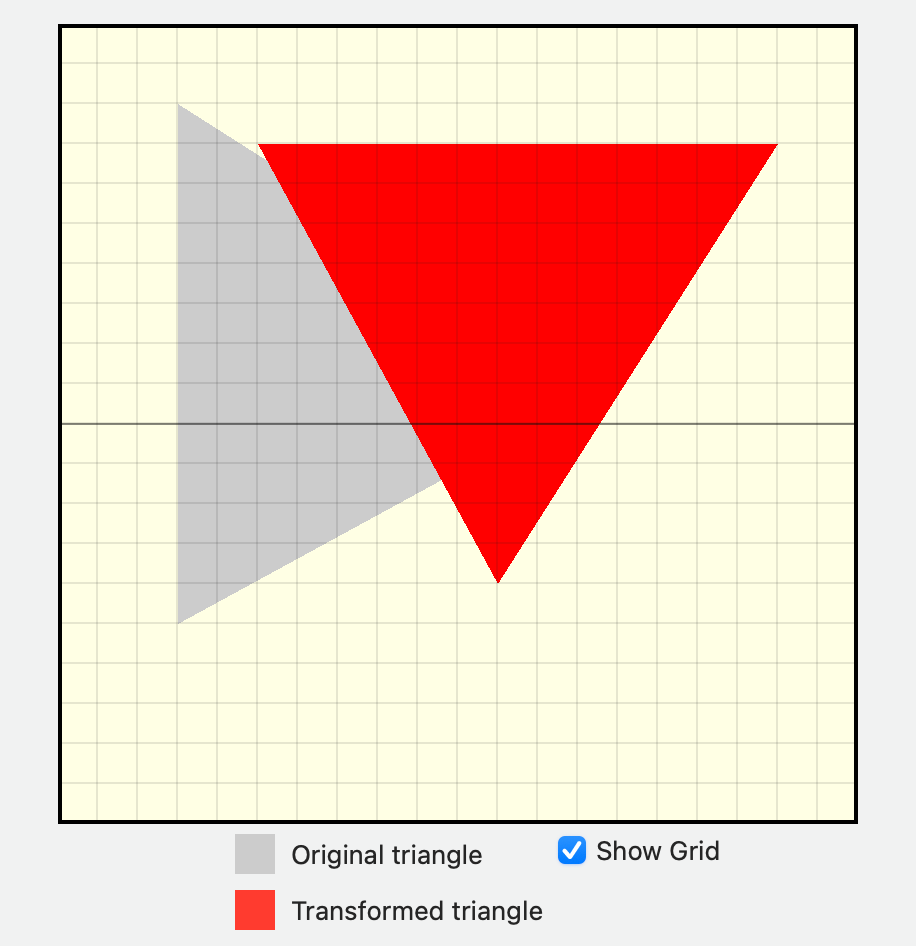
绕任意点旋转（Rotation About a Point）

如果需要围绕模型的某个特定点（而不是原点）进行旋转，需要一个三步序列的组合变换：

1. 平移到原点：使用位移矩阵 $T^{-1}$ 将旋转中心点移动到原点。
2. 旋转：应用旋转矩阵 $R$。
3. 平移回去：应用逆位移矩阵 $T$ 将所有点移回原位。

最终的变换矩阵是这三个操作的乘积：

$$\text{Final Matrix}=T\times R\times T^{-1}$$

在 Swift/Metal 中实现此操作时，需要首先计算出将目标旋转点移动到原点所需的位移矩阵 $T$，然后通过调用 translation.inverse 来获取 $T^{-1}$。

---

五、 组合

1. scaleMatrix * rotationMatrix * translationMatrix
   
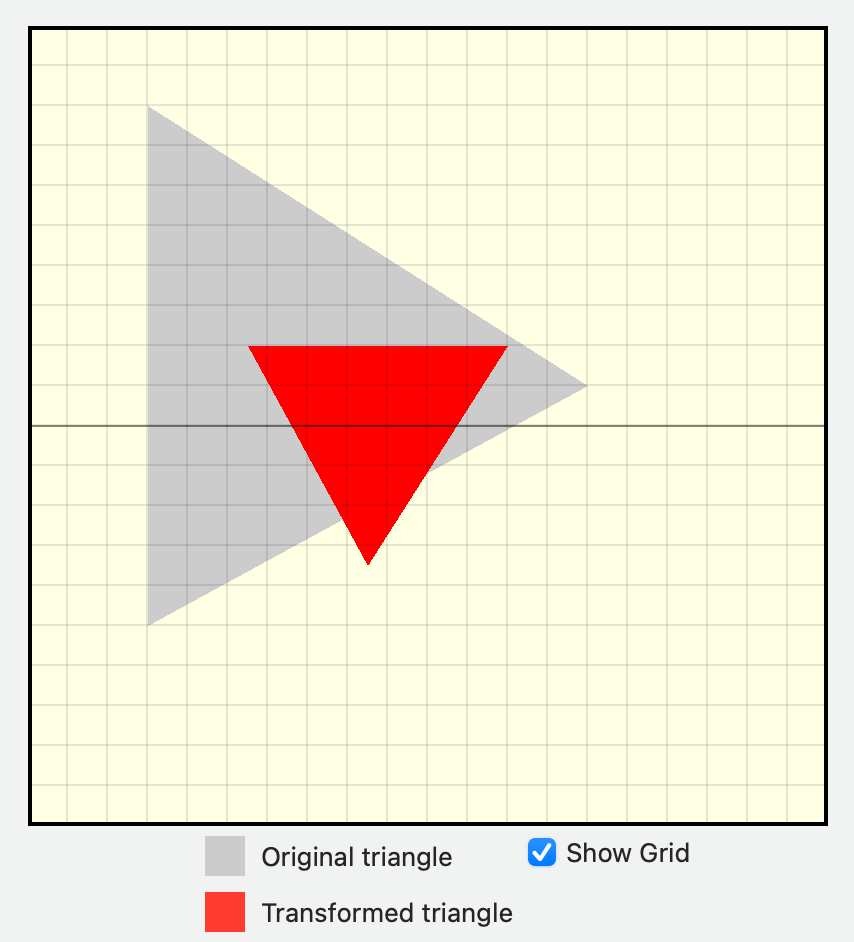
2. translationMatrix * rotationMatrix * scaleMatrix

六、 Metal 变换总结（Key Points）

• 向量与矩阵：向量是只有一行或一列的矩阵。
• 组合变换：通过组合位移、旋转和缩放这三个矩阵，可以将模型定位在场景中的任何位置。
• 顶点函数：顶点函数负责接收这个组合变换矩阵，并通过矩阵乘法计算出每个顶点在裁剪空间中的最终位置。
• 数学基础：虽然 Metal API 抽象了大部分数学细节，但理解线性代数（特别是向量和矩阵的视觉意义）对于创造性地使用变换至关重要。

---

七、 Metal 与 OpenGL 变换概念对比

Metal 和 OpenGL 在实现 3D 变换时，核心数学原理（矩阵乘法）是相同的，但 API 级别上存在显著的工具和哲学差异。

概念	Metal (SIMD, MSL)	OpenGL (GLM, GLSL)	核心差异
数学库	依赖于 Apple 的 SIMD 框架（如 matrix_float4x4）和 Metal Shading Language (MSL) 的内置类型。	依赖于第三方数学库，最常见的是 GLM (OpenGL Mathematics)。GLM 是专为 OpenGL 定制的头文件库，提供了矩阵和向量操作。	Metal 自带数学类型；OpenGL 需要外部库。
矩阵定义	矩阵和向量类型在 Swift 和 MSL 中原生支持（例如 float4x4）。	GLSL 提供了 mat4 和 vec4 等类型。C++ 主程序通常使用 GLM 定义 glm::mat4。
矩阵传输	矩阵通常通过 renderEncoder.setVertexBytes 或作为 MTLBuffer 中的 Uniforms 结构体发送到着色器。	矩阵通过 Uniform 变量发送到 GLSL 着色器。需要使用如 glUniformMatrix4fv 这样的函数来发送数据。
矩阵乘法	在 MSL 顶点函数中执行乘法：float4 position = matrix * in.position。	在 GLSL 顶点着色器中执行乘法：gl_Position = transform * vec4(aPos, 1.0f)。
变换顺序	组合变换需要遵循正确的矩阵乘法顺序，通常是 $T\times R\times S$ (如果顶点是从右向左乘)。	OpenGL 中同样需要遵循矩阵乘法顺序，例如：projection * view * model。GLM 自动将连续的操作相乘，但开发者仍需注意函数调用的顺序。
渲染位置输出	顶点函数将最终结果输出到 VertexOut 结构体中的 [[position]] 属性。	顶点着色器将结果赋值给内置变量 gl_Position。
NDC 空间	Metal NDC 的 $Z$ 轴范围是 $0$ 到 $1$。	OpenGL NDC 的 $X,Y,Z$ 轴范围都是 $-1.0$ 到 $1.0$。