基本需求:D在样本空间中找到一个划分超平面、将不同类别的样本分开理想中的超平面:该划分超平面对训练样本局部扰动的“容忍性”最好优化目标:最大化margin注:找支持向量机越近越好而d越大越好超平面:超平面H是从n维空间到n-1维空间的一个映射子空间,它有一个n维向量和一个实数定义。如果空间是三维的,那么它的超平面是二维平面,而若是空间是二维的,则其超平面是一维直线。超平面行使用
介绍
基本需求:D在样本空间中找到一个划分超平面、将不同类别的样本分开
理想中的超平面:该划分超平面对训练样本局部扰动的“容忍性”最好
优化目标:最大化margin
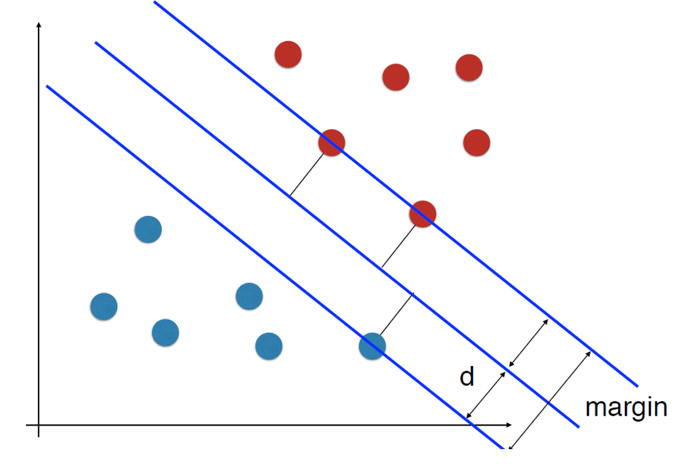
注:找支持向量机越近越好而d越大越好
超平面:超平面H是从n维空间到n-1维空间的一个映射子空间,它有一个n维向量和一个实数定义。
如果空间是三维的,那么它的超平面是二维平面,而如果空间是二维的,则其超平面是一维直线。
超平面许可使用方程表
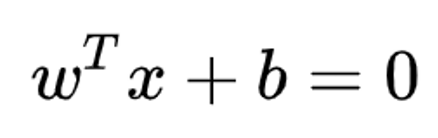
核心概念:
支持向量 (Support Vectors):文档明确提到了这个概念,它是SVM的核心元素(尽管文档未定义)。
超平面 (Hyperplane):一个n-1维的子空间。就是定义:在n维空间中,超平面表示:行用一个方程定义(例如,在三维空间是二维平面,在二维空间是一维)
距离:提到了点到超平面的距离(这是计算间隔的基础)。
应用
# 导入额外的朴素贝叶斯模型
from sklearn.naive_bayes import MultinomialNB, BernoulliNB
from sklearn.preprocessing import MinMaxScaler
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
# 1. 高斯朴素贝叶斯(已训练)
print("高斯朴素贝叶斯模型:")
print(f"准确率: {accuracy:.4f}")
# 2. 多项式朴素贝叶斯(需要非负特征)
print("\n训练多项式朴素贝叶斯模型...")
# 创建MinMaxScaler将特征缩放到[0,1]范围
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 创建并训练多项式朴素贝叶斯模型
mnb_model = MultinomialNB()
mnb_model.fit(X_train_scaled, y_train)
# 评估多项式朴素贝叶斯
y_pred_mnb = mnb_model.predict(X_test_scaled)
accuracy_mnb = accuracy_score(y_test, y_pred_mnb)
print(f"多项式朴素贝叶斯准确率: {accuracy_mnb:.4f}")
# 3. 伯努利朴素贝叶斯(需要二值特征)
print("\n训练伯努利朴素贝叶斯模型...")
# 将特征二值化(大于0为1,否则为0)
X_train_binary = np.where(X_train > 0, 1, 0)
X_test_binary = np.where(X_test > 0, 1, 0)
# 创建并训练伯努利朴素贝叶斯模型
bnb_model = BernoulliNB()
bnb_model.fit(X_train_binary, y_train)
# 评估伯努利朴素贝叶斯
y_pred_bnb = bnb_model.predict(X_test_binary)
accuracy_bnb = accuracy_score(y_test, y_pred_bnb)
print(f"伯努利朴素贝叶斯准确率: {accuracy_bnb:.4f}")
# 4. 支持向量机模型
print("\n训练支持向量机模型...")
# SVM对特征缩放敏感,因此先进行标准化
scaler_svm = StandardScaler()
X_train_svm = scaler_svm.fit_transform(X_train)
X_test_svm = scaler_svm.transform(X_test)
# 创建并训练支持向量机模型
svm_model = SVC(kernel='rbf', probability=True, random_state=42)
svm_model.fit(X_train_svm, y_train)
# 评估支持向量机
y_pred_svm = svm_model.predict(X_test_svm)
accuracy_svm = accuracy_score(y_test, y_pred_svm)
print(f"支持向量机准确率: {accuracy_svm:.4f}")
# 比较四种模型的准确率
models = {
'高斯朴素贝叶斯': accuracy,
'多项式朴素贝叶斯': accuracy_mnb,
'伯努利朴素贝叶斯': accuracy_bnb,
'支持向量机': accuracy_svm
}
# 可视化比较结果
plt.figure(figsize=(12, 6))
plt.bar(models.keys(), models.values(), color=['blue', 'green', 'red', 'purple'])
plt.title('四种分类模型准确率比较')
plt.ylabel('准确率')
plt.ylim(0.7, 0.9)
plt.grid(axis='y', alpha=0.3)
# 在柱子上方添加准确率数值
for i, (model, acc) in enumerate(models.items()):
plt.text(i, acc + 0.005, f"{acc:.4f}", ha='center', fontsize=10)
plt.show()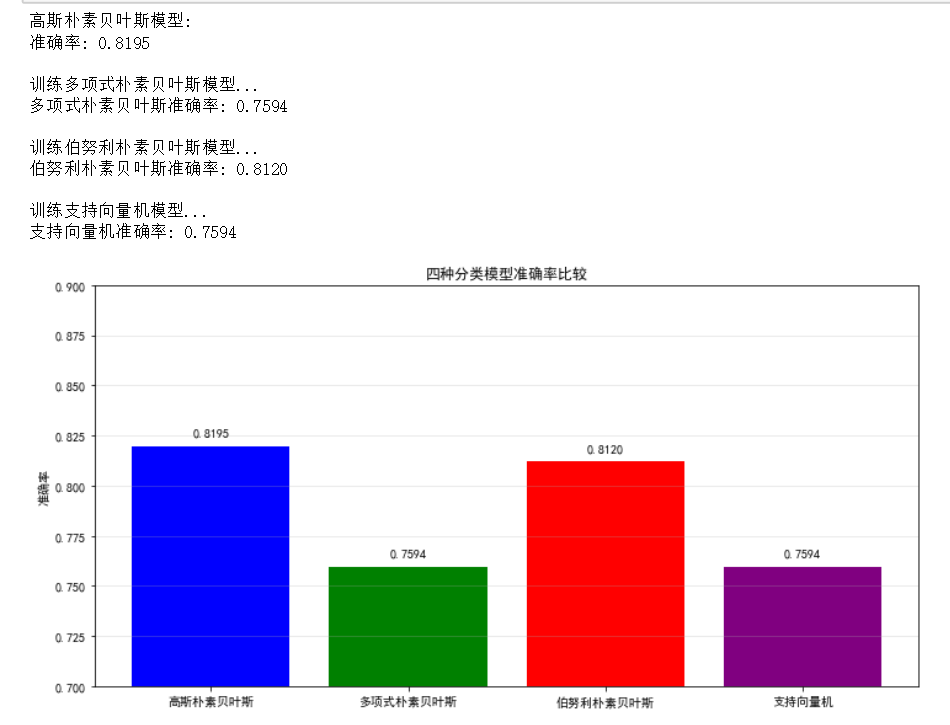





 浙公网安备 33010602011771号
浙公网安备 33010602011771号