信息的表示和处理

 1.1计算机中的存储单元

在操作系统虚拟内存技术的处理下，机器级程序将内存视为一个很大的字节数组，称为虚拟内存。

虚拟内存的最小寻址单元是字节（byte=8bit），每个字节都由一个唯一的固定字长的数字标识称为地址。这些地址的集合，称为虚拟地址空间。

1.1.1计算机的字长属性

每台计算机都有一个字长属性，指明指针数据的标称大小。因为虚拟内存是通过字长编码表示地址的，所以字长决定的最重要的参数就是虚拟内存的最大寻址大小。32位机限制的虚拟内存空间为4GB，64位机限制的虚拟内存空间为16EB。另一方面字长也决定总线数据传输的定长大小。

1.1.2寻址和字节顺序

对于跨越多字节的程序对象，我们必须建立两个规则：“这个对象的地址是什么，对象在多字节中的排列顺序”。

多字节对象都存储在连续的字节序列，对象的地址使用字节中最小的地址，存储方式是没有区别的，但是字节顺序存在大端与小端的区别。

假设变量x的类型为int，位于地址0x100处，在内存中占四个字节，它的十六进制值为0x01234567。x的位表示为[01,23,45,67],其中‘01’就叫做最高有效位，‘67’叫做最低有效位。

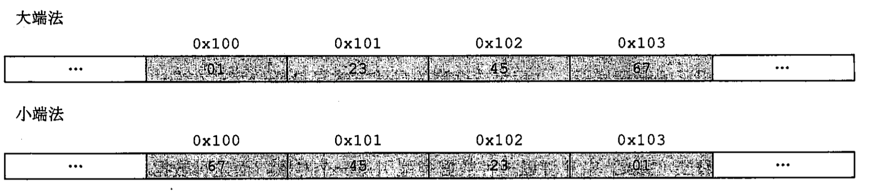
小端存储：最低有效字节放在小地址。

大端存储：最高有效字节放在小地址。

大多数Intel兼容机都只用小端模式，另一方面，IBM和Oracle 2010年收购Sun的大多数机器是大端模式。Android和iOS只能运行于小端模式。

通过上图ubuntu对int 数据0x1234567的存储看到，ubuntu的最低有效位在小地址。所依ubuntu系统采取的是小端模式。

其中汉字采取了UTF-8的编码。（字符，字符集，字符编码——了解字符集与编码的区别）

1.1.3布尔代数简介

二进制值是计算机编码、存储和操作信息的核心，围绕着数值0和1的研究也演化了丰富的数学体系。

1850年前后，乔治.布尔将逻辑值true和false编码成1和0，能够设计成一种代数，用来研究逻辑推理的原则。布尔代数就产生啦。

1.1.4C语言上的位级运算

C语言的一个很有用的特性就是支持按位进行布尔运算

C语言中的移位运算

左移：x向左移动k位，丢掉最高的k位，并在右端补k个零。

逻辑右移：在左端补k个零。

算数右移：在左端补k个最高位。

C语言并没有明确规定对有符号数使用那种类型的右移。但是编译器默认对有符号数使用算数右移，对无符号数使用逻辑右移。

1.2整数的表示

1.2.1C语言中的整数数据类型

C语言支持多种整数类型——表示有限范围的整数

 

1.2.2无符号数的编码

最大的无符号数B2U₄([1111]),最小的无符号数B2U₄([0000])

1.2.3补码编码

补码最高位是符号位，权重为-2^w-1，最高位为1时表示负数，为0时表示自然数。

TMin₄ = B2U₄([1000]) = -8,TMax₄ = B2U₄([0111]) = 7，因为零的存在，补码的最大值与最小值是不对称的。 

|TMin| = TMax+1，UMax(无符号最大值) = 2*TMax+1

原码、反码、补码

0和正整数的原码、反码、补码都一样。[+1] = [00000001]_原 = [00000001]_反 = [00000001]_补

负数：原码（符号位为1），反码（原码除符号位取反）、补码（反码+1）[-1] = [10000001]_原 = [11111110]_反 = [11111111]_补

1.2.4有符号数与无符号数的转化，位的扩展与截断

有符号和无符号转化：

1. 　　内存中每一个字节的值不会改变，改变的是计算机解释当前值得方式。
2. 　　如果一个表达式既包含有符号数也包含无符号数，有符号数会被隐式转化成无符号数。

类型扩展（保持原始数据的大小，扩充数据的位数）

1. 无符号数：加零
2. 有符号数：加符号位

类型截取（保持内存中的字节值不变）

1. 无符号与有符号数：mod操作（有符号数注意符号位的变化，可能会出现溢出）。

1.2.5整数运算

通过上面这几个函数我们看到了C语言是怎么处理溢出的。

char的范围为[-128~127]，b应该等于128，但是超出了char的范围。所以补码的非处理溢出会按照公式执行。

1.3浮点数表示

浮点数表示对形如V = x*2^y的有理数进行的编码。(0<<|V|<<1)。1976年在Intel的赞助下，在Kahan（加州大学的一位教授）作为顾问的帮助下，IEEE委员会终于于1985年完成了IEEE标准，并被所有的计算机支持。

1.3.1理解二进制小数

理解浮点数的第一步理解含有小数值的二进制数字，小数位的权重。

具体的浮点数的表示

浮点数转化为二进制数小数点前后也采取了不同的方式，小数点前除以2，小数点后乘以二，例如：4.75 = [100.11]

 1.3.2IEEE浮点表示

IEEE浮点标准用V = (-1)^s*M*2^E来表示一个数。

s=>符号位（sign），正数（s=0），负数（s=1）

M=>尾数（signficand），表示一个二进制小数，范围是1~2-€，或者是0~1-€

E=>阶数（exponent），作用对浮点数进行加权，这个权重是2的E次幂。

IEEE的浮点数表示分为三种情况（规格化数、非规格化数、特殊值）

规格化的值（当exp的二进制不全为零也不全为一时，按这种情况表示）

1. 阶码的值：E = e-Bias，e =无符号数的形式解析exp存储的二进制序列，Bias（固定值） = 2^阶数-1-1，可以看做是T_max。当e存储的序列较小时，E可能会取负值。
2. 尾数的值：M = 1+frac，规格化的数中规定尾数要以1开头，可能通过调整阶码使尾数固定以1开头，这样就不用显示的表示开头的1，可以节省一个位的存储并且提高浮点数精度。

非规格化的值（当exp的二进制全为零，具有两个用途）

1. 阶码值：E = 1-Bias， 尾数值：M = frac
2. 当frac全为0时，得到的值表示0，当s=0时是+0，当s=-1时表示-0。
3. 当frac为非零时，E = -126（单精度）或者-1022（双精度），所以非规格化数一般表示一种非常接近于零的数。

特殊值（当exp的二进制全为一，具有两个用途）

1. 当frac全为0时，得到的值表示无穷，当s=0时是+∞，当s=-1时表示-∞。
2. 当frac为非零时，结果值被称为“NAN”,表示“不是一个数”。

 1.3.3浮点数舍入

IEEE浮点格式定义了四种不同的舍入方式，默认的方法是找到向偶数舍入（最接近的匹配）。

向偶数舍入：试图找到一个最接近的匹配模式（14.舍入为1,1.6舍入为2）。唯一的设计决策（不存在最接近的舍入时，采取向偶数舍入）将数字向上或者向下舍入，使得结果的最低有效数字为偶数，例如1.5和2.5两个中间数都舍入为2。

向零舍入：正数向下舍入，负数向上舍入。