1D.小a与黄金街道（C++）

小a与黄金街道（C++）

点击做题网站链接

题目描述
小a和小b来到了一条布满了黄金的街道上。它们想要带几块黄金回去，然而这里的城管担心他们拿走的太多，于是要求小a和小b通过做一个游戏来决定最后得到的黄金的数量。
游戏规则是这样的：
假设道路长度为n米(左端点为0，右端点为n)，同时给出一个数k(下面会提到k的用法)
设小a初始时的黄金数量为A，小b初始时的黄金数量为B
小a从1出发走向n−1，小b从n−1出发走向1，两人的速度均为1m/s
假设某一时刻(必须为整数)小a的位置为x，小b的位置为y，若gcd(n,x)=1且gcd(n,y)=1，那么小a的黄金数量A会变为$A∗k^x(kg)$，小b的黄金数量B会变为$B∗k^y(kg)$
当小a到达n−1时游戏结束
小a想知道在游戏结束时A+B的值
答案对$10^9+7$取模

输入描述:
一行四个整数n,k,A,B

输出描述:
输出一个整数表示答案

示例1
输入
4 2 1 1

输出
32

说明
初始时A=1,B=1
第一个时刻如图所示，小a在1，小b在3，满足条件，此时
$A=1∗2^1=2,B=1∗2^3=8$

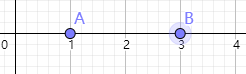
第二个时刻小a在2，小b在2，不满足条件

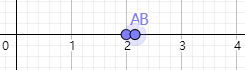
第三个时刻小a在3，小b在1，满足条件，此时
$A=2∗2^3=16,B=8∗2^1=16$

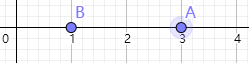
此时游戏结束
$A=2∗2^3=16,B=8∗2^1=16$
$A+B=32$

示例2
输入
5 1 1 1

输出
2

备注:
保证$3⩽n⩽10^8,1⩽A,B,k⩽10^13$

解题思路：

解题代码：

#include <iostream>
#include <cmath>
#define LL long long
using namespace std;
const LL mod=1e9+7;

LL ksm(LL a,LL b)//快速幂
{
    LL ans = 1;
    a %= mod;
    while( b>0 )
    {
        if( b&1 ) ans = (ans*a)%mod;
        b >>= 1;//位运算，右移1位，相当于除以2
        a = (a*a)%mod;
    }
    return ans;
}

LL Euler(LL n)//欧拉函数：求出小于等于n且与n互质的个数
{
    LL ans = n;
    for(int i=2;i<=sqrt(n);++i)
    {
        if( n%i==0 ) 
        {
            ans -= ans/i;
            while( n%i==0 )
                n /= i;
        }
    }
    if( n>1 ) return ans -= ans/n;
    return ans;
}

int main() 
{
    ios::sync_with_stdio(false);
    LL n, k, A, B;
    cin >> n >> k >> A >> B;
    cout << ( (A+B)*ksm(k,Euler(n)/2*n) ) % mod << endl;
}