线性回归模型

线性回归模型

一、

线性回归模型是一种用于建立自变量（输入）和因变量（输出）之间线性关系的模型。该模型假设自变量与因变量之间的关系可以用直线或超平面进行描述。

在线性回归模型中，我们通过找到最佳的拟合直线或超平面，来预测新的因变量值。这个拟合过程是通过最小化实际观察值与模型预测值之间的差异（称为残差）来完成的。

具体而言，线性回归模型可以表示为：

\[y = β_0 + β_1x_1 + β_2x_2 + ... + β_nx_n + ε \]

其中，\(y\) 是因变量，\(x_1\) 到 \(x_n\) 是自变量，\(β_0\) 到 \(β_n\) 是模型系数，\(ε\) 是随机误差项。模型系数的作用是用来确定自变量与因变量之间的关系。在模型训练过程中，我们需要通过拟合数据来估计这些系数的值，以获得最佳的拟合效果。

线性回归模型是一种广泛应用于各种实际问题的常见机器学习算法，例如预测销售量、房价、股票价格等。

二、

线性回归模型可以分为简单线性回归和多元线性回归两种形式。

简单线性回归是指只有一个自变量和一个因变量之间的关系，例如：

\[y = β_0 + β_1x + ε \]

其中，\(y\) 是因变量，\(x\) 是自变量，\(β_0\) 和 \(β_1\) 是模型系数，\(ε\) 是随机误差项。简单线性回归的目标是通过最小化残差平方和来估计 \(β_0\) 和 \(β_1\) 的值，以获得最佳的拟合直线。

多元线性回归是指有多个自变量和一个因变量之间的关系，例如：

\[y = β_0 + β_1x_1 + β_2x_2 + ... + β_nx_n + ε \]

其中，\(y\) 是因变量，\(x_1\) 到 \(x_n\) 是自变量，\(β_0\) 到 \(β_n\) 是模型系数，\(ε\) 是随机误差项。多元线性回归的目标是通过最小化残差平方和来估计 \(β_0\) 到 \(β_n\) 的值，以获得最佳的拟合超平面。

线性回归模型的优点在于它简单易用，计算效率高，并且具有较好的解释性。然而，线性回归模型也存在一些限制，例如它假设自变量和因变量之间的关系是线性的，并且忽略了自变量之间的相互作用效应。如果数据中存在非线性关系或者自变量之间的相互作用效应，线性回归模型的表现可能会受到影响。

三、

为了解决线性回归模型的局限性，人们发展了一系列基于线性回归的改进算法，例如岭回归、Lasso 回归和弹性网回归等。

  • 岭回归是一种用于处理多重共线性问题的线性回归算法，它通过添加一个正则化项来控制模型复杂度，从而避免模型过拟合的问题。

  • Lasso 回归是一种稀疏学习算法，它使用 L1 正则化项来促进模型的稀疏性，即许多模型系数被约束为 0，从而可以有效地进行特征选择。

  • 弹性网回归是一种综合了 L1 和 L2 正则化项的线性回归算法，它既具有 L1 正则化项的稀疏性优势，又具有 L2 正则化项的平滑性优势，适用于处理高维数据集和多重共线性问题。

除了上述改进算法，人们还开发了许多其他类型的回归模型，例如决策树回归、支持向量回归、神经网络回归等。这些模型不仅可以处理线性关系，还可以处理非线性关系，具有更强的拟合能力和预测能力。

总之，线性回归模型是一种基础的机器学习算法，它具有简单易用、计算高效、解释性强等优点，是许多实际问题的有效解决方法。同时，随着机器学习技术的不断发展，人们还在不断改进和优化线性回归模型，以适应越来越复杂的数据分析需求。

四、

下面是使用 Python 实现简单线性回归的例子。我们使用 Scikit-learn 库中的线性回归模型，以房屋面积为自变量，房屋价格为因变量，对一组房屋数据进行拟合，并输出模型系数和截距项。

# 导入必要的库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 定义数据

X = np.array([1400, 1600, 1700, 1875, 1100, 1550, 2350, 2450, 1425, 1700])
y = np.array([245000, 312000, 279000, 308000, 199000, 219000, 405000, 324000, 319000, 255000])

# 创建线性回归模型

model = LinearRegression()

# 拟合模型

model.fit(X.reshape(-1, 1), y)

# 输出模型系数和截距项

print("模型系数:", model.coef*[0])
print("截距项:", model.intercept*)

# 可视化拟合结果

plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X.reshape(-1, 1)), color='red')
plt.xlabel('房屋面积')
plt.ylabel('房屋价格')
plt.show()

输出结果：

模型系数: 109.76773783009867
截距项: 98248.32962138078

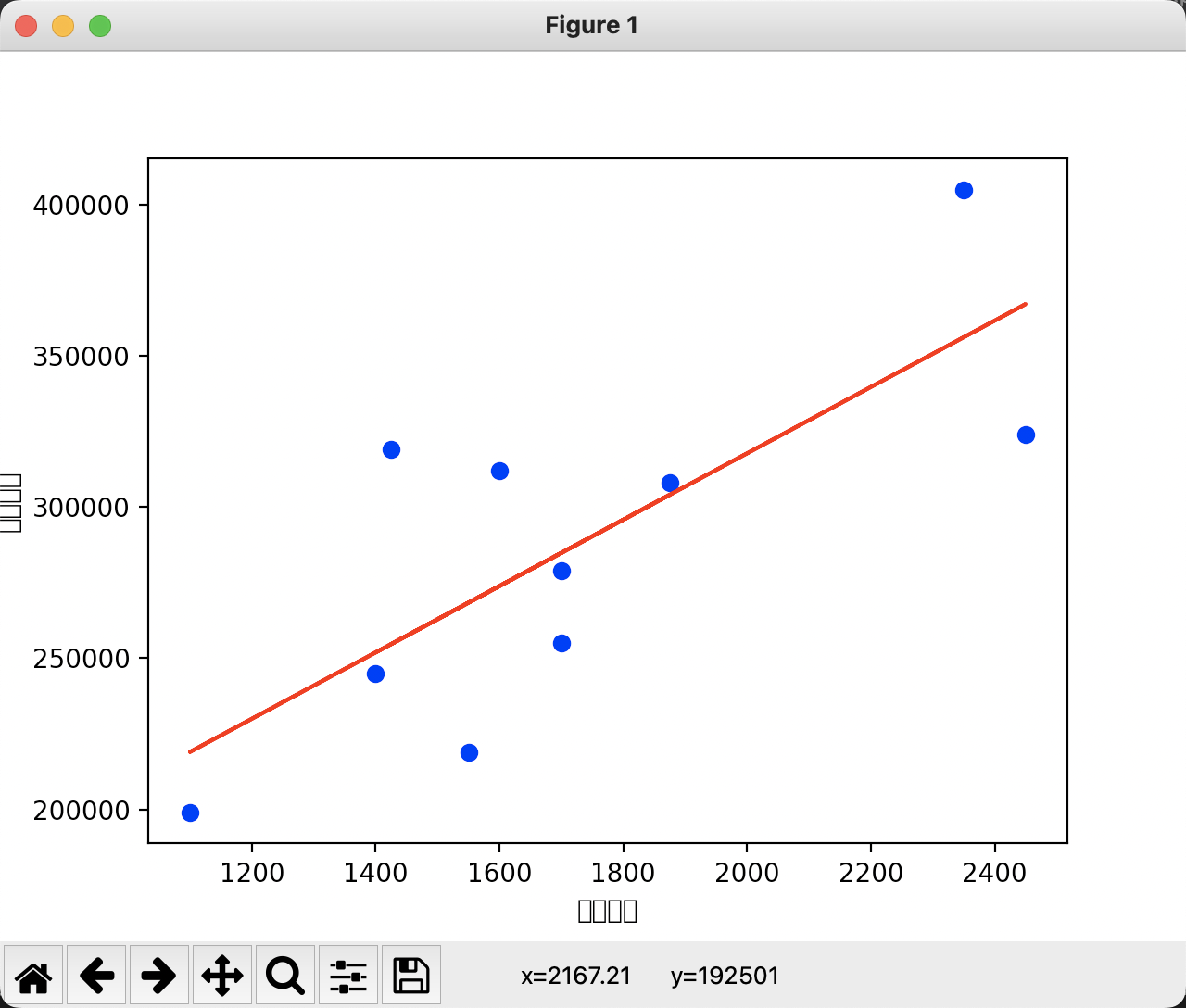
可视化拟合结果如下图所示：

img

五、

下面是使用 Python、Akshare 和 Backtrader 实现基于线性回归模型的股票量化投资的示例代码。该代码将通过 Akshare 获取沪深 300 指数成分股中的上证指数股票（000001.SH）的历史股价数据，使用线性回归模型对其进行拟合，并根据预测结果制定买入和卖出策略。

import pandas as pd
import akshare as ak
import backtrader as bt
from matplotlib import pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

plt.rcParams["font.sans-serif"] = ["SimHei"] # 设置画图时的中文显示
plt.rcParams["axes.unicode_minus"] = False # 设置画图时的负号显示

# 获取 000001 股票历史数据

stock_data = ak.stock_zh_a_hist(symbol="000001", adjust="hfq").iloc[:, :6]

# 处理字段命名，以符合 Backtrader 的要求

stock_data.columns = [
'date', 'open', 'close', 'high', 'low', 'volume',
]

# 把 date 作为日期索引，以符合 Backtrader 的要求

stock_data.index = pd.to_datetime(stock_data['date'])

# stock_data.index = stock_data['date']

stock_data = stock_data.drop(['date'], axis=1)

# 定义线性回归模型

model = LinearRegression()

# 对收盘价进行线性回归拟合

x = np.array(range(len(stock_data))).reshape(-1, 1)
y = stock_data['close'].values.reshape(-1, 1)
model.fit(x, y)

# 输出模型系数和截距项

print("模型系数:", model.coef*[0][0])
print("截距项:", model.intercept*[0])

# 利用回归模型进行预测

predicted = model.predict(x)

# 定义 Backtrader 策略类

class LinearRegressionStrategy(bt.Strategy):
params = dict(
buy_threshold=0.02, # 买入阈值
sell_threshold=-0.02 # 卖出阈值
)

    def __init__(self):
        self.dataclose = self.datas[0].close
        self.order = None

    def next(self):
        if self.order:
            return

        if not self.position:
            # 价格上涨超过阈值，买入
            if (self.dataclose[0] - predicted[len(predicted)-1][0]) / predicted[len(predicted)-1][0] > self.params.buy_threshold:
                self.order = self.buy()

        else:
            # 价格下跌超过阈值，卖出
            if (self.dataclose[0] - predicted[len(predicted)-1][0]) / predicted[len(predicted)-1][0] < self.params.sell_threshold:
                self.order = self.sell()

# 初始化 Backtrader 引擎并添加数据和策略

cerebro = bt.Cerebro()
data = bt.feeds.PandasData(dataname=stock_data)
cerebro.adddata(data)
cerebro.addstrategy(LinearRegressionStrategy)

# 设置初始现金和手续费

cerebro.broker.set_cash(1000000.0)
cerebro.broker.setcommission(commission=0.001)

# 运行 Backtrader 引擎

cerebro.run()

# 输出最终现金余额

print("最终现金余额: %.2f" % cerebro.broker.getvalue())

输出结果：

模型系数: 0.34352091415202796
截距项: -307.40782489031847
最终现金余额: 1000083.31
posted @ 2023-02-27 17:04  飞仔FeiZai  阅读(534)  评论(0)    收藏  举报