第二章 算法分析

2.1 算法分析

• 算法就是解决问题的方法。
• 程序就是采用某种编程语言实现对算法的编程。
• 同一个算法可以对应许多程序，这取决于程序员和编程语言。

例2.1 计算前n个整数之和（暴力解法）

def sumofN(n):
    sumN=0
    for i in range(1,n+1):
        sumN+=i
    return sumN
print(sumofN(10))

例2.2 计算前n个整数之和（计算执行时间）

• time模块中有一个time函数，它会以秒为单位返回自指定时间点起到当前的系统时钟时间。在首尾各调用一次这个函数，计算差值，就可以得到以秒为单位的执行时间。

import time
def sumofN(n):
    sumN=0
    start=time.time()
    for i in range(1,n+1):
        sumN+=i
    end=time.time()
    return sumN,end-start
print("Sum of N is %d and required %10.7f seconds" % sumofN(100000000))

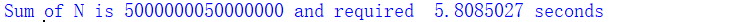
例2.3 计算前n个整数之和（公式法）

• 求和公式n*(n+1)/2

import time 
def sumofN(n):
    start=time.time()
    sumN=(n*(n+1))/2
    end=time.time()
    return  sumN, start-end
print("Sum of N is %d and required %10.7f seconds" % sumofN(100000000))

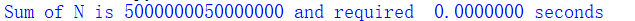
计算资源究竟是什么？

• 一是考虑算法在解决问题时要占用的空间和内存。空间总量一般由问题实例本身决定，但算法往往会有特定的空间需求。
• 二是根据算法执行所需的时间进行分析和比较，即执行时间或运行时间。基准测试计算的都是执行算法的实际时间。

2.1.1 大O计法

• T（n）=所有操作的步数的总和，n表示问题的规模
• 算法的执行时间随问题规模而变化
• 数量级常被称作为大O记法（O指的order）,记作O（f(n)）
  • f(n)函数为T（n）函数中起决定性作用的部分提供了简单的描述。
  • 数量级表示是指当n增长时，增长最快的部分作为T（n）的决定性部分。
  • eg.T（n）=1+n,随着n越来越大，常数1对最终结果的影响越来越小，给出T（n）的近似值为，可以舍去1，那么执行时间为O（n）
• 算法的性能有时不仅依赖于问题规模，还依赖于数据值，要用最坏情况、最好情况和普通情况来描述性能。
  • 最坏情况是指某一个数据集会让算法的性能极差
  • 最好情况是指某一个数据集会让算法的性能极好
  • 普通情况是算法的性能介于两个极端之间。
• 常见的大O函数
  

2.1.2 异序词检测示例

• 概念：如果一个字符串只是重排了另一个字符串的字符，那么这个字符串就是另一个的异序词
• 目标：编写一个布尔函数，它接受两个字符串，并能判断它们是否为异序词

例2.4 清点法

• 思路：清点是通过用Python中的特殊值None取代字符来实现的，但是字符串是不可修改的，先将第2个字符串转换为列表，在字符列表中检查第1个字符串中的每个字符，如果找到了，就替换掉。

def solution(s1,s2):
    ls1=list(s1)
    ls2=list(s2)
    for i in ls1:
        for j in range(len(ls2)):
            if ls2[j]==i:
                ls2[j]=None
    s=0
    for i in ls2:
        if i ==None:
            s+=1

    if s==len(ls2):
        return True

if solution('lst','slt'):
    print("两个字符串为异序数")
else:
    print("两个字符串不是异序数")

• 列表中的n个位置都要被访问一次，因此访问次数为n^2+n,那么时间复杂度就为O（n^2）

例2.5 排序法

• 思路：可以先将字符串转换为列表，然后使用内建的sort方法对列表排序

def solution(s1,s2):
    ls1=list(s1)
    ls2=list(s2)
    ls1.sort()
    ls2.sort()
    if ls1==ls2:
        return True
if solution('lst','slt'):
    print("两个字符串为异序数")
else:
    print("两个字符串不是异序数")

• 该算法的时间复杂度应为O（1）

2.2 python数据结构的性能

2.2.1 列表

• 操作以及对应的时间复杂度
  • 索引：常数阶，与列表长度无关
  • 给某个位置赋值：常数阶，与列表长度无关
  • 加长列表:
    • 追加：常数阶
    • 执行连接操作：O（k）,k是连续列表的长度

例2.6 生成列表的4种方式

• timeit模块：
  • 使用该模块创建Timer对象，第一个参数是计时的方法，第二个参数是建立测试的语句

from timeit import Timer
def test1(): #通过for循环连接创建列表
    l1=[]
    for i in range(1000):
        l1=l1+[i]
def test2(): #通过追加的方式
    l2=[]
    for i in range(1000):
        l2.append(i)
def test3():#列表解析式
    l3=[]
    l3=[i for i in range(1000)]
def test4():#列表构造器调用range
    l4=list(range(1000))
# Press the green button in the gutter to run the script.
if __name__ == '__main__':

    t1=Timer("test1()","from __main__ import test1")
    print("concat",t1.timeit(number=1000),"milliseconds")#运行1000次

    t2=Timer("test2()","from __main__ import test2")
    print("append",t2.timeit(number=1000),"milliseconds")#运行1000次

    t3=Timer("test3()","from __main__ import test3")
    print("comprehension",t3.timeit(number=1000),"milliseconds")#运行1000次

    t4=Timer("test4()","from __main__ import test4")
    print("list range",t4.timeit(number=1000),"milliseconds")#运行1000次

• 最后一种赋值方法最快

• 各个操作的时间复杂度
  

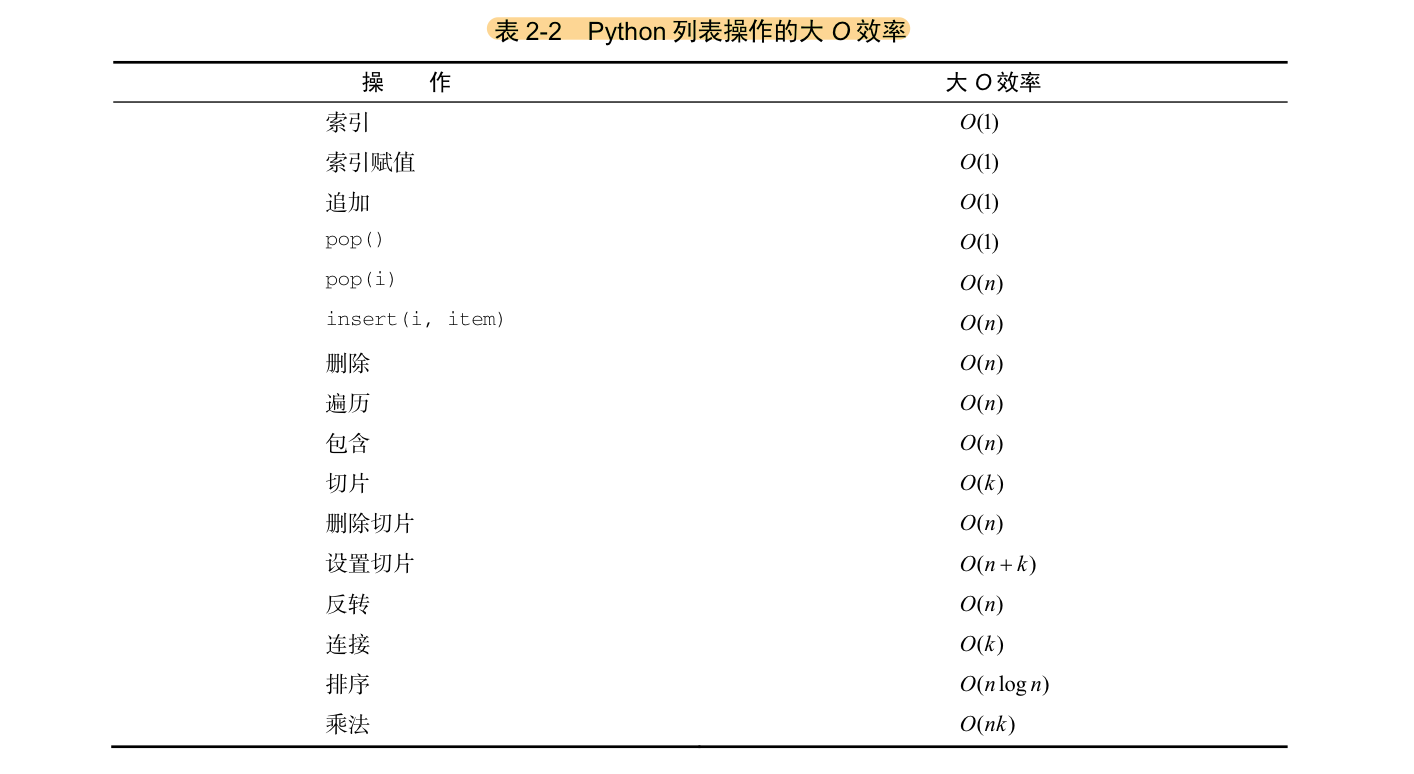
2.2.2 字典

• 操作及对应的时间复杂度

• 列表的包含操作是O（n）,字典的包含操作是O（1），包含操作就是判断元素是否在。