动手学深度学习v2-07-1自动求导

自动求导

• 深度学习框架通过自动计算导数，即自动求导（automatic differentiation），来加快这项工作。
• 根据我们设计的模型，系统会构建一个计算图，来跟踪计算是哪些数据通过哪些操作组合起来产生输出。
• 自动求导使系统能够随后反向传播梯度
• 反向传播只是意味着跟踪整个计算图，填充关于每个参数的偏导数。

1 向量链式法则

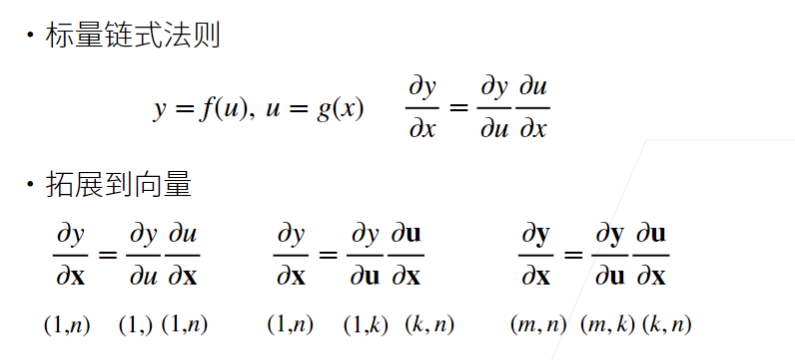
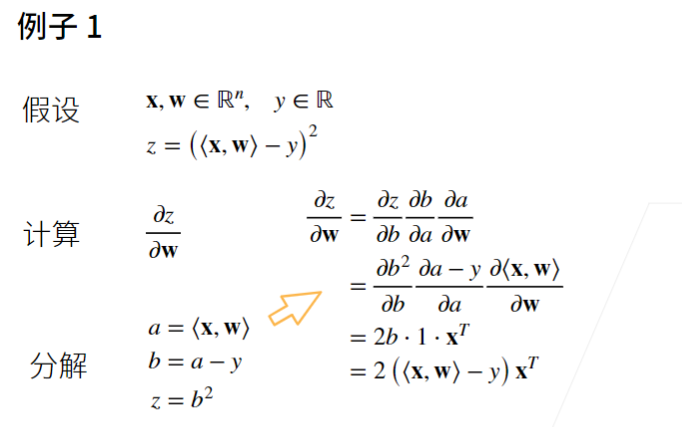
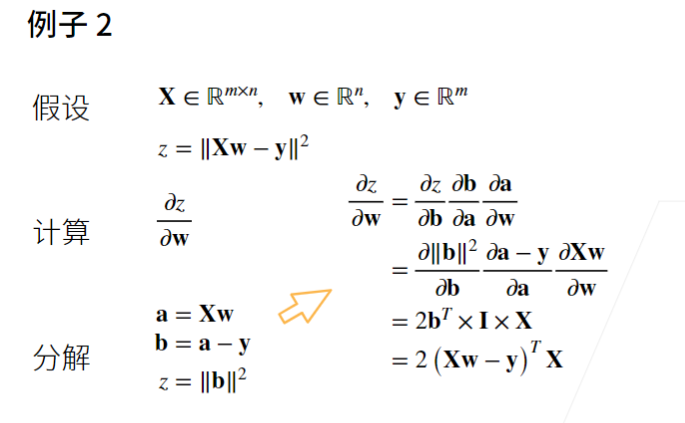
2 自动求导

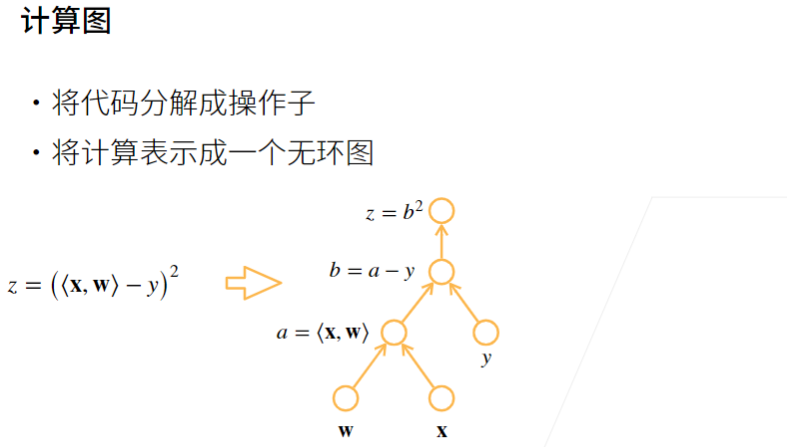
2.1 自动求导的两种模式

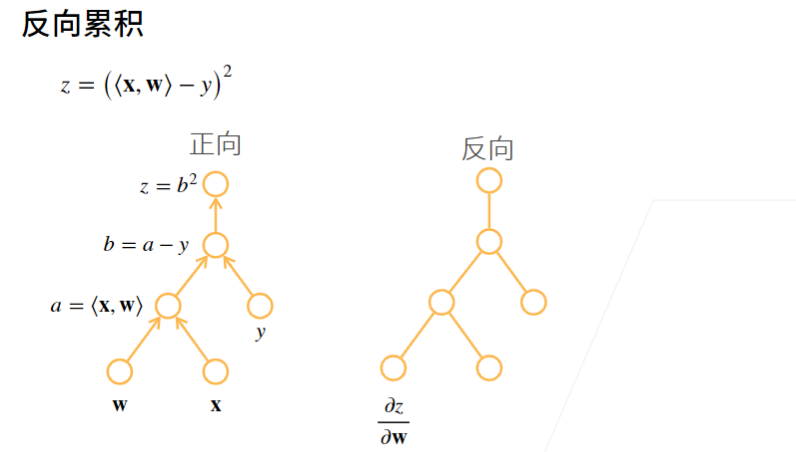
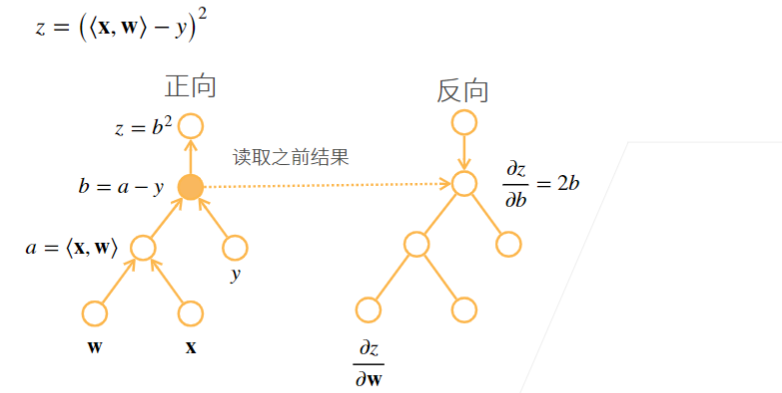
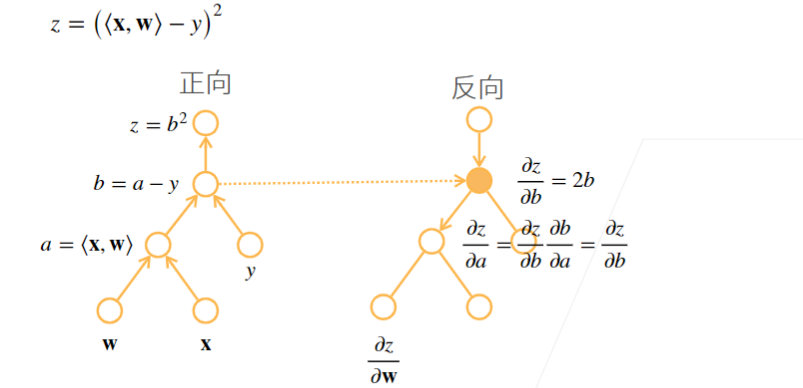
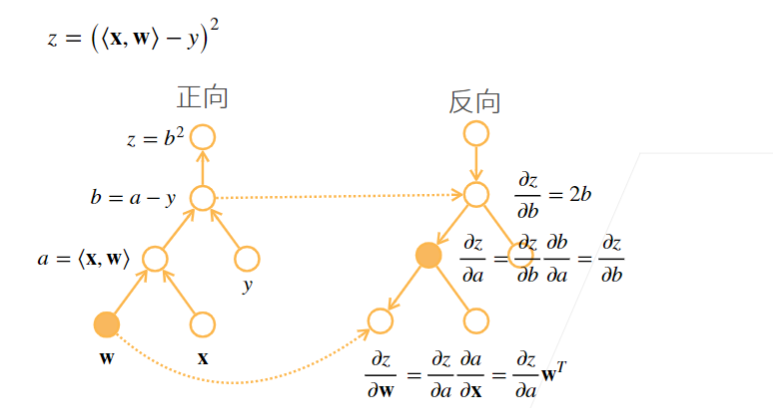
2.2 例子

• 创建变量x并为其分配一个初始值

import torch

x = torch.arange(4.0)
x

• x.grad来存储梯度

标量函数关于向量 x 的梯度是向量，并且与 x 具有相同的形状。

x.requires_grad_(True)  # 等价于 `x = torch.arange(4.0, requires_grad=True)`
x.grad  # 默认值是None

• 计算Y值

y = 2 * torch.dot(x, x)
y

• 调用反向传播函数来自动计算y关于x每个分量的梯度，并打印这些梯度。

x是一个长度为4的向量

y.backward()
x.grad

• 我们知道关于x的梯度为4x,我们想要验证梯度是否正确。

x.grad == 4 * x

2.3 非标量变量的反向传播

• 计算批量中每个样本单独计算的偏导数之和

# 对非标量调用`backward`需要传入一个`gradient`参数，该参数指定微分函数关于`self`的梯度。在我们的例子中，我们只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad

2.4 分离计算

• 我们可以分离y来返回一个新变量u，该变量与y具有相同的值，但丢弃计算图中如何计算y的任何信息。

下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理，而不是z=x * x * x关于x的偏导数。

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u

2.5 Python控制流的梯度计算

使用自动求导的一个好处是，即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度。

下面的代码中，while循环的迭代次数和if语句的结果都取决于输入a的值

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

• 计算梯度

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()

• 验证梯度是否正确

a.grad == d / a

3 小结

我们首先将梯度附加到想要对其计算偏导数的变量上。然后我们记录目标值的计算，执行它的反向传播函数，并访问得到的梯度。