动手学机器学习v2-05-1线性代数
线性代数
1 标量

- 标量由只有一个元素的张量表示。
# 标量的基本运算
import torch
x=torch.tensor([3.0])
y=torch.tensor([2.0])
x+y,x*y,x/y,x**y

2 向量

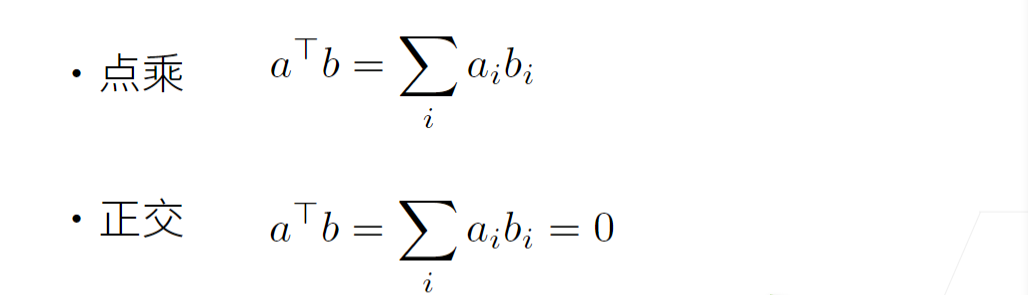
-
将向量视为标量值组成的列表
-
将这些标量值称为向量的元素(element)或分量(component)
-
创建向量
x = torch.arange(4)
x

- 通过张量的索引来访问任一元素
x[3]

- 向量的长度
len(x)

x.shape

3 矩阵
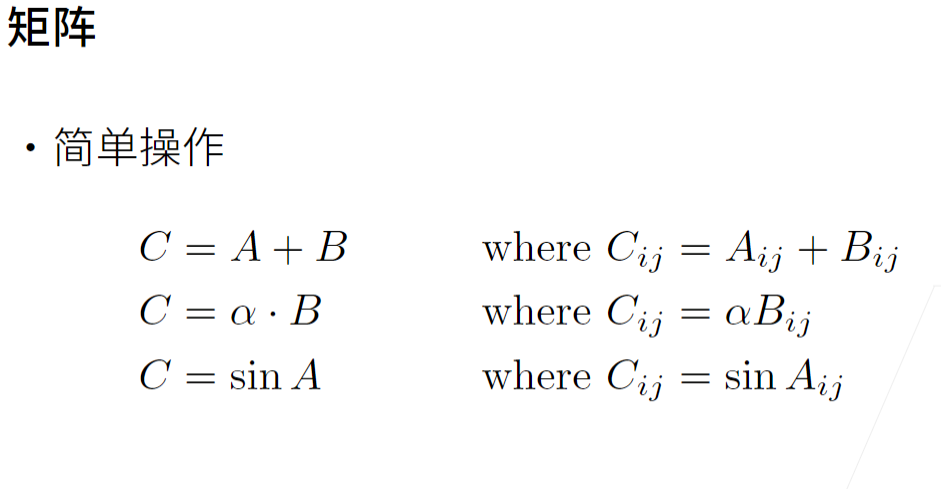

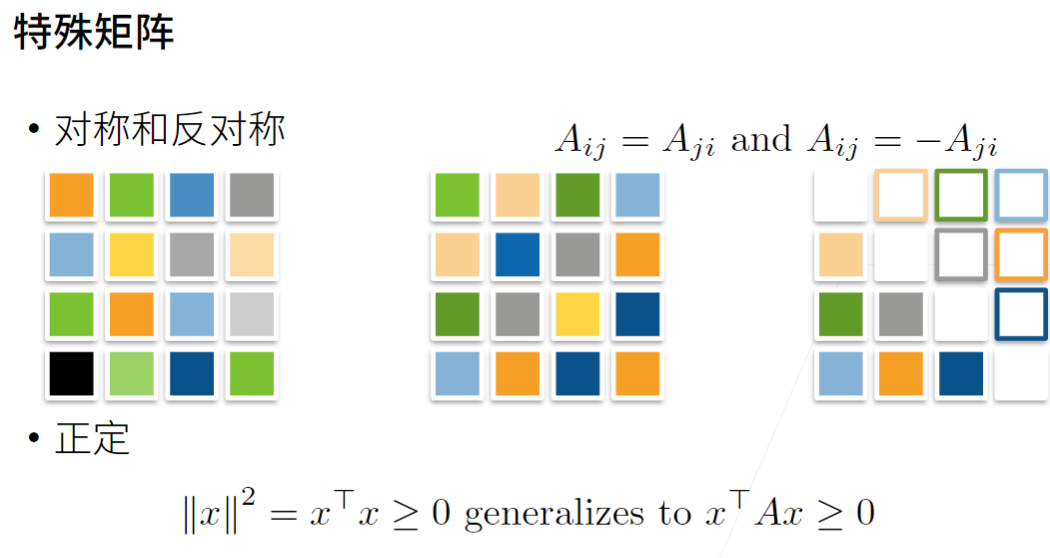

- 调用函数来实例化张量时,指定两个分量m和n来创建一个形状为m*n的矩阵
A = torch.arange(20).reshape(5, 4)
A

- 矩阵的转置
A.T

- 对称矩阵
# 定义一个对称矩阵
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B

# 将B与B.T进行对比
B == B.T

4 张量
4.1 张量的定义
-
张量为我们提供了描述具有任意数量轴的 n 维数组的通用方法。例如,向量是一阶张量,矩阵是二阶张量。
-
处理图像时,张量将变得更加重要,图像以 n 维数组形式出现,其中3个轴对应于高度、宽度,以及一个通道(channel)轴,用于堆叠颜色通道(红色、绿色和蓝色)
-
创建三维张量
X = torch.arange(24).reshape(2, 3, 4)
X

4.2 张量的基本性质
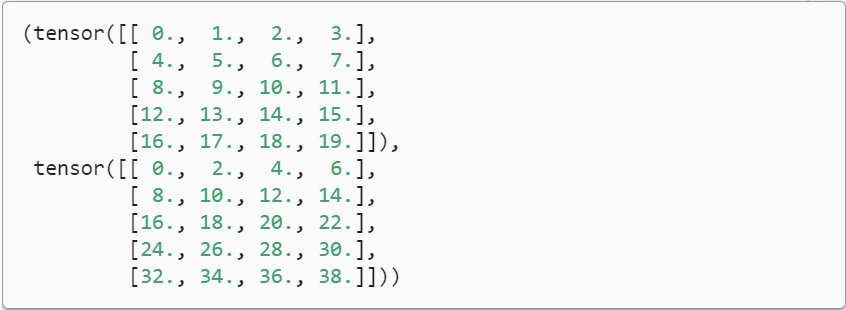
- 将两个相同形状的矩阵相加会在这两个矩阵上执行元素加法
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A + B
- 矩阵 A 和 B 的哈达玛积为:
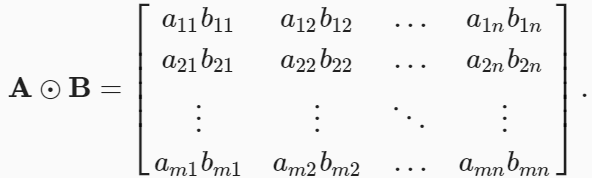
A * B
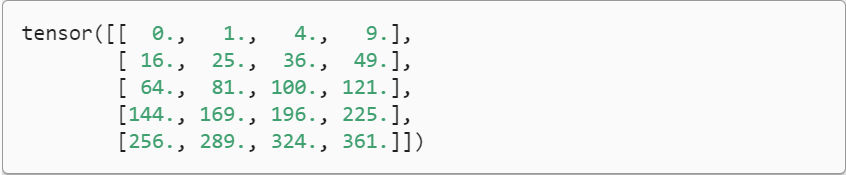
- 将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

4.3 张量的降维
-
本质就是某个维度进行求和,从而消除这个维度
-
简单的向量(一阶张量)求和
x = torch.arange(4, dtype=torch.float32)
x, x.sum()

- 任意形状张量的元素和
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A.shape, A.sum()

- 默认情况下,调用求和函数会沿所有的轴降低张量的维度
以矩阵为例,为了通过求和所有行的元素来降维(轴0),我们可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量,因此输入的轴0(行)的维数在输出形状中丢失
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

# 指定axis=1将通过汇总所有列的元素降维(轴1)。因此,输入的轴1的维数在输出形状中消失。
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

# 沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和
A.sum(axis=[0, 1]) # Same as `A.sum()`

- 调用函数来计算任意形状张量的平均值
A.mean(), A.sum() / A.numel()

- 计算平均值的函数也可以沿指定轴降低张量的维度
A.mean(axis=0), A.sum(axis=0) / A.shape[0]

- 调用函数来计算总和或均值时保持轴数不变(非降维求和)会很有用
sum_A = A.sum(axis=1, keepdims=True)
sum_A

- 调用cumsum函数,某个轴计算A元素的累积总和
此函数不会沿任何轴降低输入张量的维度
A.cumsum(axis=0)

5 点积的运算
- 点积<x,y>是相同位置的按元素乘积的和:
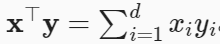
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

- 我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积
torch.sum(x * y)

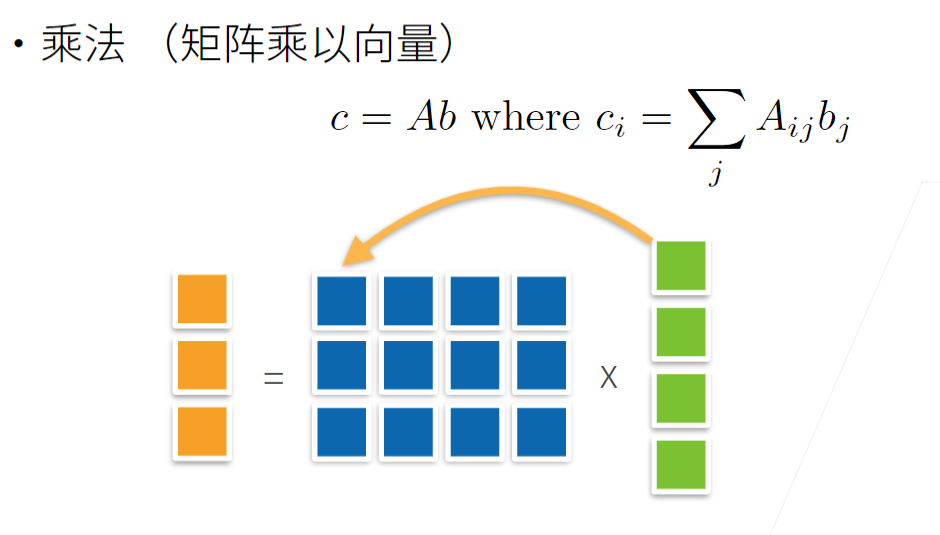
6 矩阵-向量积
- 当我们为矩阵A和向量x调用np.dot(A,x)时,会执行矩阵-向量积。
注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
A.shape, x.shape, torch.mv(A, x)

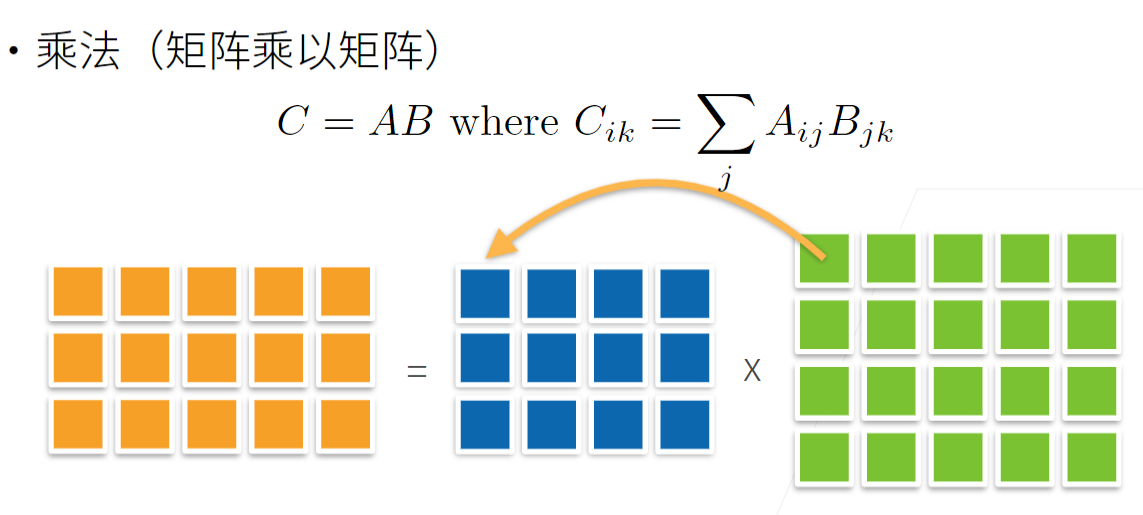
7 矩阵-矩阵乘法

B = torch.ones(4, 3)
torch.mm(A, B)

8 范数
- L2 范数是向量元素平方和的平方根
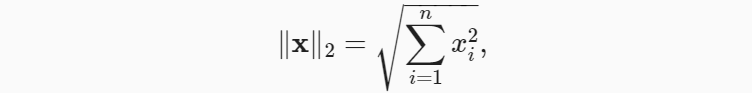
u = torch.tensor([3.0, -4.0])
torch.norm(u)

- L1 范数为向量元素的绝对值之和
与 L2 范数相比, L1 范数受异常值的影响较小
torch.abs(u).sum()

- 弗罗贝尼乌斯范数(Frobenius norm)是矩阵元素平方和的平方根:
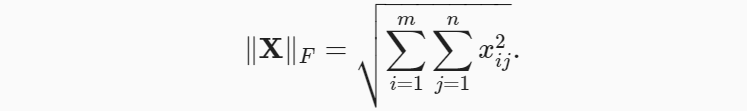
torch.norm(torch.ones((4, 9)))


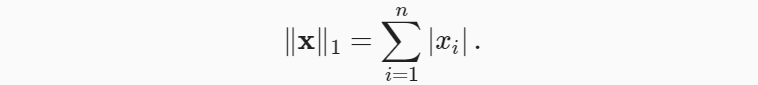

 浙公网安备 33010602011771号
浙公网安备 33010602011771号