决策树算法2-决策树分类原理2.1-信息熵
熵
1 概念
1.1 起源
- 物理学上,熵 Entropy是“混乱”程度的量度。系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
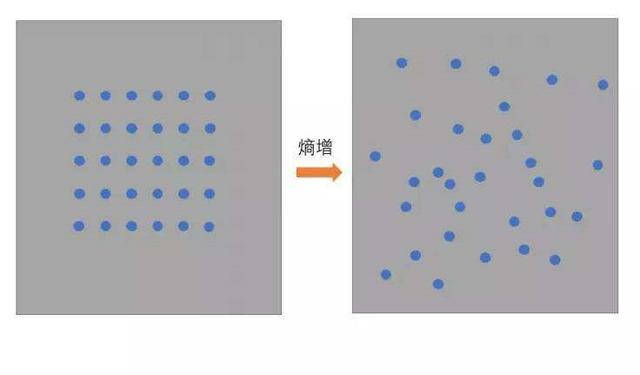
- 1948年香农提出了信息熵(Entropy)的概念。
1.2 信息理论
- 从信息的完整性上描述:系统的有序状态一致时,数据越集中的地方熵值越小,数据越分散的地方熵值越大。
- 从信息的有序性上描述:数据量一致时,系统越有序,熵值越低;系统越混乱或者分散,熵值越高。
1.3 信息熵定义
- "信息熵" (information entropy)是度量样本集合纯度最常用的一种指标。
- 假定当前样本集合 D 中第 k 类样本所占的比例为\(p_k(k = 1, 2,. . . , |y|), p_k=\frac{c_k}{D}\), D为样本的所有数量,\(c_k\)为第k类样本的数量。则D的信息熵定义为(log是以2为底,lg是以10为底):
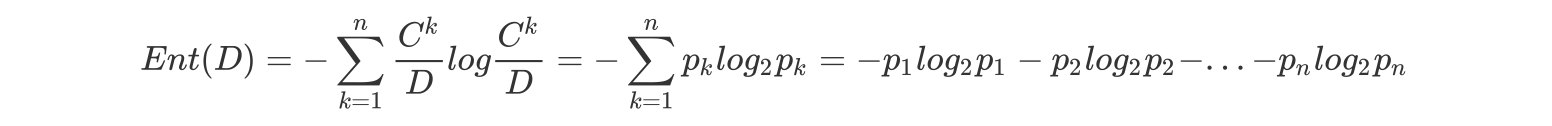
其中:Ent(D) 的值越小,则 D 的纯度越高.
2 案例
课堂案例:
假设我们没有看世界杯的比赛,但是想知道哪支球队会是冠军,
我们只能猜测某支球队是或不是冠军,然后观众用对或不对来回答,
我们想要猜测次数尽可能少,你会用什么方法?
答案:
二分法:
假如有 16 支球队,分别编号,先问是否在 1-8 之间,如果是就继续问是否在 1-4 之间,
以此类推,直到最后判断出冠军球队是哪支。
如果球队数量是 16,我们需要问 4 次来得到最后的答案。那么世界冠军这条消息的信息熵就是 4。
那么信息熵等于4,是如何进行计算的呢?
Ent(D) = -(p1 * logp1 + p2 * logp2 + ... + p16 * logp16),
其中 p1, ..., p16 分别是这 16 支球队夺冠的概率。
当每支球队夺冠概率相等都是 1/16 的时:Ent(D) = -(16 * 1/16 * log1/16) = 4
每个事件概率相同时,熵最大,这件事越不确定。
练习:
篮球比赛里,有4个球队 {A,B,C,D} ,获胜概率分别为{1/2, 1/4, 1/8, 1/8}
求Ent(D)
答案:
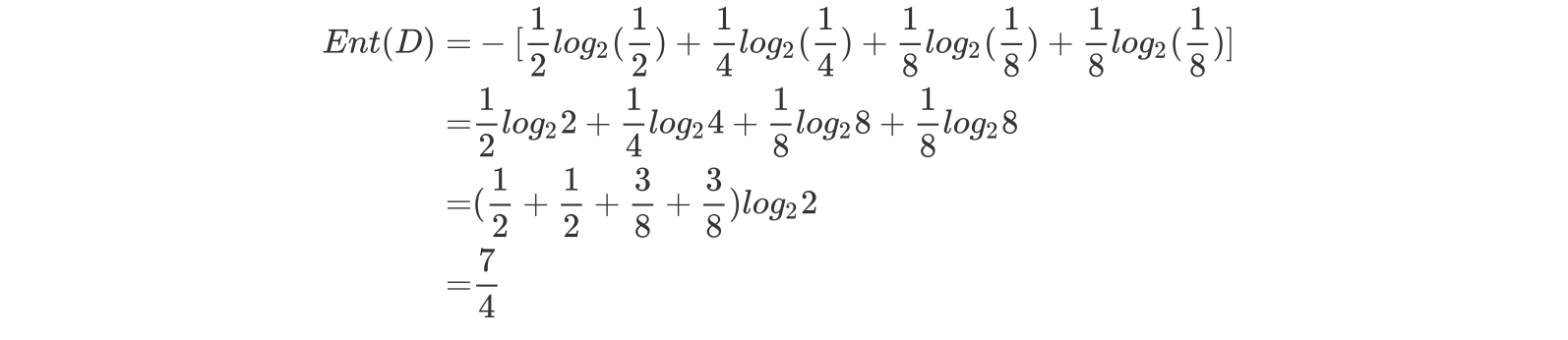


 浙公网安备 33010602011771号
浙公网安备 33010602011771号