线性回归4-梯度下降法介绍

1 全梯度下降算法（FG）

• 计算训练集所有样本误差，对其求和再取平均值作为目标函数。
• 在执行每次更新时，我们需要在整个数据集上计算所有的梯度，所以批梯度下降法的速度会很慢，同时，批梯度下降法无法处理超出内存容量限制的数据集。
• 批梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。
• 其是在整个训练数据集上计算损失函数关于参数θ的梯度：
  

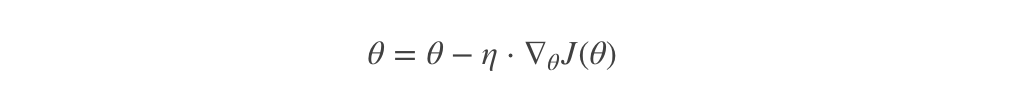
2 随机梯度下降算法（SG）

• 每次只代入计算一个样本目标函数的梯度来更新权重，再取下一个样本重复此过程，直到损失函数值停止下降或损失函数值小于某个可以容忍的阈值。
• 此过程简单，高效，通常可以较好地避免更新迭代收敛到局部最优解。其迭代形式为
  

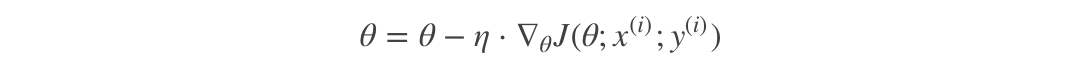
• 注：SG每次只使用一个样本迭代，若遇上噪声则容易陷入局部最优解。

3 小批量梯度下降算法（Mini-batch）

• 每次从训练样本集上随机抽取一个小样本集，在抽出来的小样本集上采用FG迭代更新权重。
• 小批量梯度下降算法是FG和SG的折中方案,在一定程度上兼顾了以上两种方法的优点。
• 被抽出的小样本集所含样本点的个数称为batch_size，通常设置为2的幂次方，更有利于GPU加速处理。
• 特别的，若batch_size=1，则变成了SG；若batch_size=n，则变成了FG.其迭代形式为
  

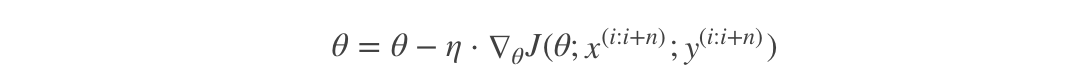
4 随机平均梯度下降算法（SAG）

• 在SG方法中，虽然避开了运算成本大的问题，但对于大数据训练而言，SG效果常不尽如人意，因为每一轮梯度更新都完全与上一轮的数据和梯度无关。
• 随机平均梯度算法克服了这个问题，在内存中为每一个样本都维护一个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，后期计算的时候，参考这个平均值，进而更新参数。
• 每一轮更新仅需计算一个样本的梯度，计算成本等同于SG，但收敛速度快得多。