线性回归3-线性回归的损失和优化

1 损失函数

总损失定义为：

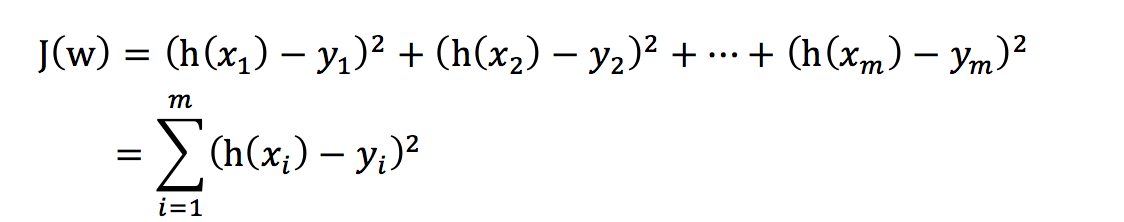
• yi为第i个训练样本的真实值
• h(xi)为第i个训练样本特征值组合预测函数
• 又称最小二乘法

我们想使得损失函数的值最小，就要通过一些优化方法去优化(即为数学当中的求导功能)回归的总损失。

2 优化算法

• 求模型当中的W，使得损失最小（找到最小损失对应的W值）
• 线性回归经常使用的两种优化算法
  • 正规方程
  • 梯度下降法

2.1 正规方程

2.1.1 什么是正规方程

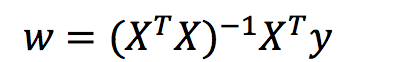
理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果
缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

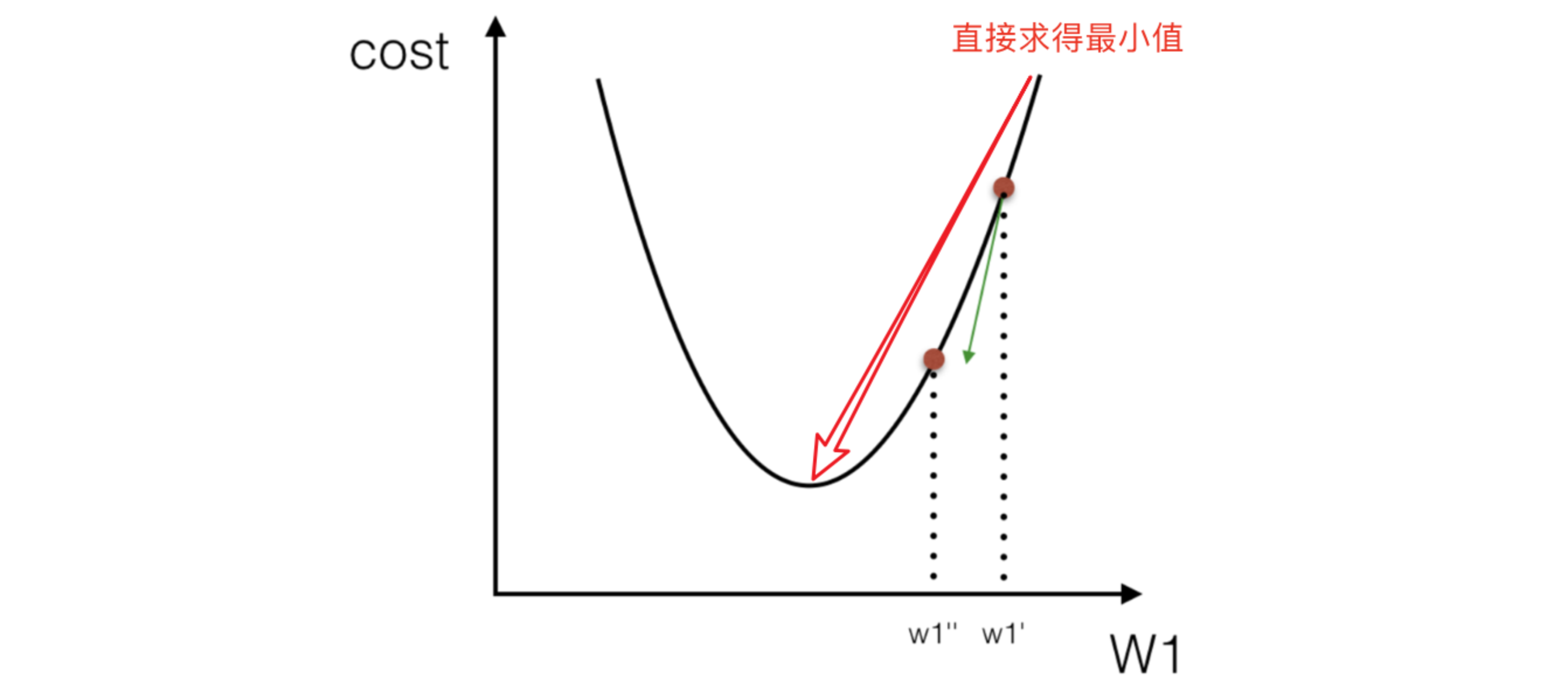
2.1.2 正规方程求解举例

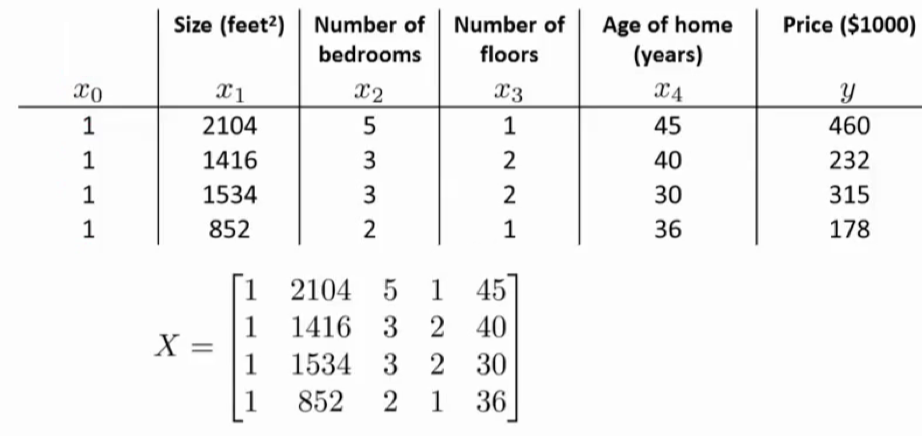
转化后的结果为：

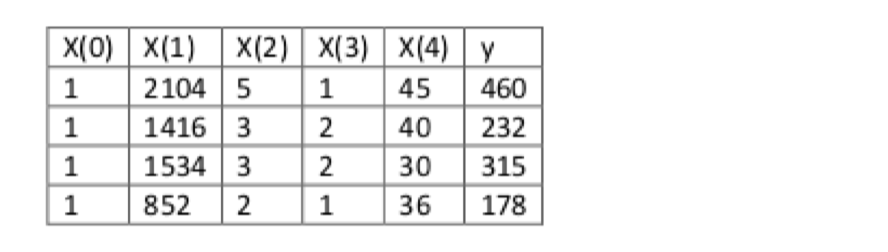
运用正规方程方法求解参数：

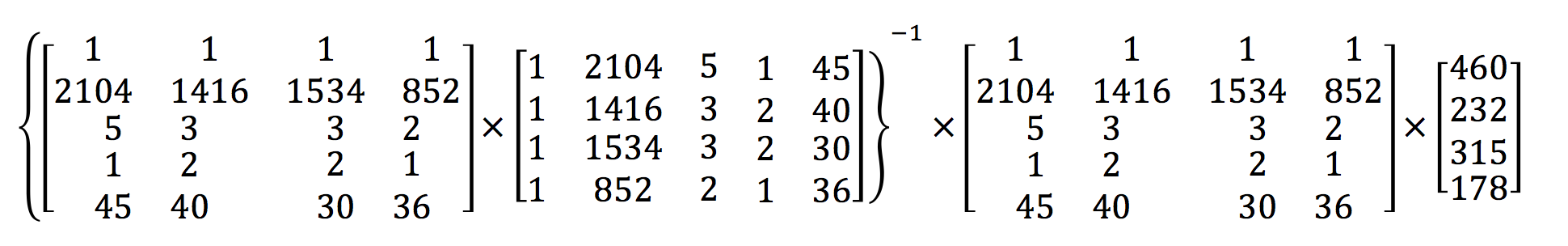
2.1.3 正规方程的推导

• 推导方式：
  把该损失函数转换成矩阵写法：

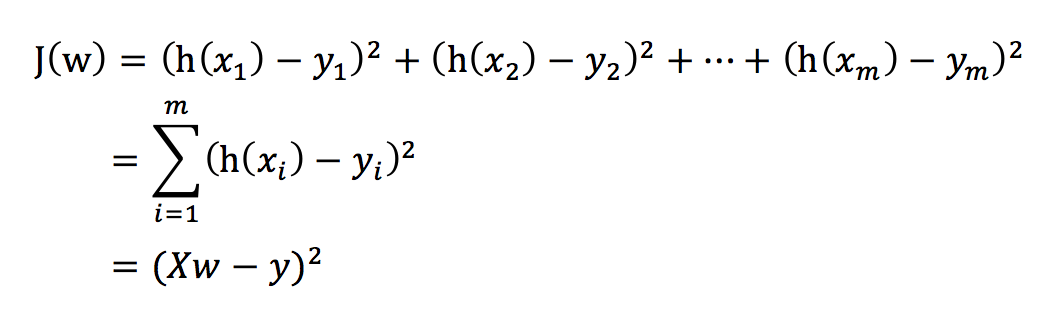
其中y是真实值矩阵，X是特征值矩阵，w是权重矩阵

• 求解思路：对其求解关于w的最小值，起止y,X 均已知二次函数直接求导，导数为零的位置，即为最小值。
  

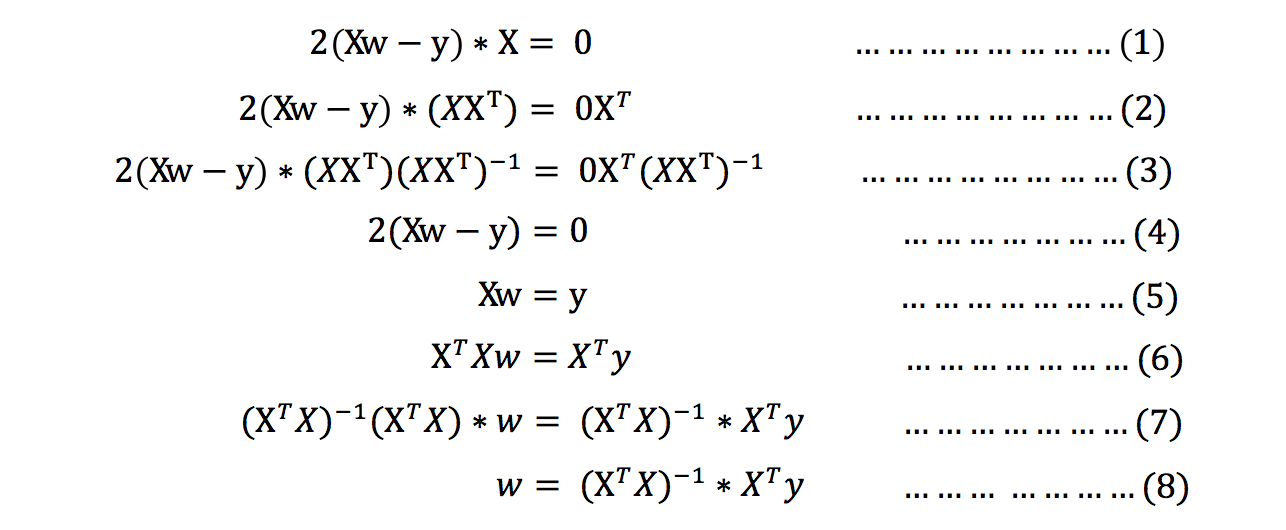
式(1)到式(2)推导过程中, X是一个m行n列的矩阵，并不能保证其有逆矩阵，但是右乘XT把其变成一个方阵，保证其有逆矩阵。式（5）到式（6）推导过程中，和上类似。

2.2 梯度下降(Gradient Descent)

2.2.1 什么是梯度下降

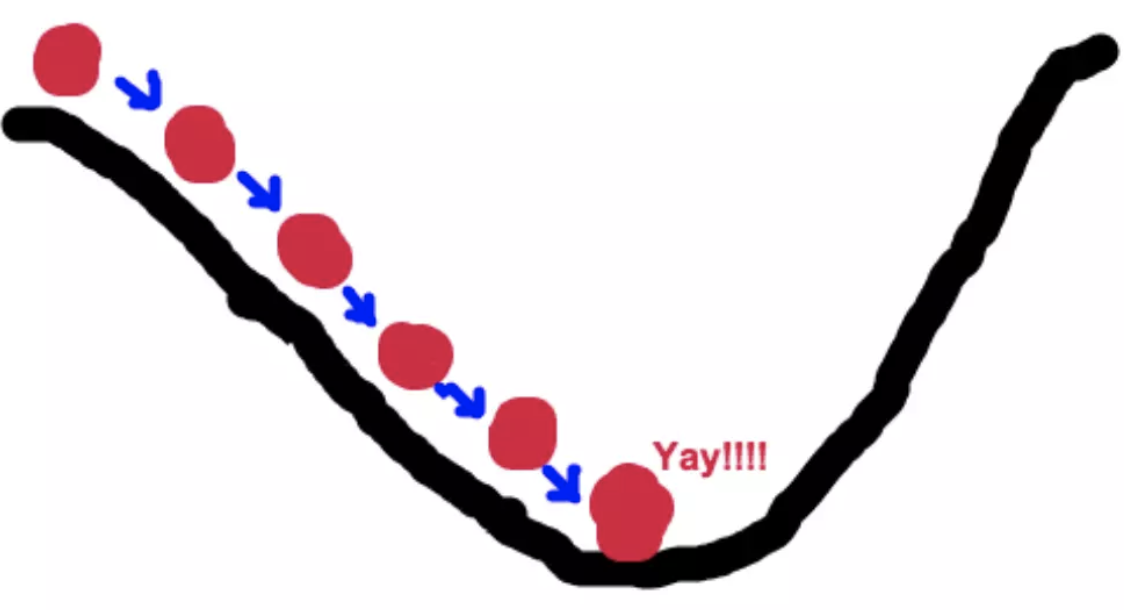
梯度下降的基本过程就和下山的场景很类似。

• 首先，我们有一个可微分的函数。这个函数就代表着一座山。
• 其次，我们的目标就是找到这个函数的最小值，也就是山底。

根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数值变化最快的方向。 所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。

2.2.2 梯度的概念

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率；

在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向；

我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点！

2.2.3 梯度下降举例

• 1. 单变量函数的梯度下降
  

如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底。

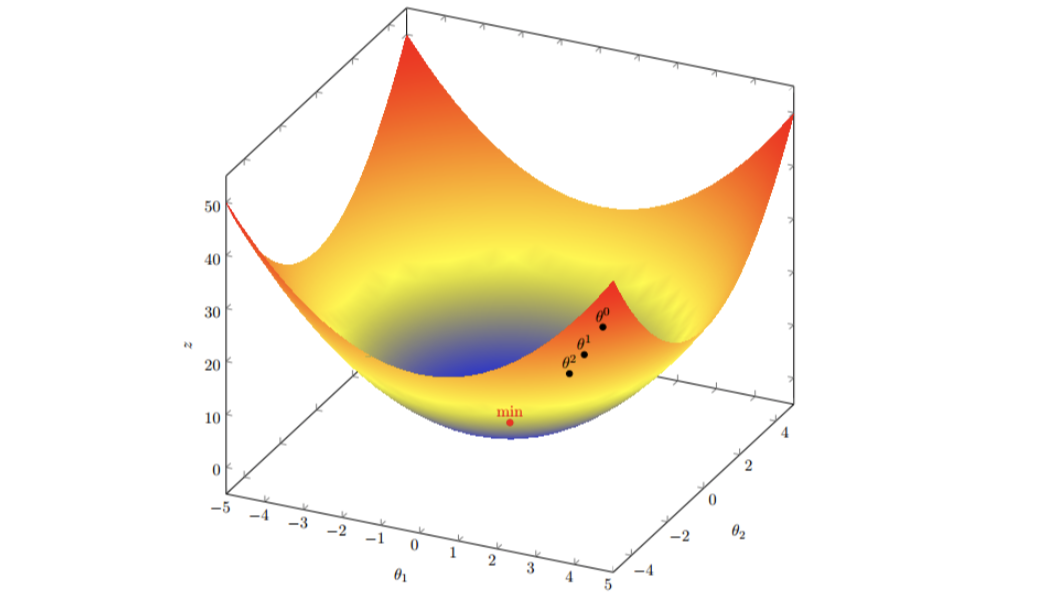
• 2.多变量函数的梯度下降
  
  
  我们发现，已经基本靠近函数的最小值点
  

2.2.4 梯度下降（Gradient Descent）公式

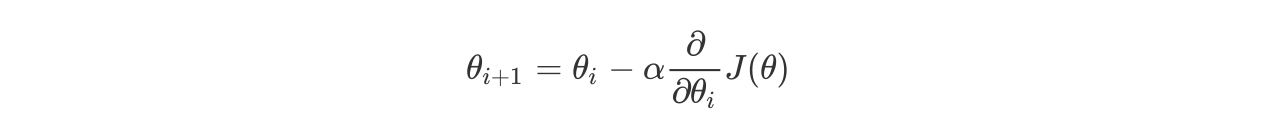
• α是什么含义？
  α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！
  
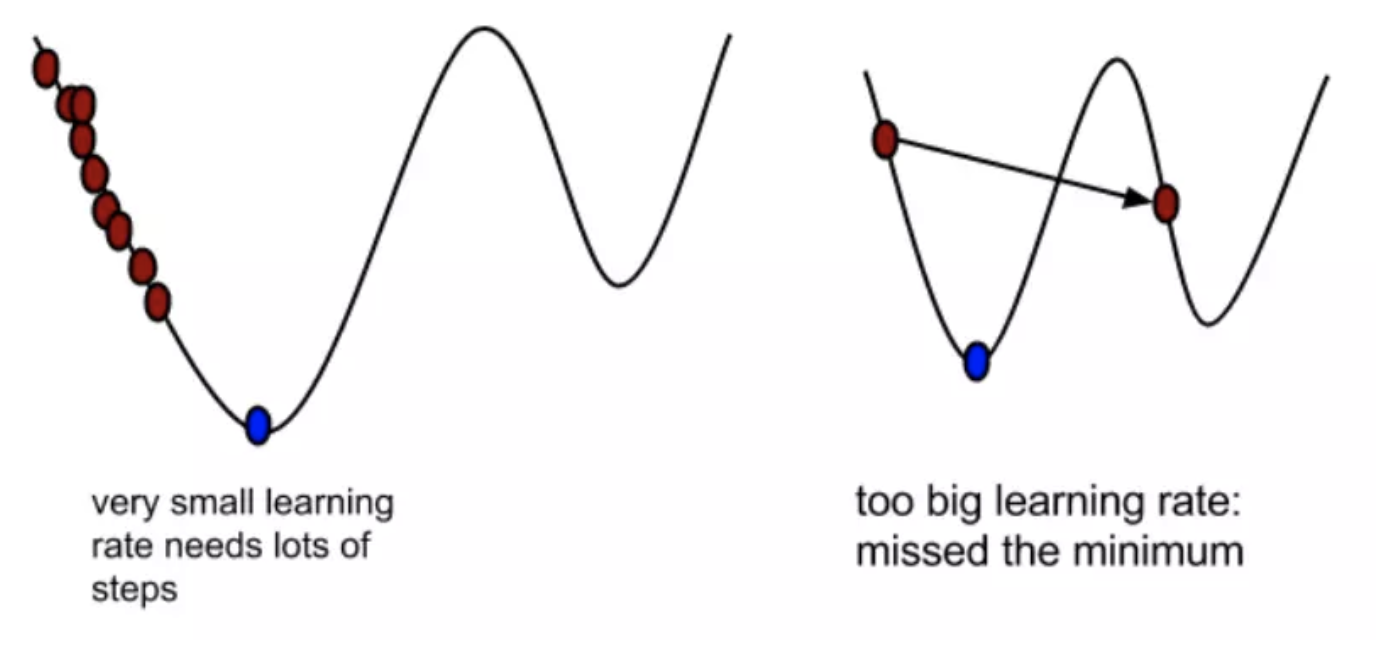
• 为什么梯度要乘以一个负号？
  梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号，通过两个图更好理解梯度下降的过程
  
  
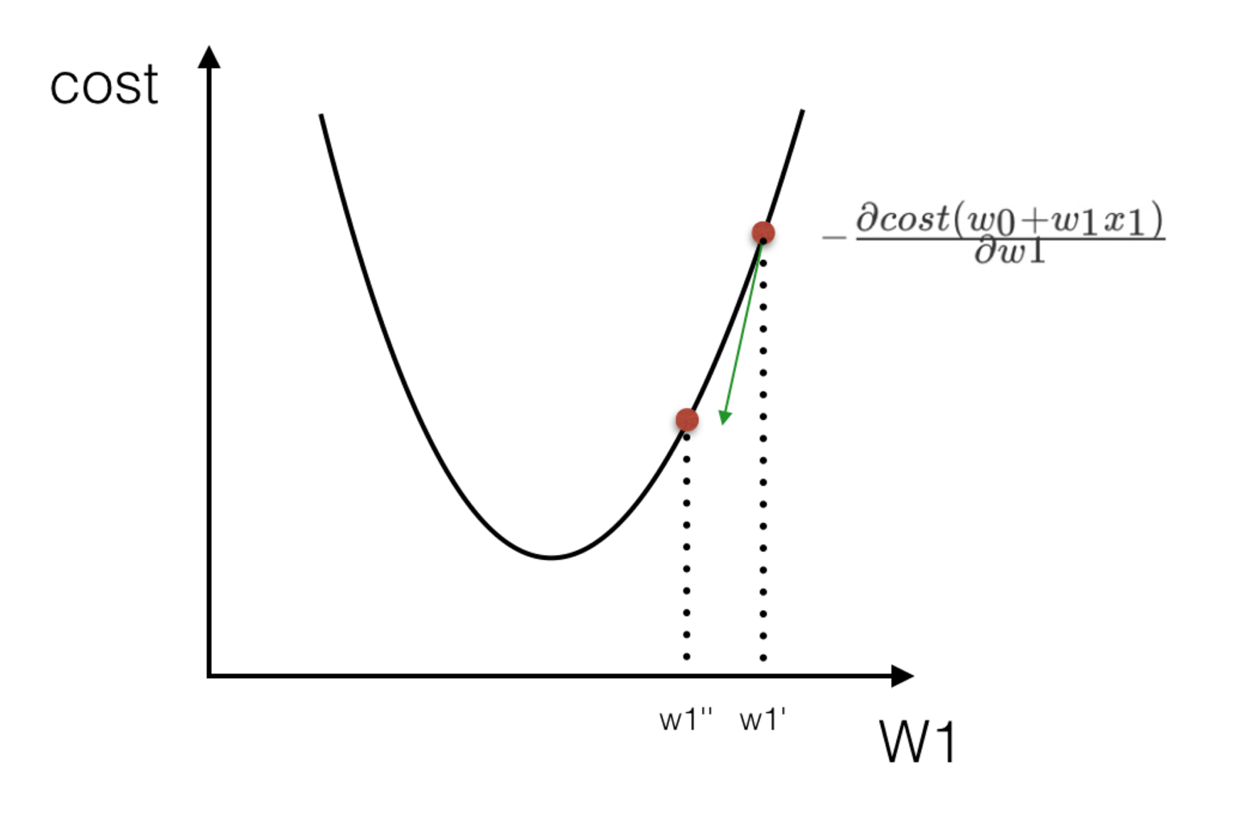
  有了梯度下降这样一个优化算法，回归就有了"自动学习"的能力
• 优化动态图演示
  

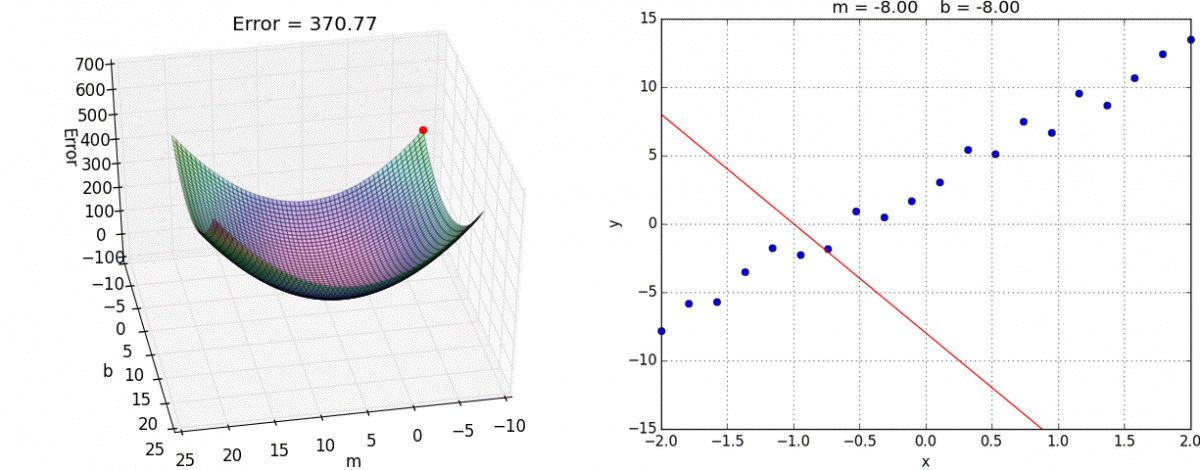
3 梯度下降和正规方程的对比

梯度下降	正规方程
需要选择学习率	不需要
需要迭代求解	一次运算得出
特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

3.1 算法选择依据：

• 小规模数据：
  • 正规方程：LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：
  • 梯度下降法：SGDRegressor