Python自然语言处理学习笔记(63):7.4 语言结构中的递归
7.4 Recursion in Linguistic Structure 语言结构中的递归
Building Nested Structure with Cascaded Chunkers 用逐位分块器构建嵌套结构
So far, our chunk structures have been relatively flat. Trees consist of tagged tokens, optionally grouped under a chunk node such as NP. However, it is possible to build chunk structures of arbitrary depth, simply by creating a multi-stage chunk grammar containing recursive rules. Example 7.10 has patterns for noun phrases, prepositional phrases, verb phrases, and sentences. This is a four-stage chunk grammar, and can be used to create structures having a depth of at most four.
|
||
|
||
Unfortunately this result misses the VP headed by saw. It has other shortcomings too. Let's see what happens when we apply this chunker to a sentence having deeper nesting. Notice that it fails to identify the VP chunk starting at.
|
The solution to these problems is to get the chunker to loop over its patterns: after trying all of them, it repeats the process. We add an optional second argument loop to specify the number of times the set of patterns should be run:
|
Note
This cascading process enables us to create deep structures. However, creating and debugging a cascade is difficult, and there comes a point where it is more effective to do full parsing (see Chapter 8). Also, the cascading process can only produce trees of fixed depth (no deeper than the number of stages in the cascade), and this is insufficient for complete syntactic analysis.
Trees 树
A tree is a set of connected labeled nodes, each reachable by a unique path from a distinguished root node. Here's an example of a tree (note that they are standardly drawn upside-down(颠倒的)):
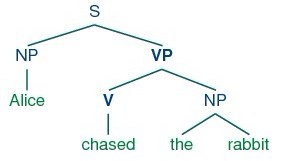
We use a 'family' metaphor(比喻) to talk about the relationships of nodes in a tree: for example, S is the parent of VP; conversely VP is a child of S. Also, since NP and VP are both children of S, they are also siblings(兄弟). For convenience, there is also a text format for specifying trees:
|
Although we will focus on syntactic trees, trees can be used to encode any homogeneous hierarchical structure(齐次分层结构) that spans a sequence of linguistic forms (e.g. morphological structure(形态结构), discourse structure(话语结构)). In the general case, leaves and node values do not have to be strings.
In NLTK, we create a tree by giving a node label and a list of children:
|
We can incorporate these into successively larger trees as follows:
|
Here are some of the methods available for tree objects:
|
The bracketed representation for complex trees can be difficult to read. In these cases, the draw method can be very useful. It opens a new window, containing a graphical representation of the tree. The tree display window allows you to zoom in and out, to collapse and expand subtrees, and to print the graphical representation to a postscript file(备注文件) (for inclusion in a document).
|
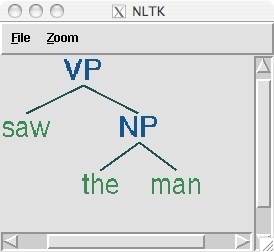
Tree Traversal 树遍历
It is standard to use a recursive function to traverse a tree. The listing in Example 7.11 demonstrates this.
|
||
|
||
Note
We have used a technique called duck typing(动态类型) to detect that t is a tree (i.e. t.node is defined).



 浙公网安备 33010602011771号
浙公网安备 33010602011771号