【abc401】DEFG

D

题意：

思路：
1.S中o相邻的问号全部改为.
2.找到S中能够填充的o的最大数量M
3.如果我完全足够了，直接输出S
​ 如果最多的刚刚好构造，偶数连续段保留?，奇数连续段构造o.
填充问题，贪心思考边界
下界：所有未知位置全部不填，就是cnto
上界：贪心将所有都填满，(L+1)/2
如果不超过K边界，我最多可以构造M个，> K， 所以任何位置我都能填或者不填，就是原来的S，????? o.o.o， .o.o..，（可以任意删除o位置）

代码：

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n, k, mx = 0, i, j, p, len; cin >> n >> k;
    string s, t; cin >> s, s += " "; //加入末尾哨兵！防止溢出/多次计算
    t = s;
    
    for(i = 0; i < n; i++){
        if(s[i] == 'o'){
            if(i>0) t[i-1] = s[i-1] = '.';
            if(i<n-1) t[i+1] = s[i+1] = '.';
            k--;
        }
    }

    if(k == 0){
        for(i = 0; i < n; i++)
        {
            if(s[i] == '?') t[i] = '.';
        }
        cout << t << '\n';
    }else{
        //尝试得到上界
        for(i = 0, j = 0; i <= n; i++){
            if(s[i] == '?')j++;
            else{
                mx += (j+1)/2;
                j = 0;
            }
        }
        //cout << k << ' ' << mx << '\n';
        if(k ==mx){
            for(int i = 0; i <= n; i++) {
                if(s[i] == '?') j++;
                else {
                    if(j & 1) {
                        for(int p = 1; p <= j; p++) {
                            t[i - p] = ".o"[p & 1];
                            // o.o.o.o
                        }
                    } else {
                        for(int p = 1; p <= j; p++) t[i - p] = '?';
                    }
                    j = 0;
                }
            }
        }else{
            for(i = 0; i < n; i++) if(s[i] == '?') t[i] = '?';
        }

        cout << t << '\n';
    }
    return 0;
}

E

题意：

思路：
就是看1~k这个连通块能不能恰好有这k个点，将所有与连通块相邻的边全部消除就是答案
可以用2个并查集来维护边，1个维护大小恰好为k的并查集，1个维护包含相邻边的并查集，
ans = 包含相邻边 - k
代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m;
struct disjoint_sets_union {
    int fa[N], sz[N];
    void init(){
        for(int i = 1; i <= n; i++){
            fa[i] = i;
            sz[i] = 1;
        }
    }

    int find(int x){
        return fa[x] == x ? x : fa[x] = find(fa[x]);
    }

    void merge(int u, int v){
        int x = find(u), y = find(v);
        if(x==y)return;

        if(sz[x] < sz[y]) swap(x,y);
        sz[x] += sz[y];
        fa[y] = x;
    }

    int getsz(int x){
        return sz[find(x)];
    }
} D, d;

vector<pair<int,int>> E[N], e[N];
int main()
{
    cin >> n >> m;
    for(int i = 0; i < m; i++)
    {
        int u, v;
        cin >> u >> v;
        E[max(u,v)].push_back({u,v});
        e[min(u,v)].push_back({u,v});
    }
    D.init(); d.init();
    for(int k = 1; k <= n; k++){
        //到了k时刻将所有的边全部放到连通块中
        for(auto [u,v] : E[k]) D.merge(u,v);
        for(auto [u,v] : e[k]) d.merge(u,v);

        //从1开始
        if(k == D.getsz(1)){
            cout << d.getsz(1) - k << '\n';
        }else{
            cout << -1 << '\n';
        }
    }

    return 0;
}

F

题意：

思路：
【经典结论】连接两棵树，新的树的直径一定是四个点当中的两个 -> 根据跨越或者不跨越分类讨论，新的直径的值 ∈ {已有直径的较大值，跨越后两边距端点较大距离相加的值}
然后就可以根据值域分类讨论了，dia = max(D, Ai + Bj + 1)

但是，对于每个i都去求和B[j]肯定会T，注意这里是值域，如果存在某个值使得对于每个i，都有 Ai + Bj + 1 > D，那么>B[j]的所有值天然不可能选择D
根据这个单调性，我们就可以用捅的方式在值域数组中统计后缀和，这样就能o(1)得到每个A[i]满足的Bj的和了

举个例子，按照我们的满足单调性的值域后缀统计和的思路就能画出下面这个数轴
假设我们当前B = {1,3,4,4}

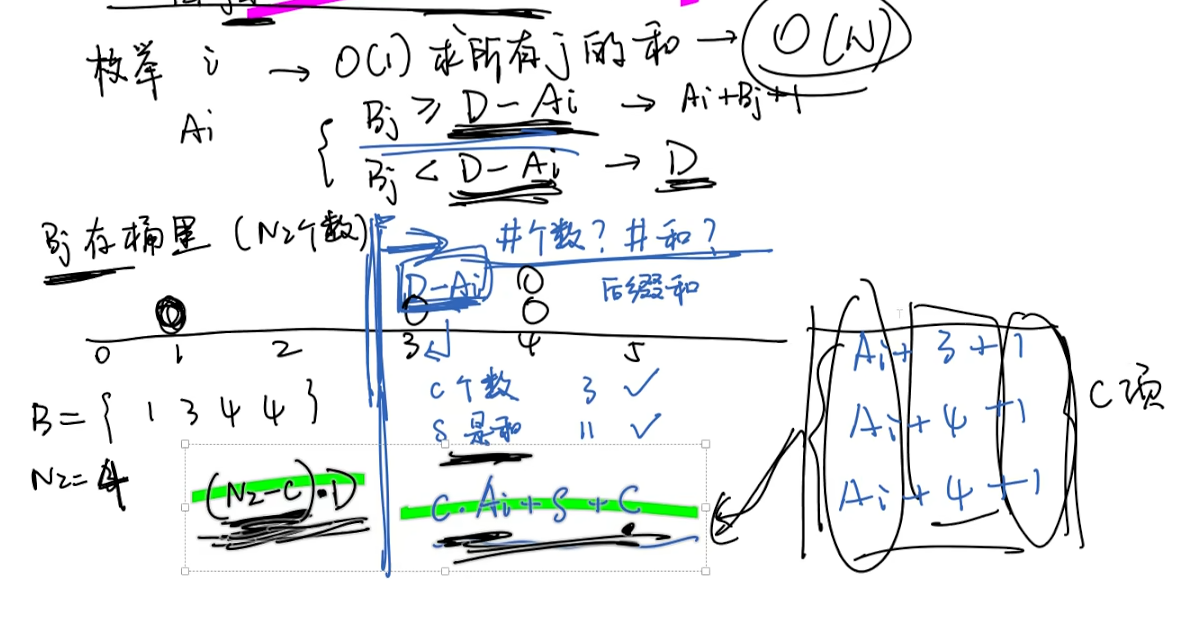
c是可以取到Ai+Bj+1这部分的点的个数，s就是后缀和，D是两棵树直径的最大值
转化为 -> ans += cA[i] + s + c + (n2 - c)D

到这里，这个题目的思路就结束了，接下来是代码部分，分为以下几块：
1.求解树的直径，两棵树直径的最大值
2.求解两棵树每个点到直径两个端点的较大值
3.求解值域数组转化后的后缀和以及数字个数
4.统计ans，注意long long

代码：

/*
1.树的直径 pair<int,int> res = {1,u} //结点个数 res = {0,u} //最远距离
2.乘法就要强转ll
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
int n1, n2, A[N], B[N], D, dep[N], suf_c[N], u, v, c;
ll suf_s[N], ans, s;
vector<int> G[N];

//dfs -> {距离, 最远的点}
pair<int, int> dfs(int u, int fa)
{
    pair<int, int> res = {0,u}; //细节错误1
    for(auto v : G[u])
    {
        if(v == fa) continue;
        dep[v] = dep[u] + 1;
        auto pi = dfs(v, u);
        pi.first += 1;
        res = max(res, pi);
    }
    return res;
}

void solve(int *d, int n)
{
    dep[1] = 0;
    auto [dis1, u] = dfs(1,0); //1 到达直径的一个端点u 
    dep[u] = 0;
    auto [dis2, v] = dfs(u,0); //u 到达直径另外一个端点 v， dep[i]，i到达u的最大距离
    
    D = max(D, dis2);

    memcpy(d, dep, sizeof dep);
    
    dep[v] = 0;
    dfs(v,0);

    for(int i = 1; i <= n; i++)
    {
        d[i] = max(d[i], dep[i]);
    }
}

int main()
{
    cin >> n1;
    for(int i = 0; i < n1-1; i++)
    {
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }

    solve(A,n1); //A[i]到达端点的最远距离
    
    for(int i = 1; i <= n1; i++)G[i].clear();

    cin >> n2;
    for(int i = 0; i < n2-1; i++)
    {
        cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    
    solve(B,n2);

    //根据距离分类，放到捅里面玩后缀
    //树上问题 -> 在值域数组上求和
    for(int i = 1; i <= n2; i++)
    {
        suf_c[B[i]]++;
        suf_s[B[i]] += B[i];
    }

    //求解后缀信息，距离值域上界是D
    for(int i = D - 1; i >= 0; i--)
    {
        suf_c[i] += suf_c[i+1];
        suf_s[i] += suf_s[i+1];
    }

    //统计答案
    ans = 0;
    for(int i = 1; i <= n1; i++)
    {
        c = suf_c[D - A[i]];
        s = suf_s[D - A[i]];
        ans += (ll)c * A[i] + s + c + (ll)(n2-c) * D; //细节错误2
    }

    cout << ans << '\n';

    return 0;
}

G

题意：

思路：
【涨知识】二分，最大流二分图最大匹配
Dinic求解最大流，汇点流入管道为n，则完美匹配
由于我没有学习最大流，暂时也没打算，所以用的匈牙利
放个最大流代码：https://atcoder.jp/contests/abc401/submissions/64828019

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using lll = __int128;
const int N = 3e2 + 10;
ll sx[N], sy[N], gx[N], gy[N];
lll d2[N][N], r2;
vector<int> G[N];
int n, vis[N], match[N];

lll dis(ll x1, ll y1, ll x2, ll y2){
    lll dx = x2 - x1;
    lll dy = y2 - y1;
    return dx*dx + dy*dy;
}

//二分图匹配：对没查看的点，如果没有分配，就配上去，否则，换一个再配
bool dfs(int u)
{
    for(auto v : G[u])
    {
        if(!vis[v])
        {
            vis[v] = 1;
            if(match[v] == -1 || dfs(match[v])){
                match[v] = u;
                return true;
            }
        }
    }
    return false;
}

bool check(lll x)
{
    for(int i = 0; i < n; i++) G[i].clear();
    //二分图
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++){
            if(d2[i][j] <= x) G[i].push_back(j);
        }

    //匹配
    int cnt = 0;
    memset(match, -1, sizeof match);
    for(int i = 0; i < n; i++){
        memset(vis, 0, sizeof vis); //每次都从头看过，以便于交换
        if(dfs(i))cnt++; //找到了匹配
    }
    return cnt == n;
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++) cin >> sx[i] >> sy[i];
    for(int i = 0; i < n; i++) cin >> gx[i] >> gy[i];

    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
        {
            d2[i][j] = dis(sx[i], sy[i], gx[j], gy[j]);
        }

    lll l = 0, r = 2 * 1e18 * 1e18;
    while(l < r){
        lll mid = (r + l) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }

    long double ans = sqrtl((long double) l);
    printf("%.10Lf\n", ans);
    return 0;
}

日常多一嘴：
这场题目昨天补了一天，今天上午才全部补完，主要是昨天又去搞环境白费了2hQAQwww