组合数学 —— 容斥原理1

2025.4.16
这个大坑，我今天总算是找到解法了，真知识，还得从书中得来啊！前提是有耐心，能看懂，讲得明白~
（本文基本不存在严谨的数学证明/数学定理/数学论述，谨慎食用）

（前置知识：朴素集合论，将集合的基本概念过一遍才能真正透彻这里讲的到底是个什么东西，概念是一切的基石，永恒真理，不可违背，后果自负）

大白话总结容斥原理：

• 是一个计数方法，不重不漏的计算所有数字
• 能算到满足性质p1,p2...pm至少一条性质的元素个数（容斥原理保证了全集S中每个元素x对于性质的计数只贡献了一次）
• 是一个公式， 是对n个集合的集合族中的每一个非空子集的交，每个元素都存在一项被计数
• 扩展形式：用于计算不满足p1,p2,..pm所有性质的元素个数，（总数 - 至少满足一条 = 所有都不满足）

于是乎，就能得到两个折磨我2个月的公式：
from:知乎

我们从一道例题来理解：
1.求解约束方程的整数解个数：x1 + x2 + x3 = 11
(x1,x2,x3为非负整数，且x1 <= 3，x2 <= 4，x3 <= 6)

解决这个问题之前，我们先来看一个推论
排列组合推论2：n 个元素的集合中允许出现重复的r组合有C(n - 1 + r, r) = C(n-1 + r, n - 1)种组合
7种类型纸币选择5张，有多少种方案数？
| | | | | | * * * * *
不同类型可以用6个隔板隔开
选择5个元素，用5个星星表示
那么，总方案数可以理解为，在11个位置中选择5个位置放置星星的方案数，即ans = C(11, 5)

4种类型的甜点，选择6个甜点有多少种方案数？
同理：
| | | * * * * * *
在10个位置中选择6个位置放置星星的方案数

于是，方程的解总组合个数翻译为：
3种数字，放置11个1有多少种方案数？ （其实抽象到实际物品每个物品也是1，所以这里基数是1）
| | * * * * * * * * * * *
在13个位置中选择11个位置放置11个星星的方案数C(13, 11) = 78

ok，至此，我们知道了该方程的解的全集个数S
这是个计数问题，知道了全集个数，让我们求解满足一些性质的元素个数，
这里是全部性质都要满足，所以不考虑经典容斥原理，而是他的拓展形式
于是，答案 = 总的解的个数 - N(p1p2p3)（至少满足一条的解的个数）
也可以反着定义求解
p1'：x1 > 3，p2'：x2 > 4，p3'：x3 > 6

N(p1'p2'p3') = S - |A1 ∪ A2 ∪ A3|（不具备p1p2p3中的任何一条性质就是答案）
计算过程：

例题1：CCPC2021区域赛（威海）M题810975

求解长度为 n 的 01 串，恰好有 m 个 1，且最长 1 连续段长度恰好为 m 的方案数。

思路：
定义最长段连续1 <= k的方案数为f(k)，ans = f(k) - f(k-1)

1段的长度和为m，
每个段的最大值为k
最多可以有n-m+1连续1段（连续0已经考虑）

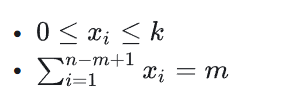
然后就是模型了，对不符合约束条件的方案数枚举，容斥计数
转化为无约束模型：方程两边 - j * (k+1)，然后计数

代码：我

点击查看代码

#include <bits/stdc++.h>
using namespace std;

#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)

typedef long long LL;

constexpr int N = 1e6 + 10, md = 998244353;
LL fpow(LL a, int b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1)
            res = res * a % md;
        a = a * a % md;
        b >>= 1;
    }
    return res;
}

LL fac[N], ifac[N];
void init(int n)
{
    fac[0] = 1;
    rep(i, 1, n)
        fac[i] = fac[i - 1] * i % md;
    ifac[n] = fpow(fac[n], md - 2);
    dwn(i, n, 1)
        ifac[i - 1] = ifac[i] * i % md;
}

LL C(int n, int k)
{
    if(n < k || k < 0)
        return 0;
    return fac[n] * ifac[k] % md * ifac[n - k] % md;
}

int n, m, k;

LL cal(int n, int m)
{//不定方程总和为m，无约束时，方案数
    return C(m + n - 1, n - 1);
}

LL f(int n, int m, int k)
{// n个数总和为m，xi <= k
    LL res = 0;
    rep(i, 0, n)
    {
        int coef = (i & 1) ? -1 : 1; //容斥系数
        LL tmp = coef * C(n, i) * cal(n, m - i * (k + 1)) % md;
        //选i个违反约束，不定方程总和为m - i * (k + 1)
        res = (res + tmp) % md;
    }
    return res;
}

void solve()
{
    cin >> n >> m >> k;
    cout << ((f(n - m + 1, m, k) - f(n - m + 1, m, k - 1)) % md + md) % md << '\n';
    // (最长1<=k的方案数) - (最长1<=k-1的方案数)
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    cout.tie(0);
    init(N - 10);
    solve();
}

今天就先到这里吧，因为我看了一下下一题题解，可能已经超过了我目前能掌握的范围了，能把板子理解已经可以了，就目前而言

参考资料：
离散数学及其应用（第7版）
知乎