关于我在2025蓝桥杯上面没有做出来树形dp背包这件事

2025.4.12
一个具有历史意义的日子，大一第一次参加蓝桥杯，双非本科，AI专业。
总体感受可以用以下几个关键词描述：

• 蓝桥省赛 == cf div3
• 短板的组合数学和树形dp被创了，这两个真的是我做了这么久的题目的噩梦
• 但是，一句话，说白了，还是做得少了，想得少了，平时没有认真写解题报告，每天虽然写了不少题目，想了不少，但是，实际上都没到点子上，我就觉得自己平时训练有点虚，原来我是该做得没做到位啊。写总结，回顾复习，理解代码，复现代码...都没做好
  最后，反正就是不咋地，
  接下来还是该干嘛干嘛，好好记录
  记录下目前为止这个小子为了算法竞赛抛弃了很多，他都干了些什么？
  
  
  
  牛客、hdu、leetcode好久没写了，cf上瘾但是真正解题数目也不达标...
  所以我这3个月到底在干嘛...跟混日子有什么区别？

我来写解题报告了
（后天就有结课考试了，我还在这里...）

G：树形dp —— 背包
题意：
统计删点后最大合法子树和，注意子集和问题
思路：
"树上背包"：
定义：dp[u][i]: 表示以u为根节点i为背包容量可达(true)
初始化：dp[u][0] = true，表示将子树整个切除和为0可达
转移：
枚举u的所有可能贡献值x，枚举v的所有贡献值y，（背包合并过程很重要！）
代码：

点击查看代码

/*
树上背包：（核心：合并过程）
背包合并过程：
1.枚举所有x目前可能的贡献
2.枚举所有子节点y能给到的贡献
3.每枚举完一个子节点v后更新合并背包

*/
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int n;
vector<int> w;
vector<vector<bool>> dp;
vector<vector<int>> g;

void dfs(int u, int fa){
    dp[u].assign(w[u] + 1, 0);
    dp[u][0] = 1;
    bool isleaf = 1;
    for(auto v : g[u]){
        if(v == fa) continue;
        isleaf = 0;
        dfs(v,u);
        
        vector<bool> ndp(w[u]+1, false);
        for(int x = 0; x <= w[u]; x++){
            if(!dp[u][x]) continue;
            for(int y = 0; y < dp[v].size(); y++){
                if(!dp[v][y])continue;
                if(x + y <= w[u]) ndp[x + y] = 1;
            }
        }
        dp[u] = ndp; // 合并子树，用于计算子集和（标记贡献法）
    }

    if(isleaf){
        dp[u][w[u]] = 1;
    }
}

int main(){
    cin >> n;
    w.resize(n+1); dp.resize(n+1); g.resize(n+1);
    for(int i = 1; i <= n; i++) cin >> w[i];

    for(int i = 0; i < n - 1; i++){
        int u,v; cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    int ans = 0;
    dfs(1, 0);

    for(int i = 0; i <= w[1]; i++){
        if(dp[1][i]) ans = i;
    }
    cout << ans << '\n';
    return 0;
}

我们再来看一道：P3698
（没什么关系，只是加训一道）
题意：
在n个结点的树上可以走m步，可以重复经过结点，问最多能经过多少结点？
思路：01背包 + 状态标记
模拟发现，可能会往回走 -> 加一位标记是否要回来（状态机dp）
进一步分析，对于每个结点，只有3种可能，
1.往下走到黑
2.往下走又回到根节点
3.往儿子走到黑，不回来

主要看0/1分类标记回不回来
定义：dp[u][i][0]：根节点u走i步不回到根节点经过的最多结点数，dp[u][i][1]：回到根节点的经过最多结点数
初始化：dp[u][0][0] = dp[u][0][1] = 1 // 以u为根往下走0步经过1个结点（自己）
转移：
不回到根节点0：

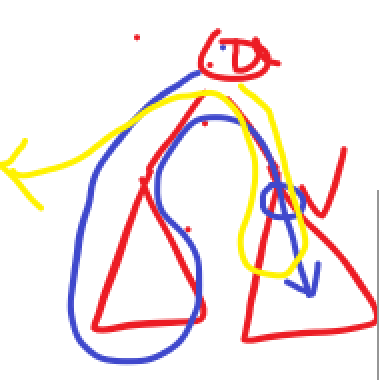
如图：两种情况：1.经过v从u离开 2.经过u从v离开
所以，可得转移：
dp[u][i][0] = max(dp[u][i - k][0] + dp[v][k-2][1], dp[u][i-k][1] + dp[v][k-1][0]); // 经过v回到u，耗费2步，v只剩下k-2步了；经过u从v离开，只有1条经过v和u的边
回到根节点1：
dp[u][i][1] = max(dp[u][i-k][1] + dp[v][k-2][1])
代码：

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int MAXV = 205;
const int NEG = -1000000000;
int n, k;
vector<int> g[MAXV];
int dp[MAXV][MAXV][2];
 
void dfs(int u, int parent) {
    for (int j = 0; j <= k; j++) {
        dp[u][j][0] = dp[u][j][1] = NEG;
    }
    dp[u][0][0] = dp[u][0][1] = 1;
    
    for (int v : g[u]) {
        if (v == parent) continue;
        dfs(v, u);
        int newdp[MAXV][2];
        for (int j = 0; j <= k; j++) {
            newdp[j][0] = newdp[j][1] = NEG;
        }
        for (int j = k; j >= 0; j--) {
            for (int t = 0; t <= j; t++) {
                if (t >= 2 && dp[u][j - t][0] != NEG && dp[v][t - 2][1] != NEG)
                    newdp[j][0] = max(newdp[j][0], dp[u][j - t][0] + dp[v][t - 2][1]);
                if (t >= 1 && dp[u][j - t][1] != NEG && dp[v][t - 1][0] != NEG)
                    newdp[j][0] = max(newdp[j][0], dp[u][j - t][1] + dp[v][t - 1][0]);
                if (t >= 2 && dp[u][j - t][1] != NEG && dp[v][t - 2][1] != NEG)
                    newdp[j][1] = max(newdp[j][1], dp[u][j - t][1] + dp[v][t - 2][1]);
            }
        }
        for (int j = 0; j <= k; j++) {
            dp[u][j][0] = newdp[j][0];
            dp[u][j][1] = newdp[j][1];
        }
    }
}
 
int main(){
    scanf("%d%d", &n, &k);
    for (int i = 1; i < n; i++){
        int u, v;
        scanf("%d%d", &u, &v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    
    dfs(0, -1);
    int ans = 0;
    for (int j = 0; j <= k; j++){
        ans = max(ans, dp[0][j][0]);
    }
    printf("%d\n", ans);
    return 0;
}

（gpt生成，我要赶紧复习了，run~）