***该文献对分支决策探讨的角度十分新颖!
Understanding VSIDS Branching Heuristics in Conflict-Driven Clause-Learning SAT Solvers
Abstract
|
Conflict-Driven Clause-Learning (CDCL) SAT solvers crucially depend on the Variable State Independent Decaying Sum (VSIDS) branching heuristic for their performance. Although VSIDS was proposed nearly fifteen years ago, and many other branching heuristics for SAT solving have since been proposed, VSIDS remains one of the most effective branching heuristics. Despite its widespread use and repeated attempts to understand it, this additive bumping and multiplicative decay branching heuristic has remained an enigma. |
|
|
In this paper, we advance our understanding of VSIDS by answering the following key questions.
The first question we pose is “what is special about the class of variables that VSIDS chooses to additively bump?” 译文:VSIDS选择添加的变量有什么特殊之处? In answering this question we showed that VSIDS overwhelmingly picks, bumps, and learns bridge variables, defined as the variables that connect distinct communities in the community structure of SAT instances. This is surprising since VSIDS was invented more than a decade before the link between community structure and SAT solver performance was discovered.译文:在回答这个问题时,我们展示了VSIDS压倒性地选择、碰撞和学习桥梁变量,桥梁变量被定义为在SAT实例的社区结构中连接不同社区的变量。 Additionally, we show that VSIDS viewed as a ranking function correlates strongly with temporal graph centrality measures.译文:此外,我们表明VSIDS被视为一个排序函数,与时间图中心性测度密切相关。 Putting these two findings together, we conclude that VSIDS picks high-centrality bridge variables.译文:将这两个发现结合在一起,我们得出结论,VSIDS选择了高中心性桥接变量。
The second question we pose is “what role does multiplicative decay play in making VSIDS so effective?”译文:在使VSIDS如此有效的过程中,乘法衰变起了什么作用? We show that the multiplicative decay behaves like an exponential moving average (EMA) that favors variables that persistently occur in conflicts (the signal) over variables that occur intermittently (the noise). 译文:我们表明,乘法衰减表现得像指数移动平均线(EMA),它倾向于持续发生冲突的变量(信号),而不是间歇发生的变量(噪声)。
The third question we pose is “whether VSIDS is temporally and spatially focused.” 译文:VSIDS是否在时间和空间上集中。 We show that VSIDS disproportionately picks variables from a few communities unlike, say, the random branching heuristic. 译文:我们表明VSIDS不成比例地从少数群体中选择变量,不像随机分支启发式。 We put these findings together to invent a new adaptive VSIDS branching heuristic that solves more instances than one of the best-known VSIDS variants over the SAT Competition 2013 benchmarks.译文:我们将这些发现放在一起,发明了一种新的自适应VSIDS分支启发式,它解决的实例比2013年SAT竞赛中最著名的VSIDS变种之一还要多。 |
|
Keywords
Boolean Formula Exponential Smoothing Eigenvector Centrality Decay Factor
1 Introduction
|
The Boolean satisfiability (SAT) problem [14] is the quintessential NP-complete problem, a class of decision problems conjectured to be computationally hard. Yet, impressively, modern sequential Conflict-Driven Clause-Learning SAT solvers [6, 9, 15, 32, 34] are able to solve large instances obtained from real-world applications [3, 29]. Although hundreds of techniques and heuristics have been proposed over the last five decades to solve the Boolean SAT problem [2, 3], modern SAT solvers rely crucially only on a handful of them. Of these, the two most important are Conflict-Driven Clause-Learning with backjumping (CDCL) [34] and Variable State Independent Decaying Sum (VSIDS) branching heuristic [36]. 译文:其中最重要的两个是冲突驱动的clause-learning和backjumping (CDCL)[34]和变元状态独立衰减和(VSIDS)分支启发式[36] |
|
|
Many systematic experiments have been performed to ascertain the veracity of this observation [29]. Additionally, not only is VSIDS one of the most effective branching heuristics, but many other well-known high-performing branching heuristics are simply variants of VSIDS. Researchers have proposed some theoretical explanations for the impact of clause-learning on the performance of the modern SAT solvers: clause-learning allows SAT solvers to polynomially simulate general resolution propositional proof system [5, 7, 39]. 译文:研究人员对clauses -learning对现代SAT求解器性能的影响提出了一些理论解释:clauses -learning允许SAT求解器多项式地模拟一般求解命题证明系统[5,7,39]。 |
|
|
However, our understanding of the role played by VSIDS heuristic has previously been limited. 译文:然而,我们对VSIDS启发式所扮演的角色的理解以前是有限的。 The motivation for the research presented in this paper is to achieve a better scientific understanding of VSIDS. 译文:本文提出的研究动机是为了更好地理解VSIDS。 We focus on two well-known variations of VSIDS, namely cVSIDS and mVSIDS, described in Sect. 2. |
|
|
Contribution IV: Exponential Moving Average and Multiplicative Decay in VSIDS.VSIDS中的指数移动平均和乘法衰减。 Fourth, we show that the multiplicative decay in VSIDS is a form of exponential moving average, and provide a plausible explanation as to why this is crucial to the effectiveness of VSIDS.译文:我们证明了VSIDS中的乘法衰减是指数移动平均的一种形式,并提供了一个合理的解释,为什么这对VSIDS的有效性至关重要。 |
|
|
Contribution V: A Novel Adaptive Branching Heuristic. Our findings led to a new VSIDS called adaptVSIDS that adapatively adjusts the exponential moving average (a form of adaptive moving average) depending on the quality of the learnt clauses. We show that adaptVSIDS outperforms mVSIDS, by solving 2.4 % more instances over the SAT Competition 2013 benchmarks. 译文:调整指数移动平均(自适应移动平均的一种形式)取决于学习的子句的质量。 |
|
5 Contribution IV: Exponential Moving Average and Multiplicative Decay
|
In this section, we argue that the multiplicative decay aspect of the VSIDS branching heuristic is a form of exponential moving average (EMA) [11]. 译文:VSIDS分支启发式的乘法衰减方面是指数移动平均(EMA)[11]的一种形式。 It is the inclusion of multiplicative decay in VSIDS that gives it its distinctive feature of focusing its search based on recent conflicts. 译文:VSIDS中包含了乘法衰减,这使它具有了将搜索重点放在最近冲突上的独特特征。T he original Chaff paper [36] and patent [35] rather cryptically mentioned that VSIDS acts like a “low-pass filter”. VSIDS就像一个“低通滤波器”。 They do not specify what signals are being fed to this filter, and why the high-frequency components are being filtered out and discarded.译文:他们没有具体说明什么信号被送入这个过滤器,以及为什么高频成分被过滤和丢弃。 |
|
|
In his paper [8], Armin Biere was perhaps the first to articulate the idea that additive bumping of variable scores can be viewed as a signal (a square wave, to be more precise) over the run of the solver.译文:Armin Biere首次阐明,在求解器运行中,变元分数的叠加碰撞可以被视为一个信号(方波,更准确地说)。 More precisely, at every time step, the signal of a variable is 1 if it is bumped, or 0 otherwise. Armin Biere formalized normalized VSIDS [8] as
sn is the normalized VSIDS activity of a variable v after the nth conflict. δk=1 if variable v was bumped in the kth conflict, otherwise δk=0. f is the decay factor. |
|
| While Huang et al. [26] referred to VSIDS as an EMA, we will show this explicitly. We not only characterize VSIDS as an EMA explicitly, but also describe why this is crucial to the effectiveness of VSIDS as a branching heuristic. In the next section we leverage this connection between EMA and VSIDS to propose an adaptive VSIDS branching heuristic inspired by an adaptive version of EMA. | |
|
EMA is a form of exponential smoothing, used in getting rid of noise (variables whose VSIDS scores are akin to high-frequency signals) in time series data (the signals due to VSIDS scores). Exponential smoothing is a class of techniques to mitigate the effect of random noise in time series data for the purpose of analysis and forecasting. Armin Biere’s normalized VSIDS equation can be rewritten to the following recursive formula:
This formula fits exactly the definition of Brown’s simple exponential smoothing, also known as exponential moving average. Therefore normalized VSIDS is exactly an EMA over the δδ time series. The EMA causes VSIDS to favor variables that “persistently” occur in “recent” conflicts.
Variables that occur persistently in “recent” conflicts could be a good guess for the root cause of those conflicts. Hence, perhaps the most effective search strategy is to focus on determining this root cause.译文:在“最近”冲突中持续发生的变量可能是对这些冲突根源的很好的猜测。因此,也许最有效的搜索策略是专注于确定这个根本原因。 The learnt clauses that result from such a strategy improve in quality with time, until such time that the root cause of a set of faulty judgment has been determined and enshrined as a learnt clause.译文:随着时间的推移,由这种策略产生的习得条款的质量不断提高,直到一系列错误判断的根本原因被确定下来,并被奉为习得条款。 |
|
6 Contribution V: A Faster Branching Heuristic Based on Adaptive Moving Average
| In this section, we report on our design of a better VSIDS based on the knowledge that VSIDS decay is a form of EMA. The EMA is integral to VSIDS performance as a branching heuristic, and now that the connection between EMA and VSIDS is established, all the literature on EMA and other time series data analysis are directly applicable to VSIDS.译文:所有关于EMA和其他时间序列数据分析的文献都直接适用于VSIDS。 | |
|
Adaptive Moving Average. Given that VSIDS decay is a form of EMA, we studied the literature of EMA from the financial domain [31], where it is known that the fixed decay factor can be undesirable. A moving average with a large decay factor would lag behind fast moving markets whereas a small decay factor would fail to smooth out a lot of noise.译文:衰减系数大的移动平均线会落后于快速波动的市场,而衰减系数小的移动平均线则无法消除大量的噪音。
Kaufman [31] noted that a fixed decay factor performs poorly when the market volatility changes. 译文:Kaufman[31]指出,固定衰减因子在市场波动性变化时表现不佳。 He devised adaptive moving average where the decay factor (also known as smoothing constant) is determined by the market volatility to minimise lag and noise.译文:他设计了自适应移动平均线,其中衰减因子(也称为平滑常数)由市场波动决定,以最小化滞后和噪声。 By fluctuating the decay factor when necessary, adaptive moving average is better than EMA at uncovering trends in the market.译文:通过在必要时波动衰减因子,自适应移动平均线在揭示市场趋势时优于均线。 |
|
|
Just like how markets can go up and down, a CDCL SAT solver can go up and down in “productivity” over time. 译文:就像市场上下波动一样,CDCL求解器的“生产率”也会随着时间上下波动。 For example, Audemard and Simon [6] discovered that a learnt clause with lower literals blocks distance (LBD) [6] is of higher quality.译文:具有较低文字块距离(LBD)[6]的学习子句具有较高的质量。 LBD of a clause is defined to be the number of decision levels that its variables span.译文:子句的LBD被定义为其变量所跨越的决策级别的数量。 If the solver is in a search space that produces many learnt clauses with low LBD, then we want to encourage the solver to stay within that search space.译文:如果求解器所处的搜索空间产生了很多低LBD的学习子句,那么我们希望鼓励求解器留在该搜索空间内。--如何鼓励?见下面说明,如当前冲突分析的得到学习子句的lbd小,则将decay设置为接近于1,增量间距变小,ceil不变(例如保持1e100)活跃度增量溢出衰减操作推迟,阶段性除以1e100操作的间隔加长。 We do so by adjusting the VSIDS decay factor to be closer to 1, i.e., decay slower. On the other hand, if the solver is in a search space that produces many learnt clauses with high LBD, it is best to choose a smaller decay factor, i.e., decay faster. Based on this insight, we devised a new VSIDS heuristic called adaptVSIDS by extending mVSIDS with an adaptive moving average. adaptVSIDS maintains a floating-point number lbdema equal to the exponential moving average of the learnt clause LBDs. 译文:adaptVSIDS保持一个浮点数lbdema等于learn子句LBDs的指数移动平均值。 lbdema is updated after every learnt clause and this number will be used to adjust the decay factor of the variables’ activities. In mVSIDS, the variables’ activities are decayed by multiplying with a constant decay factor, typically 0.95, after each conflict. Whereas in adaptVSIDS, the decay factor is adjusted based on the LBD of the learnt clause. If the LBD of the learnt clause is greater than lbdema, then use a decay factor of 0.75, otherwise use a decay factor of 0.99. Our website has all the code.译文:在mvsid中,变量的活动在每次冲突后通过乘以一个恒定的衰减因子(通常为0.95)来衰减。而在adaptVSIDS中,衰减因子是根据学习子句的LBD来调整的。如果learned子句的LBD大于lbdema,则使用0.75的衰减因子,否则使用0.99的衰减因子。我们的网站上有所有的代码。 |
|
| Experimental Setup and Methodology. The experiments were performed on the application and combinatorial categories of the SAT Competition 2013. For each instance with a timeout of 5000 seconds as per competition rules, we ran an unmodified MiniSAT 2.2.0 and a modified MiniSAT 2.2.0 with adaptVSIDS on StarExec [1]. | |
| Results and Interpretations. Our adaptVSIDS solved 351 instances whereas mVSIDS solved 343 instances, an increase of 2.4 % more solved instances. | |
7 Interpretation of Results
| We began our research by posing a series of questions regarding VSIDS, and we now interpret the results obtained in light of these questions.译文:我们通过提出一系列关于VSIDS的问题来开始我们的研究,现在我们根据这些问题来解释得到的结果。 | |
|
What is special about the class of variables that VSIDS chooses to additively bump? (Answered by Contributions I and III.) In the bridge variables experiment (Sect. 3), we showed that VSIDS disproportionately favored bridge variables. 译文:VSIDS选择添加的变量有什么特殊之处?译文:我们证明了VSIDS不成比例地偏爱桥变量。 Even though SAT instances have large number of bridge variables on average, the frequency with which VSIDS picks, bumps, and learns bridge variables is much higher. 译文:尽管SAT实例平均有大量桥接变量,但VSIDS选择、碰撞和学习桥接变量的频率要高得多。 There is no a priori reason to believe that VSIDS would behave like this. This surprising result, plus a previous result that good community structure correlates with faster solving time [38], suggests CDCL solvers exploit community structure. 译文:再加上之前的一个结果,即良好的社区结构与更快的解决时间[38]相关,建议CDCL解决者利用社区结构。More precisely, they target variables linking distinct communities, possibly as a way to solve by divide-and-conquer approach.译文:更准确地说,它们以连接不同社区的变量为目标,这可能是一种分而治之的方法。 |
|
|
In the VSIDS vs. TGC experiments (Sect. 4), we used the Spearman’s rank correlation coefficient to show that the VSIDS and TGC rankings are strongly correlated. From our experiments, we can say that for all the VSIDS variants considered in this paper, additive bumping matches with the increase in centrality of the chosen variables. We also observe from our results that the variables that solvers pick for branching have very high TGC rank. The concept of centrality allows us to define in a mathematically precise the intuition many solver developers have had, i.e., that branching on “highly constrained variables” is an effective strategy.译文:中心性的概念允许我们在数学上精确地定义许多求解器开发人员的直觉,即“高度约束变量”分支是一种有效的策略。 Our bridge variable experiment combined with the TGC experiment suggests that VSIDS focuses on high-centrality bridge variables. |
|
|
What role does multiplicative decay play in making VSIDS so effective?译文:在使VSIDS如此有效的过程中,乘法衰变起了什么作用? (Answered by Contribution IV, that in turn led to a new adaptive VSIDS presented as Contribution V.) We show that multiplicative decay is essentially a form of exponential smoothing (Sect. 5). 译文:乘法衰减本质上是指数平滑的一种形式。We add an explanation as to why this is important, namely, that exponential smoothing favors variables that persistently occur in conflicts and this is a better strategy for root-cause analysis. 译文:我们还解释了为什么这一点很重要,即指数平滑有利于那些在冲突中持续出现的变量,这是一个更好的根本原因分析策略。 We designed a new VSIDS technique, we call adaptVSIDS, based on the above results, wherein we rapidly decay the VSIDS activity if the learnt clause LBDs are large (Sect. 6). We showed that this technique is better than mVSIDS on the SAT Competition 2013 benchmark. |
|
|
Is VSIDS temporally and spatially focused? (Answered by Contribution II.) 译文:VSIDS是时间和空间集中的吗? We show that VSIDS exhibits spatial focus and temporal focus (Sect. 3), forms of locality in search. While there has been speculation among solver researchers that CDCL with VSIDS solvers perform local search, we precisely define spatial and temporal locality in terms of the community structure.译文:虽然求解器研究者推测使用VSIDS求解器的CDCL执行局部搜索,但我们根据群落结构精确地定义了空间和时间局部性。 |
|
8 Related Work
|
Marques-Silva and Sakallah are credited with inventing the CDCL technique [34].译文:马克-席尔瓦和萨卡拉被认为是CDCL技术[34]的发明者。 The original VSIDS heuristic was invented by the authors of Chaff [36]. Armin Biere [8] described the low-pass filter behavior of VSIDS, and Huang et al. [26] stated that VSIDS is essentially an EMA.译文:Huang等人[26]指出VSIDS本质上是EMA。 Katsirelos and Simon [30] were the first to publish a connection between eigenvector centrality and branching heuristics.译文:Katsirelos和Simon[30]是第一个发表特征向量中心性和分支启发式之间联系的人。 In their paper [30], the authors computed eigenvector centrality (via Google PageRank) only once on the original input clauses and showed that most of the decision variables have higher than average centrality.译文:大多数决策变量的中心性都高于平均中心性。 Also, it bears stressing that their definition of centrality is not temporal. By contrast, our results correlate VSIDS ranking with temporal degree and eigenvector centrality, and show the correlation holds dynamically throughout the run of the solver.译文:我们的结果将VSIDS排序与时间程度和特征向量中心性关联起来,并表明这种关联在求解器运行过程中是动态存在的。 Also, we noticed that the correlation is also significantly stronger after extending centrality with temporality. 译文:我们注意到,随着时间的延长中心性后,相关性也显著增强。 Simon and Katsirelos do hypothesize that VSIDS may be picking bridge variables (they call them fringe variables). However, they do not provide experimental evidence for this. To the best of our knowledge, we are the first to establish the following results regarding VSIDS:译文:据我们所知,我们是第一个建立关于VSIDS的以下结果的:
|
|
9 Conclusions and Future Work
|
In this paper we present various empirically-verified findings on VSIDS.译文:在本文中,我们提出了VSIDS的各种经验验证的发现。 We show that VSIDS tends to favor the high-centrality bridge variables in the community structure of the Boolean formula. In addition, we show that VSIDS focuses on a small subset of communities in the graph of a SAT instance during search. Lastly, we explain the multiplicative decay of VSIDS with EMA and use this finding to devise a new branching heuristic we call adaptVSIDS.译文:我们用EMA解释了VSIDS的乘法衰减,并利用这一发现设计了一个新的分支启发式,我们称之为adaptVSIDS。 These results put together show that community structure, graph centrality, and exponential smoothing are important lenses through which to understand the behavior of the VSIDS family of branching heuristics and CDCL SAT solving.译文:这些结果放在一起表明,社区结构、图的中心性和指数平滑是理解分支启发式和CDCL SAT求解VSIDS家族行为的重要透镜。
In the future, we plan to strengthen our results by considering a larger number of benchmarks, solvers, branching heuristics, and graph representations.译文:在未来,我们计划通过考虑更多的基准、求解器、分支启发式和图表示来增强我们的结果。 |
|
Footnotes
| 1.
All code and experimental data sets are available from our website: https://github.com/JLiangWaterloo/vsids. |
|
| 2.
MiniSAT’s actual implementation is slightly different, but has the same effect. Rather than decaying the activities of every variable, it increases the bump quantum of all future conflicts instead [8]. |
References
-
Starexec. http://www.starexec.org/
-
2.Proceedings of Past SAT Conferences (2013). http://www.satisfiability.org
-
3.SAT Competition Website (2013). http://www.satcompetition.org
-
4.SHARCNET Website (2013). https://www.sharcnet.ca
-
5.Atserias, A., Fichte, J.K., Thurley, M.: Clause-learning algorithms with many restarts and bounded-width resolution. In: Kullmann, O. (ed.) SAT 2009. LNCS, vol. 5584, pp. 114–127. Springer, Heidelberg (2009)CrossRefGoogle Scholar
-
6.Audemard, G., Simon, L.: Glucose: a solver that predicts learnt clauses quality. IJCAI 9, 399–404 (2009)Google Scholar
-
7.Beame, P., Kautz, H.A., Sabharwal, A.: Towards understanding and harnessing the potential of clause learning. J. Artif. Intell. Res. (JAIR) 22, 319–351 (2004)MathSciNetzbMATHGoogle Scholar
-
8.Biere, A.: Adaptive restart strategies for conflict driven SAT solvers. In: Kleine Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 28–33. Springer, Heidelberg (2008)CrossRefGoogle Scholar
-
9.Biere, A.: Lingeling (2010)Google Scholar
-
10.Blondel, V.D., Guillaume, J.L., Lambiotte, R., Lefebvre, E.: Fast unfolding of communities in large networks. J. Stat. Mech. Theor. Exp. 2008(10), P10008 (2008)CrossRefGoogle Scholar
-
11.Brown, R.G.: Exponential Smoothing for Predicting Demand. Little, Cambridge (1956)Google Scholar
-
12.Buro, M., Büning, H.K.: Report on a SAT competition. Fachbereich Math.-Informatik, Univ. Gesamthochschule (1992)Google Scholar
-
13.Clauset, A., Newman, M.E., Moore, C.: Finding community structure in very large networks. Phys. Rev. E 70(6), 066111 (2004)CrossRefGoogle Scholar
-
14.Cook, S.A.: The complexity of theorem-proving procedures. In: Proceedings of the Third Annual ACM Symposium on Theory of Computing, STOC 1971, pp. 151–158. ACM, New York (1971)Google Scholar
-
15.Een, N., Sörensson, N.: MiniSat: a SAT solver with conflict-clause minimization. In: SAT 2005 (2005)Google Scholar
-
16.Faust, K.: Centrality in affiliation networks. Soc. Netw. 19(2), 157–191 (1997)CrossRefGoogle Scholar
-
17.Fisher, R.A.: Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika 10(4), 507–521 (1915)Google Scholar
-
18.Freeman, J.W.: Improvements to propositional satisfiability search algorithms. Ph.D. thesis, Philadelphia, PA, USA (1995). uMI Order No. GAX95-32175Google Scholar
-
19.Freeman, L.: Centrality in social networks conceptual clarification. Soc. Netw. 1(3), 215–239 (1979)CrossRefGoogle Scholar
-
20.Gini, C.: Measurement of inequality of incomes. Econ. J. 31(121), 124–126 (1921)CrossRefGoogle Scholar
-
21.Girvan, M., Newman, M.E.: Community structure in social and biological networks. Proc. Natl. Acad. Sci. 99(12), 7821–7826 (2002)MathSciNetCrossRefzbMATHGoogle Scholar
-
22.Gloor, P., Krauss, J., Nann, S., Fischbach, K., Schoder, D.: Web science 2.0: identifying trends through semantic social network analysis. In: 2009 International Conference on Computational Science and Engineering, CSE 2009, vol. 4, pp. 215–222, August 2009Google Scholar
-
23.Golub, G.H., Van Loan, C.F.: Matrix Computations. JHU Press, Baltimore (2012)zbMATHGoogle Scholar
-
24.Hamadi, Y., Jabbour, S., Sais, L.: ManySAT: a parallel SAT solver. JSAT 6(4), 245–262 (2009)zbMATHGoogle Scholar
-
25.Hoos, H.H., Stützle, T.: Stochastic Local Search: Foundations & Applications. Morgan Kaufmann Publishers Inc., San Francisco (2004)zbMATHGoogle Scholar
-
26.Huang, R., Chen, Y., Zhang, W.: SAS+ planning as satisfiability. J. Artif. Int. Res. 43(1), 293–328 (2012)MathSciNetzbMATHGoogle Scholar
-
27.Iser, M., Taghdiri, M., Sinz, C.: Optimizing MiniSAT variable orderings for the relational model finder kodkod. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 483–484. Springer, Heidelberg (2012)CrossRefGoogle Scholar
-
28.Jeroslow, R.G., Wang, J.: Solving propositional satisfiability problems. Ann. Math. Artif. Intell. 1(1–4), 167–187 (1990)CrossRefzbMATHGoogle Scholar
-
29.Katebi, H., Sakallah, K.A., Marques-Silva, J.P.: Empirical study of the anatomy of modern SAT solvers. In: Sakallah, K.A., Simon, L. (eds.) SAT 2011. LNCS, vol. 6695, pp. 343–356. Springer, Heidelberg (2011)CrossRefGoogle Scholar
-
30.Katsirelos, G., Simon, L.: Eigenvector centrality in industrial SAT instances. In: Milano, M. (ed.) CP 2012. LNCS, vol. 7514, pp. 348–356. Springer, Heidelberg (2012)CrossRefGoogle Scholar
-
31.Kaufman, P.J.: Trading Systems and Methods. Wiley, New York (2013)Google Scholar
-
32.Mahajan, Y.S., Fu, Z., Malik, S.: Zchaff2004: an efficient SAT solver. In: H. Hoos, H., Mitchell, D.G. (eds.) SAT 2004. LNCS, vol. 3542, pp. 360–375. Springer, Heidelberg (2005)CrossRefGoogle Scholar
-
33.Marques-Silva, J.: The impact of branching heuristics in propositional satisfiability algorithms. In: Barahona, P., Alferes, J.J. (eds.) EPIA 1999. LNCS (LNAI), vol. 1695, pp. 62–74. Springer, Heidelberg (1999)CrossRefGoogle Scholar
-
34.Marques-Silva, J.P., Sakallah, K.A.: Grasp: a search algorithm for propositional satisfiability. IEEE Trans. Comput. 48(5), 506–521 (1999)MathSciNetCrossRefGoogle Scholar
-
35.Moskewicz, M.W., Madigan, C.F., Malik, S.: Method and system for efficient implementation of boolean satisfiability (26 August 2008), US Patent 7,418,369Google Scholar
-
36.Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: engineering an efficient SAT solver. In: Proceedings of the 38th Annual Design Automation Conference, DAC 2001, pp. 530–535. ACM, New York (2001)Google Scholar
-
37.Nadel, A., Ryvchin, V.: Assignment stack shrinking. In: Strichman, O., Szeider, S. (eds.) SAT 2010. LNCS, vol. 6175, pp. 375–381. Springer, Heidelberg (2010)CrossRefGoogle Scholar
-
38.Newsham, Z., Ganesh, V., Fischmeister, S., Audemard, G., Simon, L.: Impact of community structure on SAT solver performance. In: Sinz, C., Egly, U. (eds.) SAT 2014. LNCS, vol. 8561, pp. 252–268. Springer, Heidelberg (2014)Google Scholar
-
39.Pipatsrisawat, K., Darwiche, A.: On the power of clause-learning SAT solvers with restarts. In: Gent, I.P. (ed.) CP 2009. LNCS, vol. 5732, pp. 654–668. Springer, Heidelberg (2009)CrossRefGoogle Scholar
-
40.Spearman, C.: The proof and measurement of association between two things. Am. J. Psychol. 15(1), 72–101 (1904)CrossRefGoogle Scholar
-
41.Straffin, P.D.: Linear algebra in geography: eigenvectors of networks. Math. Mag. 53(5), 269–276 (1980)MathSciNetCrossRefzbMATHGoogle Scholar
-
42.Yu, P.S., Li, X., Liu, B.: Adding the temporal dimension to search - a case study in publication search. In: Skowron, A., Agrawal, R., Luck, M., Yamaguchi, T., Morizet-Mahoudeaux, P., Liu, J., Zhong, N. (eds.) Web Intelligence, pp. 543–549. IEEE Computer Society (2005)Google Scholar
-
43.Zhang, W., Pan, G., Wu, Z., Li, S.: Online community detection for large complex networks. In: Proceedings of the Twenty-Third international joint conference on Artificial Intelligence, pp. 1903–1909. AAAI Press (2013)Google Scholar
核心代码解读:
(感谢文献作者提供了代码供学习和思考)
初始化数据成员如下: |
|
1 /*_________________________________________________________________________________________________ 2 | 3 | search : (nof_conflicts : int) (params : const SearchParams&) -> [lbool] 4 | 5 | Description: 6 | Search for a model the specified number of conflicts. 7 | NOTE! Use negative value for 'nof_conflicts' indicate infinity. 8 | 9 | Output: 10 | 'l_True' if a partial assigment that is consistent with respect to the clauseset is found. If 11 | all variables are decision variables, this means that the clause set is satisfiable. 'l_False' 12 | if the clause set is unsatisfiable. 'l_Undef' if the bound on number of conflicts is reached. 13 |________________________________________________________________________________________________@*/ 14 lbool Solver::search(int nof_conflicts) 15 { 16 assert(ok); 17 int backtrack_level; 18 int conflictC = 0; 19 vec<Lit> learnt_clause; 20 starts++; 21 22 for (;;){ 23 CRef confl = propagate(); 24 if (confl != CRef_Undef){ 25 // CONFLICT 26 conflicts++; conflictC++; 27 if (decisionLevel() == 0) return l_False; 28 29 learnt_clause.clear(); 30 analyze(confl, learnt_clause, backtrack_level); 31 backjumps += decisionLevel() - backtrack_level; 32 cancelUntil(backtrack_level); 33 34 if (learnt_clause.size() == 1){ 35 uncheckedEnqueue(learnt_clause[0]); 36 }else{ 37 CRef cr = ca.alloc(learnt_clause, true); 38 learnts.push(cr); 39 attachClause(cr); 40 claBumpActivity(ca[cr]); 41 uncheckedEnqueue(learnt_clause[0], cr); 42 } 43 44 int lbd_val = lbd(learnt_clause); 45 lbd_ema = lbd_ema_decay * lbd_ema + (1 - lbd_ema_decay) * lbd_val; //移动平均线上的取值lbd_ema 46 if (lbd_val >= lbd_ema) { //当前学习子句的LBD大于均线值,使用较小的衰减因子,大的增量间隔。 47 decays++; 48 varDecayActivity(var_decay); //增量系数为前一次的(1/0.85)倍,代码为var_inc *= (1 / 0.85) 49 } else { 50 thresh_decays++; 51 varDecayActivity(var_thresh_decay); //增量系数为原来的 52 } 53 claDecayActivity(); 54 55 if (--learntsize_adjust_cnt == 0){ 56 learntsize_adjust_confl *= learntsize_adjust_inc; 57 learntsize_adjust_cnt = (int)learntsize_adjust_confl; 58 max_learnts *= learntsize_inc; 59 60 if (verbosity >= 1) 61 printf("| %9d | %7d %8d %8d | %8d %8d %6.0f | %6.3f %% |\n", 62 (int)conflicts, 63 (int)dec_vars - (trail_lim.size() == 0 ? trail.size() : trail_lim[0]), nClauses(), (int)clauses_literals, 64 (int)max_learnts, nLearnts(), (double)learnts_literals/nLearnts(), progressEstimate()*100); 65 } 66 67 }else{ 68 // NO CONFLICT 69 if (nof_conflicts >= 0 && conflictC >= nof_conflicts || !withinBudget()){ 70 // Reached bound on number of conflicts: 71 progress_estimate = progressEstimate(); 72 cancelUntil(0); 73 return l_Undef; } 74 75 // Simplify the set of problem clauses: 76 if (decisionLevel() == 0 && !simplify()) 77 return l_False; 78 79 if (learnts.size()-nAssigns() >= max_learnts) 80 // Reduce the set of learnt clauses: 81 reduceDB(); 82 83 Lit next = lit_Undef; 84 while (decisionLevel() < assumptions.size()){ 85 // Perform user provided assumption: 86 Lit p = assumptions[decisionLevel()]; 87 if (value(p) == l_True){ 88 // Dummy decision level: 89 newDecisionLevel(); 90 }else if (value(p) == l_False){ 91 analyzeFinal(~p, conflict); 92 return l_False; 93 }else{ 94 next = p; 95 break; 96 } 97 } 98 99 if (next == lit_Undef){ 100 // New variable decision: 101 decisions++; 102 next = pickBranchLit(); 103 104 if (next == lit_Undef) 105 // Model found: 106 return l_True; 107 } 108 109 // Increase decision level and enqueue 'next' 110 newDecisionLevel(); 111 uncheckedEnqueue(next); 112 } 113 } 114 } |
|
| 注意: 增量间距的修改体现在下一次决策——BCP——冲突生成和冲突分析阶段。 |



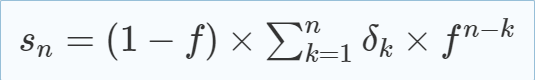

 浙公网安备 33010602011771号
浙公网安备 33010602011771号