01背包-动态分配问题简述

最近遇到一道题，解题过程让我豁然开朗，在他人的题解和分析中找到了这个问题的解法，于是记录这个思想破壳过程，希望对大家有用。

01背包是动态规划问题，你不必一定要输出限制死的结果，而是要输出满足条件的最优解。例如下面这道题

题目描述

      辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。” 
如果你是辰辰，你能完成这个任务吗？

 

       在这道题里面我们可以看到，每个时间和价值都知道，然后给定规定的时间，在这期间，如我们需要让采集的草药价值最大，那就需要有取舍。

在还没接触这个算法之前，我认为要想得到想要结果，那就需要先按价值排序，然后取一个，再取一个，一步步比较，直到之后的结果最大，可这样做的结果就是，太繁琐。

       而这个算法，却不是取一个比较，再取两个比较那样，而是将物品选择拿或者不拿。例如在拿了A草药时，规定的时间将变小，而在这个规定时间里再选除此之外的其它药物，如果不拿，规定时间不变，再在这个时间内拿其它草药。最后再两个方法得到的价值进行比较得出最后的结果。但我们也不必一定是要一开始就在给定的时间里寻找，我们可以缩小草药数量，缩短采取时间，再加一步得到想要的到的结果。于是有下面这个公式：

sumvalue[ m ] [ t ]=max {  sumvalue[ m-1 ]  [ t-time[m] ]  +  value[ m ]   ，sumvalue[ m-1 ]  [ t ]  }  ；

其中m代表草药数量（非已经采入），t代表给的多长时间，

在这里我们给草药编号，例如草药A,B,C时间与价值分别为(2,3)，(4,5)，(1,4)，记录成以下列表：

	time	value	0	1	2	3	4	5
A  0	2	3	0	0	3	3	3	3
B  1	4	5	0	0	3	3	5	5
C  2	1	4	0	4	4	7	7	9

 

在这里我们将草药看做行，将时间看做列，得出sumvalue[ m ] [ t ]数组表格，其中标红的九就是我们最后得到的结果。我们适当分析该表是如何得到的。

       当只有草药A的时候，我们只需要时间大于等于2，就可以采集，于是表格从第1行第2列开始就是采集到价值3的草药，此时我们得到的数据都是最优解，并且我们将数据记录在二维数组里。

当只有草药A，B的时候呢？此时我们就要考虑要不要采集草药B的了（此时我们是从B草药开始第一采集），首先我们要判断此时采草药时间是否足够，如果不足够的话，那情况就和只有草药A，并且时间相同的情况一样了，即sumvalue[m][t] = sumvalue[m-1][t];如果足够的话，那我们就采集了，那相应的数量和时间减少，价值加上B的价值，再在这个基础上判断A草药是否加入，而A草药是否加入在上一列已经做出选择，我们将两次的价值进行相加，然后再与未加入B草药时的价值（时间一致，草药数量降低一个，而这个时间段，草药数量恰好在上一行）进行比较得出此时该数量，该时间的最优解，即公式sumvalue[ m ] [ t ]=max {  sumvalue[ m-1 ]  [ t-time[m] ]  +  value[ m ]   ，sumvalue[ m-1 ]  [ t ]  } 

例如时间4, 草药有A，B时，有sumvalue[1][4] = max {  sumvalue[ 0 ]  [0]  +  value[ 1 ]   ，sumvalue[ 0 ]  [4 ]  } ，此时sumvalue[ 0 ]  [0]的价值最优（即只有草药A和只有0个时间）在上一行已经得出，再与没有草药B时该时间里的最优解比较，得出该时间和该草药数量时的最优解max{0+5，3}=5，如下图所示：

   

 

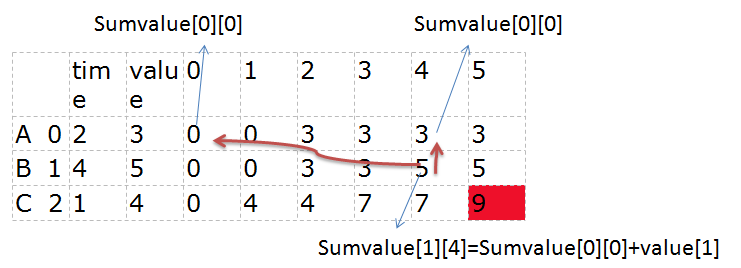
       在这个图可以很清晰的看出来，一步有两个选择方向，红色线为选择方向，一步步回溯，最终得到最优解（但我们这里是递推，前面求的解已经存入数组里）。

时间4，草药有A，B，C时，有sumvalue[2][4] = max {  sumvalue[ 1 ]  [3]  +  value[ 2 ]   ，sumvalue[ 1 ]  [4 ]  }，sumvalue[1][4]上面刚求出，该公式就

等于sumvalue[2][4] = max{3+4,5}=7;该选择结构如下：

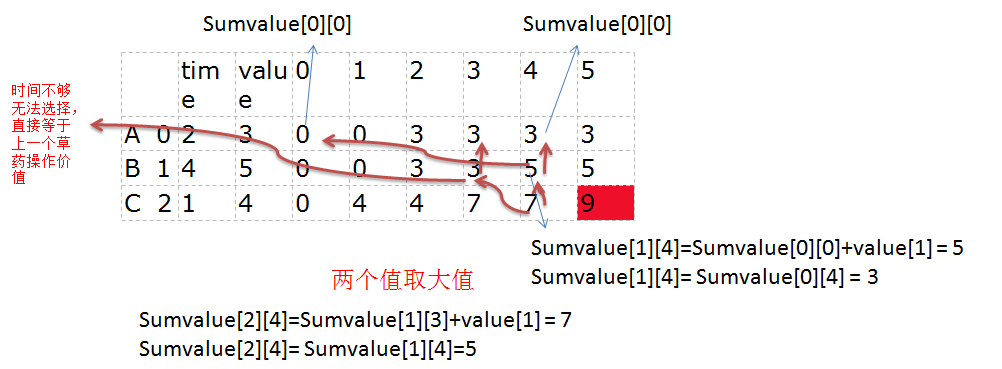
我想看到这应该大致就能了解这个动态规划的大致过程了，在编程里我们只需要按照草药数量逐个加一，时间逐一相加最后得到在某个草药数量，某个时间段的最优解。

 

下面是原始题的输入输出：

输入

输入第一行有两个整数T（1 <= T <= 1000）和M（1 <= M <= 100），用一个空格隔开，T代表总共能够用来采药的时间，M代表山洞里的草药的数目。接下来的M行每行包括两个在1到100之间（包括1和100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出

输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例输入

70 3
71 100
69 1
1 2

样例输出

3
代码如下：

#include "stdio.h"
#include "string.h"

int max(int i,int j)
{
    if(i<j) return j;
    else return i;
}
int main()
{
    int T,M,j;
    int i=0;
    int time[100];//草药数量
    int value[100];//草药时间
    int total[100][1001];
    scanf("%d%d",&T,&M);

    for(i=0; i<M; i++)
    {
        scanf("%d%d",&time[i],&value[i]);
    }
    for(i=0; i<M; i++)//M个草药
    {
         for(j=0; j<=T ;j++)//T+1时间，包括0时间
        {
            if(i==0)
            {
                if(time[i]<=j) total[i][j]=value[i];
                else total[i][j] = 0;
            }
            else
            {
                if(time[i]<=j) total[i][j] = max(total[i-1][j-time[i]]+value[i],total[i-1][j]);
                else total[i][j] = total[i-1][j];
            }
        }
    }
    printf("%d",total[M-1][T]);
    return 0;
}