排序算法复杂度

      1、排序算法基础

1. 1. 排序算法，是一种能将一串数据按照特定的排序方式进行排列的一种算法，一个排序算法的好坏，主要从时间复杂度，空间复杂度，稳定性来衡量。
   2. 评价排序算法优劣的标准主要是两条：一是算法的运算量，这主要是通过记录的比较次数和移动次数来反应；另一个是执行算法所需要的附加存储单元的的多少。

      2、内部排序与外部排序

1. 1. 根据排序过程中，待排序的数据是否全部被放在内存中，分为两大类：
   2. 内部排序：指的是待排序的数据存放在计算机内存中进行的排序过程；
   3. 外部排序：指的是排序中要对外存储器进行访问的排序过程。

      3、时间复杂度

1. 1. 时间复杂度是一个函数，语句总的执行次数与问题规模n的函数表达式，它描述了该算法的运行时间，考察的是当输入值大小趋近无穷时的情况。数学和计算机科学中使用这个大 O 符号用来标记不同”阶“的无穷大。这里的无穷被认为是一个超越边界而增加的概念，而不是一个数。
   2. 想了解时间复杂度，常见的 O(1)，O(log n)，O(n)，O(n log n)，O(n^2) ，计算时间复杂度的过程，常常需要分析一个算法运行过程中需要的基本操作，计量所有操作的数量。
   3. 时间是累积的，但是空间不是累积的，可重复使用。
   4. 冒泡、选择、插入、归并、希尔、堆排序都是基于比较的排序，平均时间复杂度最低O(nlogn)；

      4、O（1）常数阶

1. 1. O（1）中的 1 并不是指时间为 1，也不是操作数量为 1，而是表示操作次数为一个常数，不因为输入 n 的大小而改变，比如哈希表里存放 1000 个数据或者 10000 个数据，通过哈希码查找数据时所需要的操作次数都是一样的，而操作次数和时间是成线性关系的，所以时间复杂度为 O（1）的算法所消耗的时间为常数时间。

      5、O（log n）对数阶

1. 1. O（log n）中的 log n 是一种简写，loga n 称作为以 a 为底 n 的对数，log n 省略掉了 a，所以 log n 可能是 log2 n，也可能是 log10 n。但不论对数的底是多少，O（log n）是对数时间算法的标准记法，对数时间是非常有效率的，例如有序数组中的二分查找，假设 1000 个数据查找需要 1 单位的时间， 1000,000 个数据查找则只需要 2 个单位的时间，数据量平方了但时间只不过是翻倍了。如果一个算法他实际的得操作数是 log2 n + 1000， 那它的时间复杂度依旧是 log n， 而不是 log n + 1000，时间复杂度可被称为是渐近时间复杂度，在 n 极大的情况，1000 相对 与 log2 n 是极小的，所以 log2 n + 1000 与 log2 n 渐进等价。

      6、O（n）线性阶

1. 1. 如果一个算法的时间复杂度为 O(n)，则称这个算法具有线性时间，或 O(n) 时间。这意味着对于足够大的输入，运行时间增加的大小与输入成线性关系。例如，一个计算列表所有元素的和的程序，需要的时间与列表的长度成正比。遍历无序数组寻最大数，所需要的时间也与列表的长度成正比。

      7、O（n log n）线性对数阶

1. 1. 排序算法中的快速排序的时间复杂度即 O（n log n），它通过递归 log2n 次，每次遍历所有元素，所以总的时间复杂度则为二者之积， 复杂度既 O（n log n）。

      8、O（n^2）平方阶

1. 1. 冒泡排序的时间复杂度既为 O（n^2），它通过平均时间复杂度为 O（n）的算法找到数组中最小的数放置在争取的位置，而它需要寻找 n 次，不难理解它的时间复杂度为 O（n^2）。时间复杂度为 O（n^2）的算法在处理大数据时，是非常耗时的算法，例如处理 1000 个数据的时间为 1 个单位的时间，那么 1000,000 数据的处理时间既大约 1000,000 个单位的时间。
   2. 时间复杂度又有最优时间复杂度，最差时间复杂度，平均时间复杂度。部分算法在对不同的数据进行操作的时候，会有不同的时间消耗，如快速排序，最好的情况是 O（n log n），最差的情况是 O（n²），而平均复杂度就是所有情况的平均值。

      9、时间复杂度效率比较

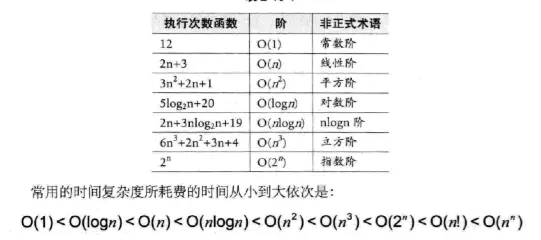
1. 1. 除了上述所说的时间复杂度，下表中展示了其他一些时间复杂度，以及这些时间复杂度之间的比较。想O(n^3)、O(n!)等这样的时间复杂度，过大的n会使算法变得不现实，都是时间的噩梦，所以这种不切实际的复杂度，一般都不会去考虑这样的算法。

      10、空间复杂度

1. 1. 和时间复杂度一样，有 O(1)，O(log n)，O(n)，O(n log n)，O(n^2)，等等。实际写代码的过程中完全可以用空间来换取时间。比如判断2017年之前的某一年是不是闰年，通常可以通过一个算法来解决。但还有另外一种做法就是将2017年之前的闰年保存到一个数组中。如果某一年存在这个数组中就是闰年，反之就不是。一般来说时间复杂度和空间复杂度是矛盾的。到底优先考虑时间复杂度还是空间复杂度，取决于实际的应用场景。

      11、原地算法

1. 1. 不依赖额外的资源或者依赖少数的额外资源，仅依靠输出来覆盖输入，空间复杂度为 O(1) 的都可以认为是原地算法 In-place；
   2. 桶排序属于非原地算法，称为 Not-in-place 或者 Out-of-place；

       12、稳定性

1. 1. 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri = rj，且 ri 在 rj 之前，而在排序后的序列中，ri 仍在 rj 之前，则称这种排序算法是稳定的；否则称为不稳定的。
   2. 当相等的元素是无法分辨的，比如像是整数，稳定性并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

      (4, 1)  (3, 1)  (3, 7) （5, 6）

   3. 在这个状况下，有可能产生两种不同的结果，一个是让相等键值的纪录维持相对的次序，而另外一个则没有：

      (3, 1)  (3, 7)  (4, 1)  (5, 6)  （维持次序）
      (3, 7)  (3, 1)  (4, 1)  (5, 6)  （次序被改变）

   4. 不稳定排序算法可能会在相等的键值中改变纪录的相对次序，这导致我们无法准确预料排序结果（除非你把数据在你的大脑里用该算法跑一遍），但是稳定排序算法从来不会如此。例如冒泡排序即稳定的存在，相等不交换则不打乱原有顺序。而快速排序有时候则是不稳定的。

---

参考资料：

• https://www.jianshu.com/p/2496f7be35d3
• https://www.jianshu.com/p/4b409422c678
• https://blog.csdn.net/hansionz/article/details/81781918
• http://www.cocoachina.com/articles/181910