归并排序

一、原理

       ☆思想：归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，类似二叉树两个子节点中的序列有序，合并到父节点，仍然有序；该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，作为一种典型的分而治之思想的算法应用，归并排序的实现有两种方法：

  • 自上而下的递归
  • 自下而上的迭代

       ☆过程：以递增为例，用数组表示，长度为n，分别用递归和迭代实现，这两部分都用到了归并过程，输入两个有序序列，同时遍历，比较，小的先归入，如果有一个序列已全部归入，另一个序列其余元素顺序归入；

  • 找到数组中间位置，拆分为左右两部分，这两部分如果长度大于1，递归拆分，返回归并结果；
  • 定义初始间隔为1，即每两个相邻元素归并，如果输入序列为偶数个，则刚好两两合并，如果为奇数个，最后一个元素不处理；间隔加倍，即刚归并的两个相邻元素与紧接着的两个相邻元素归并，如果最后剩余三个元素，则把前两个和最后一个看成两部分合并；……不断加倍间隔，直到大于输入序列长度，此时输入序列有序；

二、实现代码

      JavaScript 代码递归实现

function mergeSort(arr) {

   return split(arr, 0, arr.length - 1);

}

function split(arr, s, e) {
    var mid;
    var left = [],
    right = [];

    //将数组拆分为左右两个集合；
    mid = s + Math.floor((e - s) / 2);

    if (mid > s) {
        left = split(arr.slice(s, mid + 1), 0, mid - s);

    } else {
        left = arr.slice(s, mid + 1);
    }

    if (e - mid > 1) {
        right = split(arr.slice(mid + 1, e + 1), 0, e - mid - 1);

    } else {
        right = arr.slice(mid + 1, e + 1);
    }

    return gb(left, right);
}

function gb(arra, arrb) {
    var arr = [];
    var i = 0,
    j = 0,
    k = 0;
    //归并插入新数组
    while (i < arra.length && j < arrb.length) {
        if (arra[i] <= arrb[j]) {
            arr[k++] = arra[i++];
        } else {
            arr[k++] = arrb[j++];
        }
    }
    //如一数组已全部插入新数组，把另一数组剩余元素插入新数组
    while (i < arra.length) {
        arr[k++] = arra[i++];
    }
    while (j < arrb.length) {
        arr[k++] = arrb[j++];
    }
    return arr;
}

 

      JavaScript 代码迭代实现

function mergeSort(arr) {
    //中间数组
    var brr = [];
    //相邻待合并元素间隔
    var n = 1;

    //合并间隔不能大于数组长度
    while (n < arr.length) {
        for (var i = 0; i < arr.length; i = i + 2 * n) {
            //根据待合并元素个数判断处理
            //可以分为两个完整分支
            if (i + 2 * n - 1 < arr.length) {
                brr = gb(arr.slice(i, i + n), arr.slice(i + n, i + 2 * n));
            } else if (i + n > arr.length - 1) { //只有一个分支，不处理
                break;
            } else { //可以分为两个分支，但第二个分支长度不够 
                brr = gb(arr.slice(i, i + n), arr.slice(i + n, arr.length));
            }

            //归并后数组复制到原数组
            for (var j = i; j < i + 2 * n && j < arr.length; j++) {
                arr[j] = brr[j - i];
            }
        }
        //每次间隔加倍
        n = 2 * n;
    }
}

function gb(arra, arrb) {
    var arr = [];
    var i = 0,
    j = 0,
    k = 0;
    //归并插入新数组
    while (i < arra.length && j < arrb.length) {
        if (arra[i] <= arrb[j]) {
            arr[k++] = arra[i++];
        } else {
            arr[k++] = arrb[j++];
        }
    }
    //如一数组已全部插入新数组，把另一数组剩余元素插入新数组
    while (i < arra.length) {
        arr[k++] = arra[i++];
    }
    while (j < arrb.length) {
        arr[k++] = arrb[j++];
    }
    return arr;
}

 

三、优化

       无；

四、复杂度

名称 时间复杂度 空间复杂度  稳定性 
平均 最坏 最优
归并排序 O(nlogn) O(nlogn) O(nlogn)  O(n) √

      递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n) ；

      

 

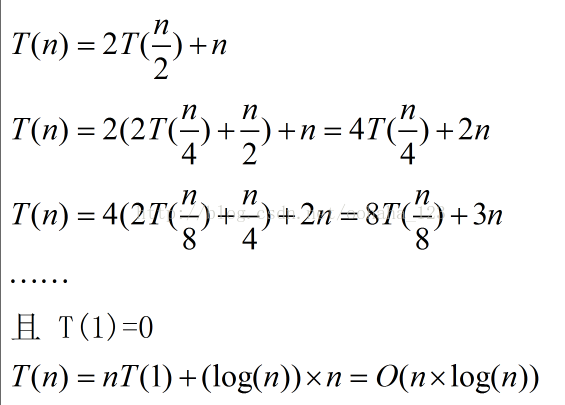
      无论原始数组是否是有序的，都要递归分隔并向上归并排序，所以时间复杂度始终是O（nlog2n）；

      迭代归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的时间复杂度是O(n*log2n)。

      每次两个数组进行归并排序的时候，都会利用一个长度为n的数组作为辅助数组用于保存合并序列，所以空间复杂度为O（n）；

      相同元素不会交换，本排序稳定。

参考资料：

posted @ 2019-11-26 12:01  老余的水壶  阅读(194)  评论(0)    收藏  举报