ADM(Diffusion Models with Analytical Image Attenuation)训练生成算法与网络结构详解
介绍
本文主要介绍论文[https://arxiv.org/abs/2306.13720](Simultaneous Image-to-Zero and Zero-to-Noise: Diffusion Models with Analytical Image Attenuation),作为一种对扩散模型的改进模型,具有生成质量更高,生成速度更快的优点。所以下面会从训练采样算法、以及backbone网络双Unet两方面介绍这篇论文提出的ADM模型。
ADM的训练方式与stable diffusion一样,先训练VAE,然后冻结VAE的参数再训练主干的双Unet网络,ADM开源项目中使用的VAE结构以及训练损失函数与stable diffusion一样,具体可参考博客:https://www.cnblogs.com/yunzhe666/p/19119433,本文不再赘述。
1.训练和采样算法
论文中日出的ADM模型与DDPM主要区别就是DDPM加噪是根据马尔可夫过程逐步加载,而ADM是将加噪分解为两部,首先使用一个解析函数将图片衰减为全0图片,然后再在全0图片上加噪。因此ADM与DDPM的前向公式、反向公式、训练时的目标函数对比如下图所示:

1.1 前向过程推导
在上图中前向公式是:
\(\mathbf{x}_t=\mathbf{x}_0+\int_0^t \mathbf{h}_t \mathrm{~d} t+\int_0^t \mathrm{~d} \mathbf{w}_t, \quad \mathbf{x}_0 \sim q\left(\mathbf{x}_0\right)\)
其中\(\mathbf{x}_0+\int_0^t \mathbf{h}_t \mathrm{~d} t\)代表图像衰减为0的过程,\(\int_0^t \mathrm{~d} \mathbf{w}_t\)代表图像加噪的过程。前向过程需要确保在t=0时\(\mathbf{x}_t \sim q\left(\mathbf{x}_0\right)\)以及在t=1时\(\mathbf{x}_t \sim \mathcal{N}\left(\mathbf{x}_1 ; \mathbf{0}, \mathbf{I}\right)\)。那么就需要\(\mathbf{x}_0+\int_0^1 \mathbf{h}_t \mathrm{~d} t=\mathbf{0}\)。由于\(\mathbf{h}_t\)是解析函数,所以我们可以用下式表示\(\mathbf{h}_t\)积分:
\(\mathbf{H}_t=\int_0^t \mathbf{h}_t \mathrm{~d} t\)
那么ADM的前向采样分布为:
\(q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \mathbf{x}_0+\mathbf{H}_t, t \mathbf{I}\right)\)
前向过程数值计算公式为:
\(\mathbf{x}_t=\mathbf{x}_0+\mathbf{H}_t+\sqrt{t} \boldsymbol{\epsilon}\)
1.2 反向过程推导:
我们可以使用后验分布\(q\left(\mathbf{x}_{t-\Delta t} \mid \mathbf{x}_t, \mathbf{x}_0\right)\)去近似\(q\left(\mathbf{x}_{t-\Delta t} \mid \mathbf{x}_t\right)\)。通过下述公式:
\(q\left(\mathbf{x}_{t-\Delta t} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\frac{q\left(\mathbf{x}_t \mid \mathbf{x}_{t-\Delta t}, \mathbf{x}_0\right) q\left(\mathbf{x}_{t-\Delta t} \mid \mathbf{x}_0\right)}{q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)}\)
可以推导出后验分布的表达式:
\(q\left(\mathbf{x}_{t-\Delta t} \mid \mathbf{x}_t, \mathbf{x}_0\right) \propto \exp \left\{-\frac{\left(\mathbf{x}_{t-\Delta t}-\widetilde{\mathbf{u}}\right)^2}{2 \widetilde{\sigma}^2 \mathbf{I}}\right\}\)
其中均值和方差分别为:
\(\widetilde{\mathbf{u}}=\mathbf{x}_t+\mathbf{H}_{t-\Delta t}-\mathbf{H}_t-\frac{\Delta t}{\sqrt{t}} \boldsymbol{\epsilon}\)
\(\widetilde{\sigma}^2=\frac{\Delta t(t-\Delta t)}{t}\)
其中方差是确定的,均值中\(\mathbf{H}_t\)和\(\boldsymbol{\epsilon}\)均由神经网络预测。
1.3 目标函数
解析函数\(\mathbf{h}_t\)的参数为\(\Phi\),所以由上面分析可知,目标函数为:
\(\min _{\boldsymbol{\theta}} \mathbb{E}_{q\left(\mathbf{x}_0\right)} \mathbb{E}_{q(\boldsymbol{\epsilon})}\left[\left\|\boldsymbol{\phi}_{\boldsymbol{\theta}}-\boldsymbol{\phi}\right\|^2+\left\|\boldsymbol{\epsilon}_{\boldsymbol{\theta}}-\boldsymbol{\epsilon}\right\|^2\right]\)
1.4 项目中的实际计算方式
解析函数\(\mathbf{h}_t\)可以为\(\mathbf{h}_t=c\)或\(\mathbf{h}_t=at+b\)或其他,但是当\(\mathbf{h}_t\)有两个或以上参数时,难以通过\(\mathbf{x}_0+\int_0^1 \mathbf{h}_t \mathrm{~d} t=\mathbf{0}\)一个等式计算所有参数,所以实际上就取\(\mathbf{h}_t=c\)。那么\(\mathbf{H}_t=ct\),\(\phi=c=-\mathbf{x}_0\)。
前向计算过程也就是:
\(\mathbf{x}_t=\mathbf{x}_0+ct+\sqrt{t} \boldsymbol{\epsilon}\)
反向过程中如果步长为s,那么计算过程为:
\(\begin{aligned}
& q\left(\mathbf{x}_{t-s} \mid \mathbf{x}_t, \mathbf{x}_0\right) \propto \exp \left\{-\frac{\left(\mathbf{x}_{t-s}-\widetilde{\mathbf{u}}\right)^2}{2 \widetilde{\sigma}^2 \mathbf{I}}\right\} \\
& \widetilde{\mathbf{u}}=\mathbf{x}_t+c(t-s)-ct-\frac{s}{\sqrt{t}} \boldsymbol{\epsilon} \\
& \widetilde{\sigma}^2=\frac{s(t-s)}{t}
\end{aligned}\)
总结下来ADM的训练和生成算法流程如下:


2.双Unet网络结构
ADM采用双Unet网络结构,原文中网络结构不够细节,这里根据项目代码绘制网络结构细节,如下图所示:
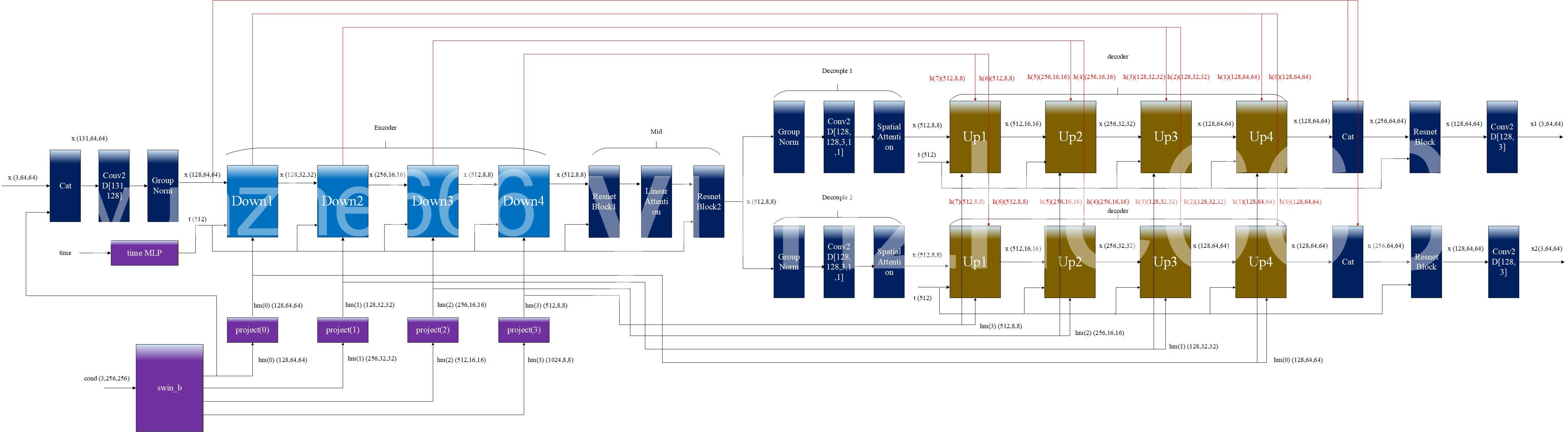
可见原文中提出的双Unet是指该网络中有一个编码器encoder,两个解码器decoder,一个mid模块,两个decouple模块,一个条件编码器以及一个时间编码器。网络中条件编码器一般使用视觉领域SOTA骨干模型swin-T,当然也可以用vgg,resnet,efficientnet代替,这里不做赘述。
下面介绍双Unet网络中各个模块设计细节:
2.1 编码器中的下采样模块(Down)
开源项目中双Unet的编码器由4个下采样模块(Down)组成,下采样模块的结构如下图所示:
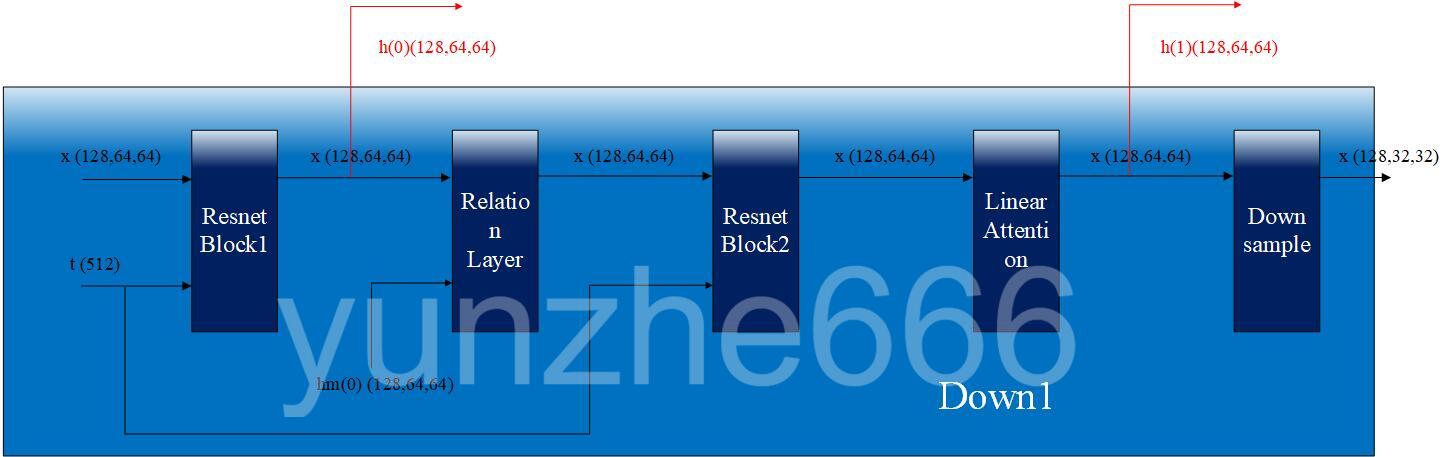
这里给出的是Down1的结构,其他下采样模块内部结构与Down1一样,只是输入张量维度大小不一样。
下采样模块中Resnet Block将时间编码向量嵌入到输入中,计算结构流程图如下图所示:
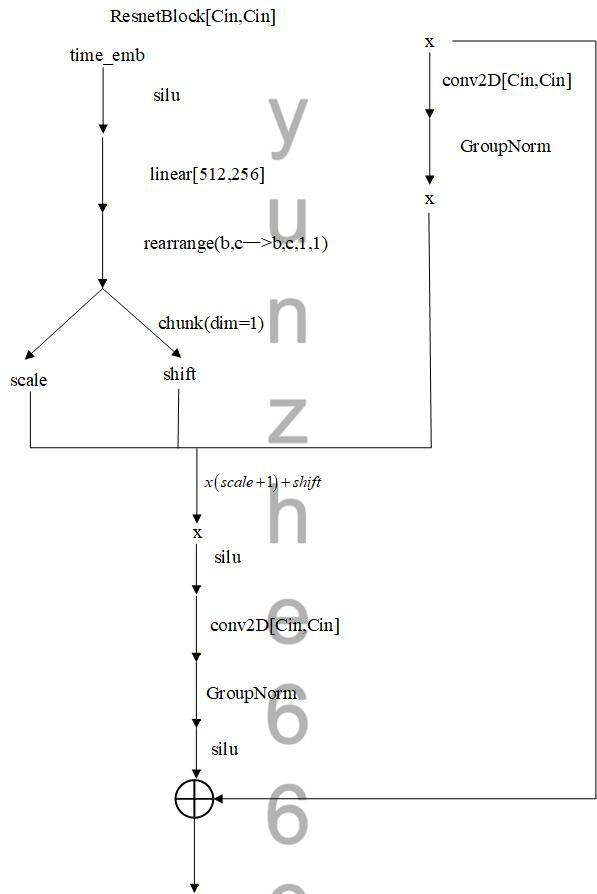
Down模块中relation layer做条件与输入的cross attention,整体结构如下:
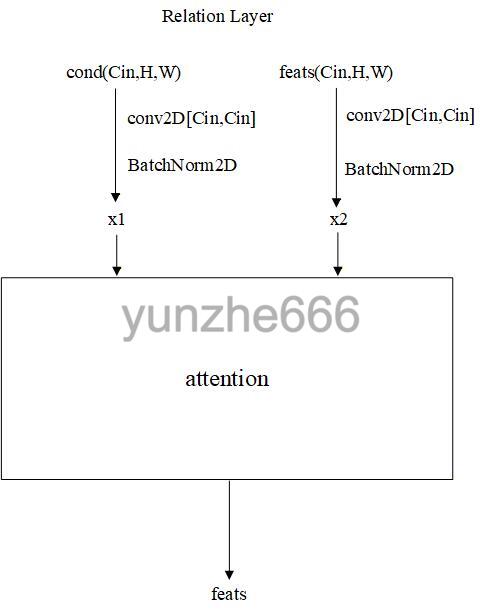
其中attention计算方式较为复杂,计算结构流程图如下:
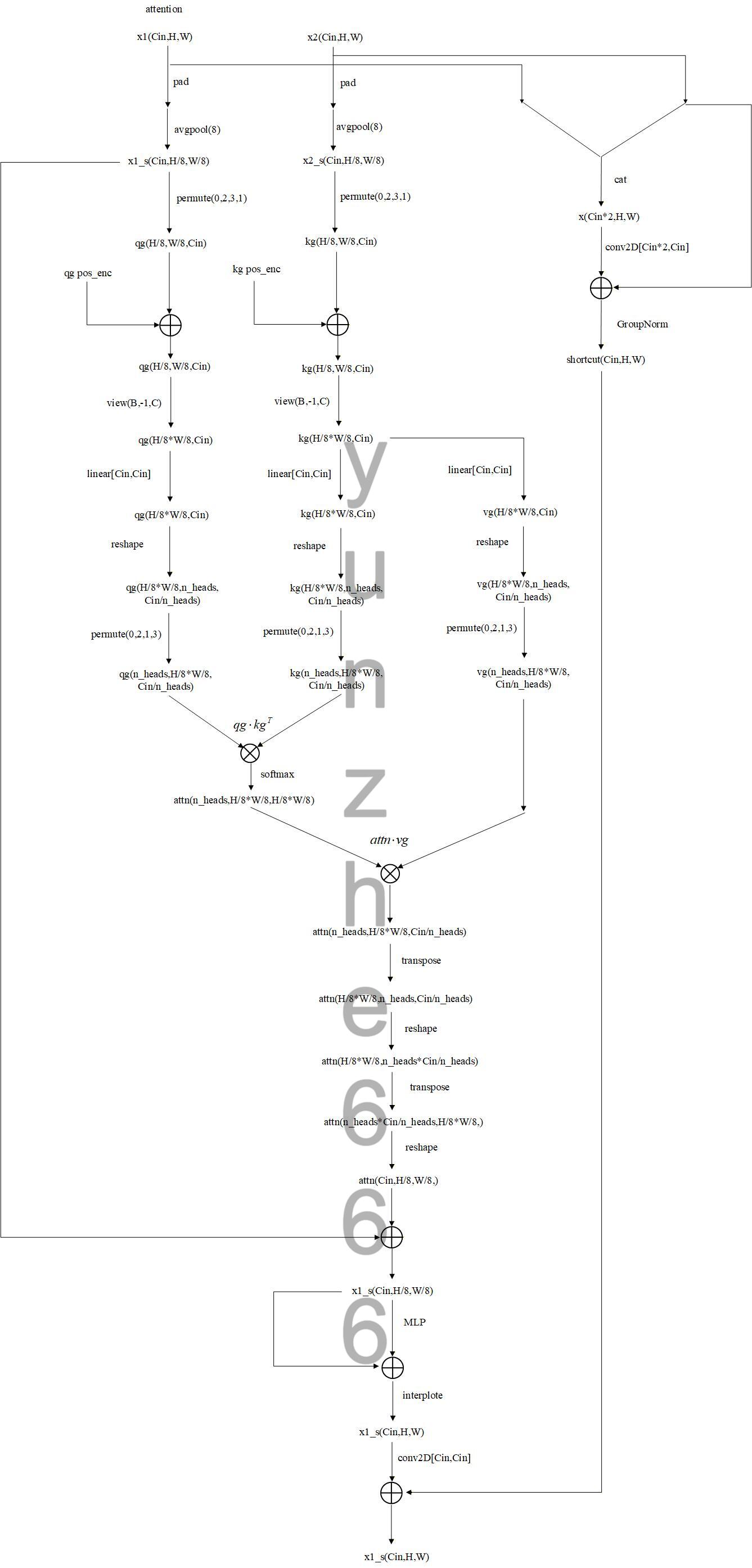
上图中的kg pos_enc和qg pos_enc代表计算kg和qg的位置编码张量,计算方法如下图:
(1)首先得到输入的x维度和y维度embedding:
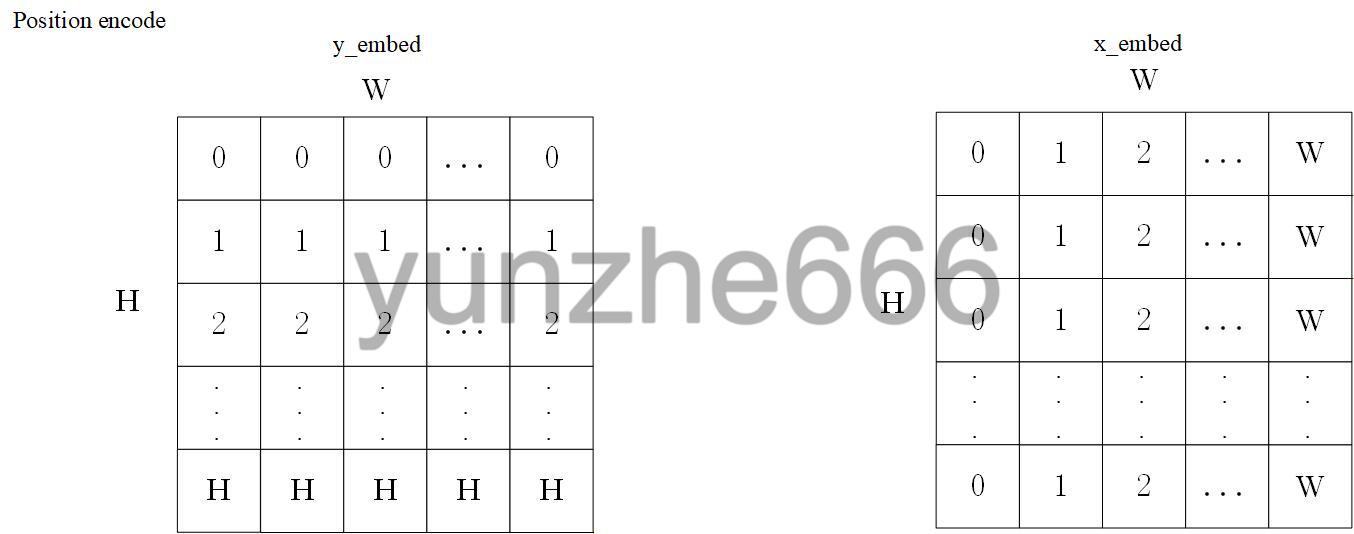
(2)然后计算x维度和y维度各自的position encode,计算方法如下图:
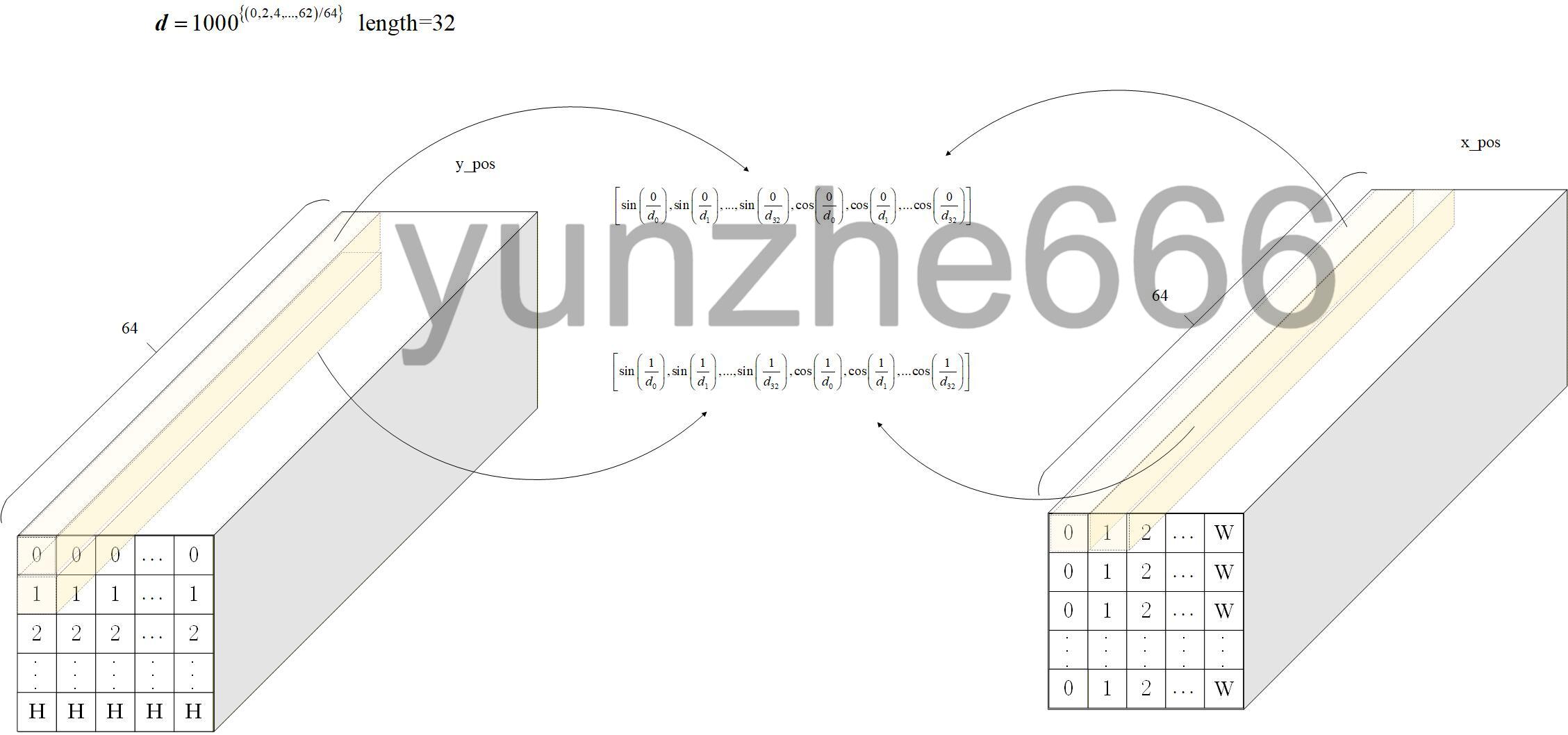
(3)最后将x维度position encode和y维度的position encode在通道维度合并,得到位置编码张量:

下采样模块中的linear attention做self-attention,使用的是线性自注意力机制,降低计算复杂度,关于linear attention原理可参考这篇博客:https://zhuanlan.zhihu.com/p/719570478。计算流程图如下图所示:
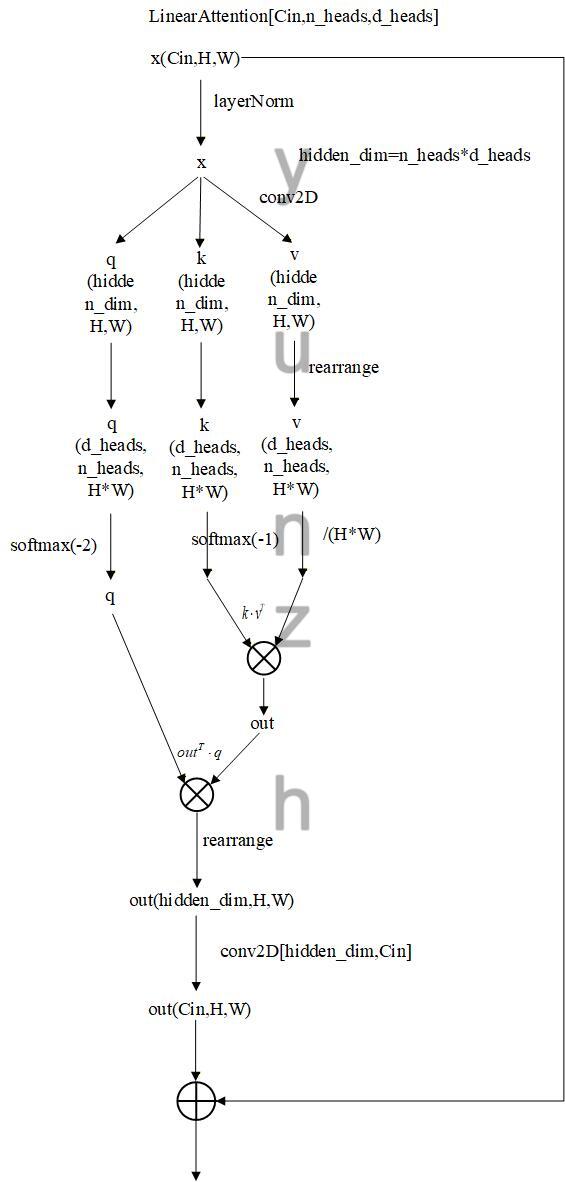
下采样模块中最后的Downsample比较简单,就是直接用一个conv2d实现H和W减半。
2.2 Mid模块
mid模块结构从双Unet网络结构可知,由Resnet Block-Linear Attention-Resnet Block组成,Resnet Block和Linear Attention结构前面由前面可知。
2.3 Decouple模块
Decouple模块结构从双Unet网络结构可知,由GroupNorm-Conv2D-Spatial Attention组成,其中Spatial Attention计算结构框图如下图所示:
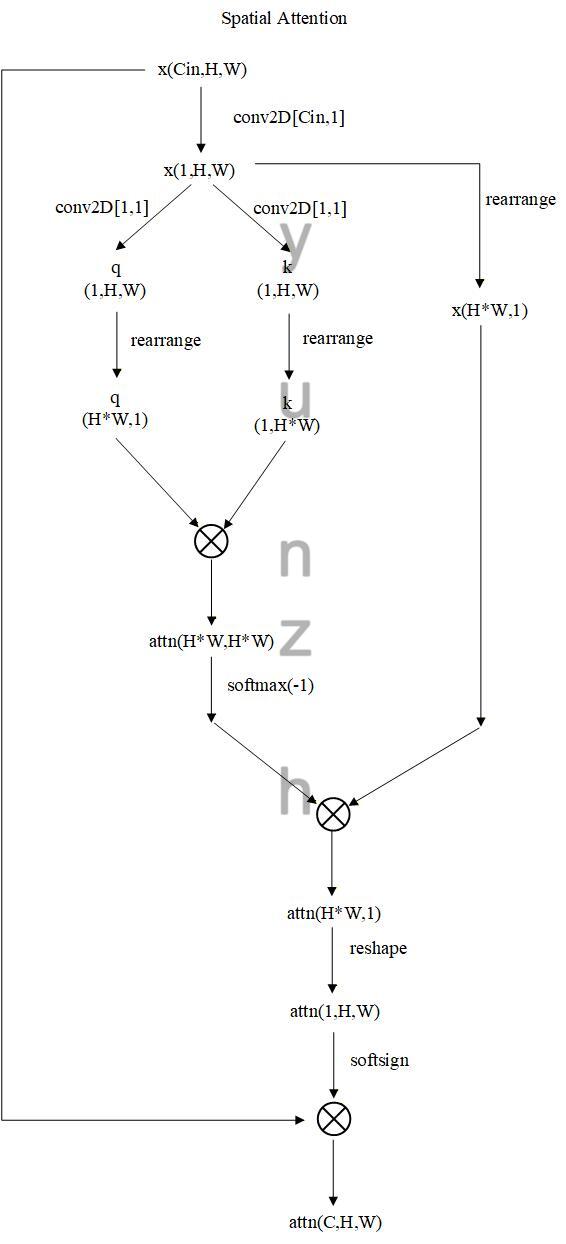
2.3 解码器中的上采样模块(Up)
开源项目中双Unet的解码器由4个上采样模块(Up)组成,上采样模块的结构如下图所示:
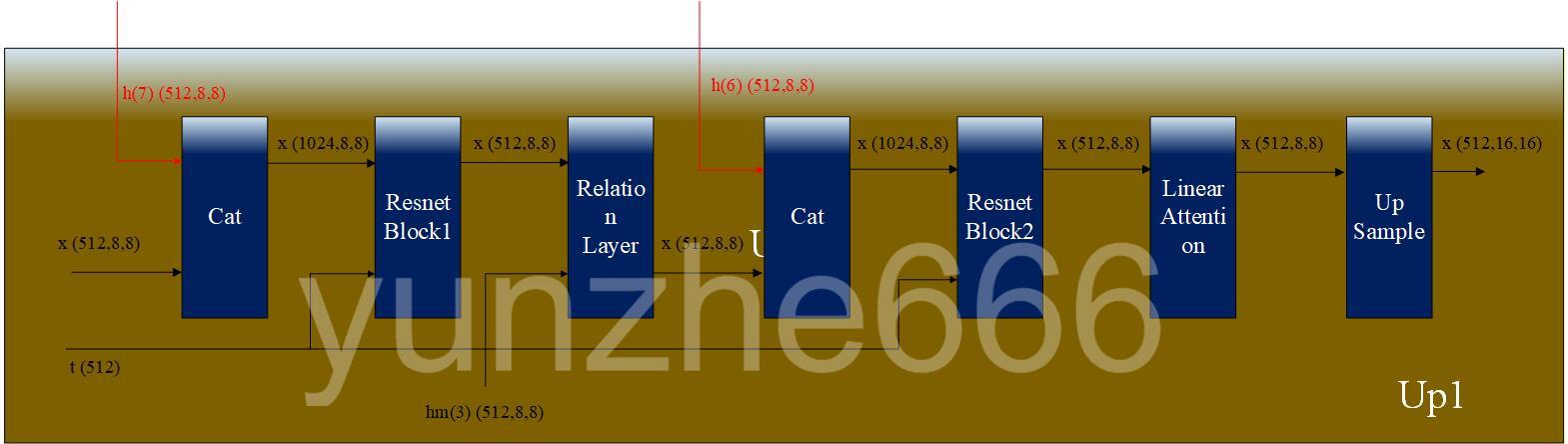
其中Upsample由nn.upsample和nn.conv2D组成。其余的Resnet Block、Relation layer、linear attention前面均已介绍。
至此双Unet的整个网络结构也已介绍完毕。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号