搜索二叉树删除节点和修减二叉树

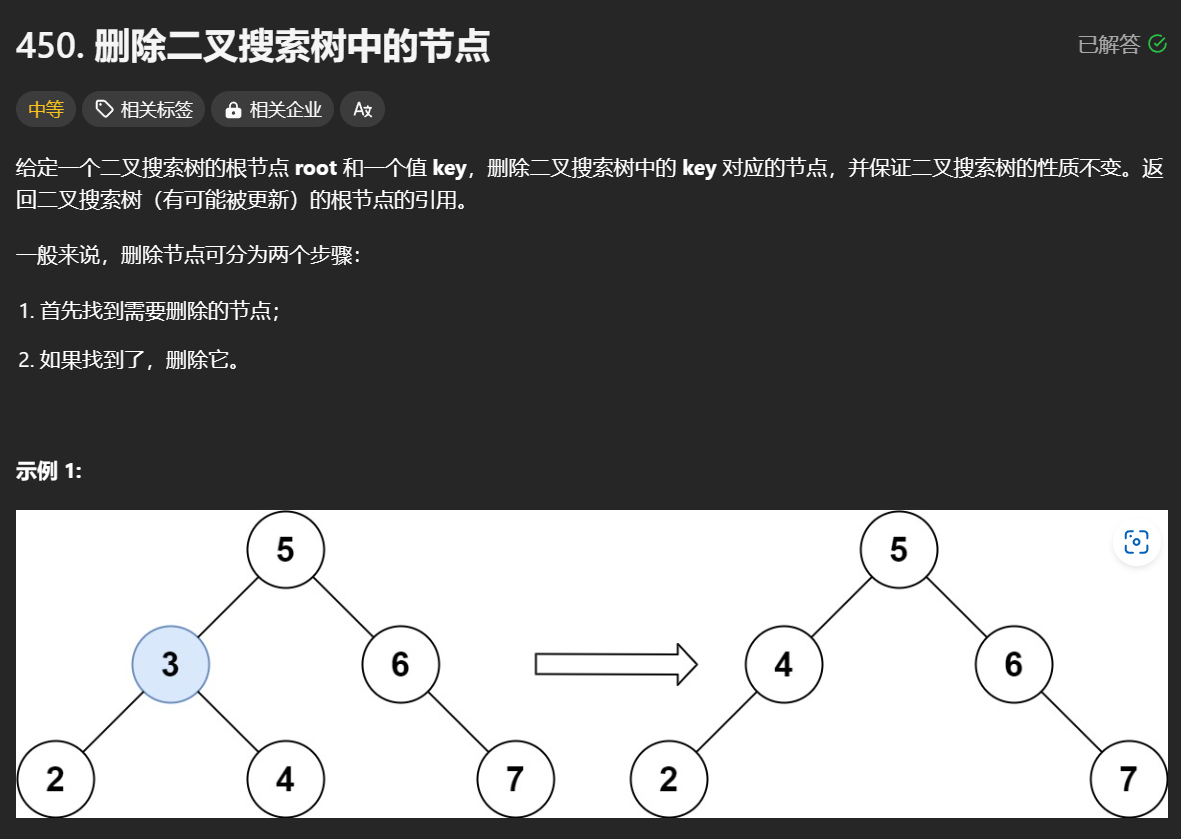
删除目标节点首先要找到该节点，因此用到搜索二叉树的性质去寻找，该节点比target大就看左子树部分，小就看右子树部分。
根据主函数可知，最后是返回一个节点，也可以看成是返回一个子树。因此查找的时候就要承接这子树，这子树就是删除好后的结果。

点击查看代码

if(!root){return NULL;}
if(root->val>key){root->left=deleteNode(root->left,key);}
else if(root->val<key){root->right=deleteNode(root->right,key);}

删除部分是关键，根据左右子树的是否为空，可以分为几种情况， 较为复杂的就是都不为空的情况，这时候要找到右子树中最小的点，再将左子树接上去。

点击查看代码

class Solution {
public:
TreeNode*findmin(TreeNode*root){
    while(root->left){
        root=root->left;
    }
    return root;
}
    TreeNode* deleteNode(TreeNode* root, int key) {
if(!root){return NULL;}
if(root->val>key){root->left=deleteNode(root->left,key);}
else if(root->val<key){root->right=deleteNode(root->right,key);}
else{
    if(!root->left&&!root->right){return NULL;}
    else if(!root->left&&root->right){
        return root->right;
    }
    else if(root->left&&!root->right){
        return root->left;
    }
    else{
TreeNode*place=findmin(root->right);
place->left=root->left;
return root->right;
    }
}
return root;
    }
};

修建二叉树看起来了要比删除树要复杂，因为他有多个节点要删除嘛。
但是实际代码要简单很多，这道题相当与重新构造一棵二叉搜索树，把符合条件的点都添加进来。
根据二叉搜索树的特性，把在范围外的子树都可以排除不仅仅是节点。

点击查看代码

if(root->val<low){return trimBST(root->right,low,high);}
if(root->val>high){return trimBST(root->left,low,high);}

同样是需要承接已经构造好的左右子树。 root->left=trimBST(root->left,low,high); root->right=trimBST(root->right,low,high);

完整代码

点击查看代码

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root){return NULL;}
if(root->val<low){return trimBST(root->right,low,high);}
if(root->val>high){return trimBST(root->left,low,high);}
root->left=trimBST(root->left,low,high);
root->right=trimBST(root->right,low,high);
return root;
    }
};