回溯过程浅理解

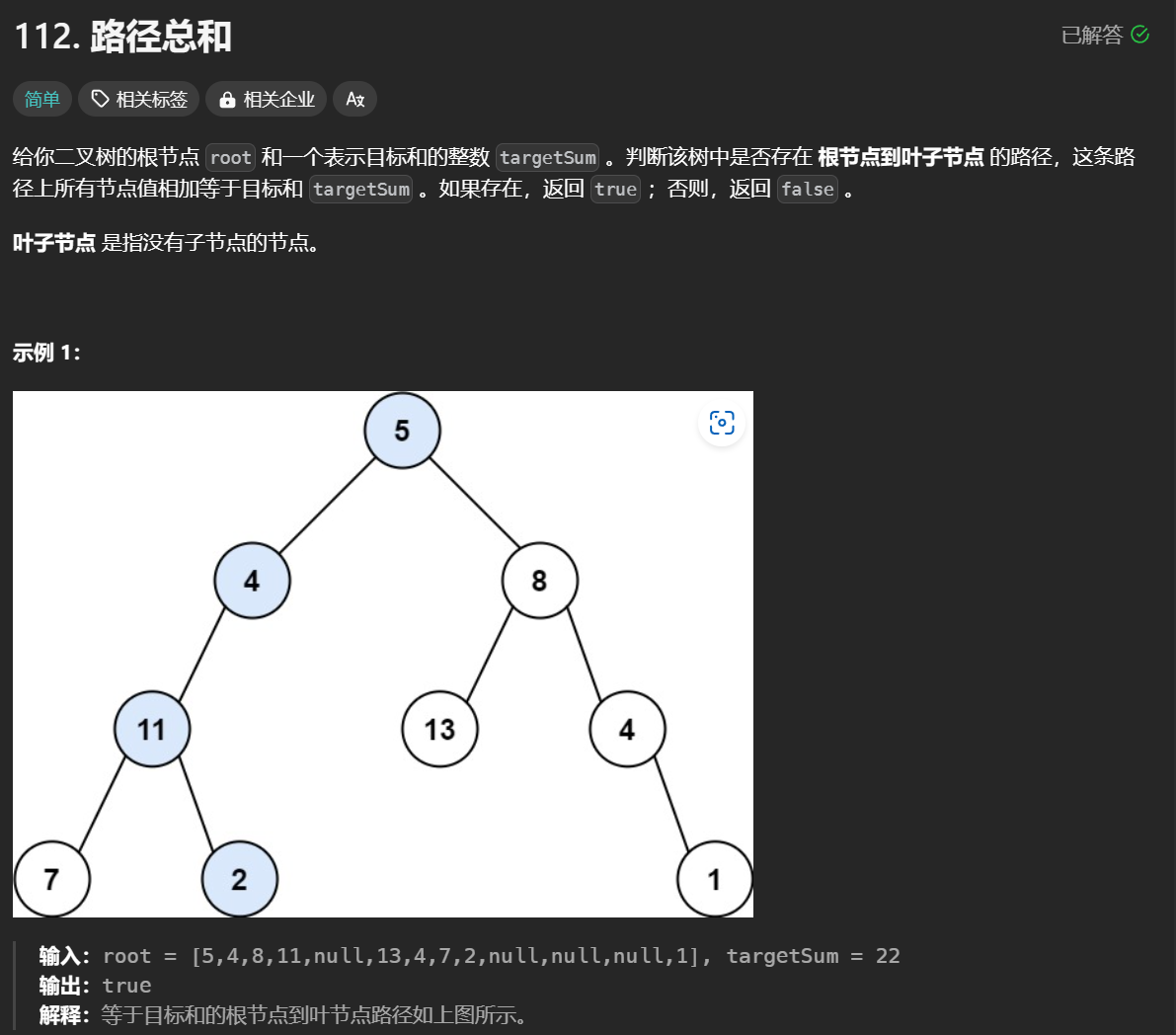
如何知道这一题需要用回溯呢？
回溯就像试触，如果不符合条件，就往回缩，但是这种缩，不是回到起点，而是回到上一步。
所以题目像二叉树路径，这样需要不断的试触并且要记录之前的路径信息的，就要用到回溯。

关于回溯如何用，有一些关键点。
有递归就有回溯，
单层递归中有加就有减，（这个加减要广义的理解，加就是向下遍历，减就是回退）
递归传递写中间。

点击查看代码

if (cur->left) { // 左
    count -= cur->left->val; 
    if (traversal(cur->left, count)) return true;
    count += cur->left->val;
}

这个代码就相当于

点击查看代码

if (cur->left) { // 左 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    if (traversal(cur->left, count - cur->left->val)) return true; // 注意这里有回溯的逻辑
}

一个意思，只不过隐藏了回溯过程。

回到题目本身，最开始写的时候是遍历一个节点，就将其值插入数组中，到叶子节点的时候再做判断。

点击查看代码

class Solution {
public:
void path(TreeNode*root,vector<int>&v,vector<int>&cnt){
if(root){v.push_back(root->val);}
if(!root->left&&!root->right){
    int sum=0;
    for(int i=0;i<v.size();i++){
        sum+=v[i];
    }
    cnt.push_back(sum);
   
}
if(root->left){
path(root->left,v,cnt);
v.pop_back();
}
if(root->right){
    path(root->right,v,cnt);
    v.pop_back();
}

}
    bool hasPathSum(TreeNode* root, int targetSum) {
        vector<int>v,cnt;
        if(!root){return false;}
path(root,v,cnt);
for(int i=0;i<cnt.size();i++){
    if(targetSum==cnt[i]){return true;}
}
return false;
    }
};

看了卡哥的方法，他是向下遍历时，减去该节点的值，如果到叶子节点时，count等于0，就代表找到一条路径。

点击查看代码

class Solution {
private:
    bool traversal(TreeNode* cur, int count) {
        if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
        if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回

        if (cur->left) { // 左
            count -= cur->left->val; // 递归，处理节点;
            if (traversal(cur->left, count)) return true;
            count += cur->left->val; // 回溯，撤销处理结果
        }
        if (cur->right) { // 右
            count -= cur->right->val; // 递归，处理节点;
            if (traversal(cur->right, count)) return true;
            count += cur->right->val; // 回溯，撤销处理结果
        }
        return false;
    }

public:
    bool hasPathSum(TreeNode* root, int sum) {
        if (root == NULL) return false;
        return traversal(root, sum - root->val);
    }
};