11--中缀表达式转后缀表达式

思路步骤分析：

1、初始化两个栈，运算符栈s1和储存中间结果的栈s2

2、从左至右扫描中缀表达式

3、遇到操作数时，将其压入s2

4、遇到运算符时，比较其与s1z栈顶运算符的优先级：

4.1：如果s1为空，或栈顶运算符为左括号“(”,则直接将此运算符入栈

4.2：否则，若优先级比栈顶运算符高，也将运算符压入s1

4.3：否则，将s1栈顶的运算符弹出并压入到s2中，再次转到（4.1）与新的栈顶运算符比较；

5、遇到括号时：

5.1：遇到左括号"("，则直接压入s1

5.2：如果是右括号")",则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

6、重复步骤2至5，直到表达式的最右边

7、将s1中剩余的运算符依次弹出并压入s2

8、依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

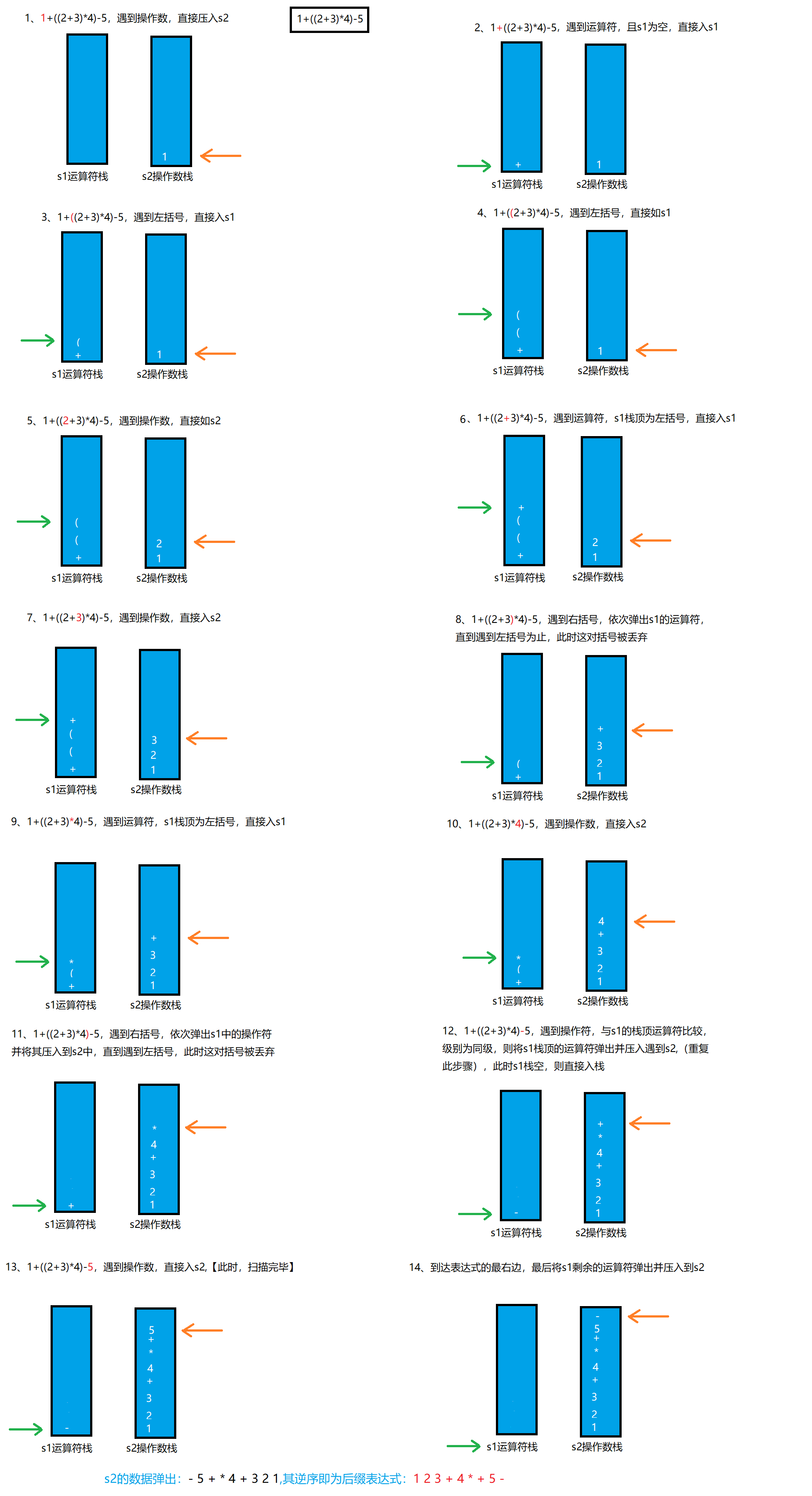
中缀表达式1+((2+3)*4)-5，图形过程：

//新定义一个类【工具类】，用于比较运算符优先级
class Operator{
    public static final int  ADD = 1;
    public static final int  SUB = 1;
    public static final int  MUL = 2;
    public static final int  DIV = 2;
    
    public static int priority(String item) {
        int ret = 0;
        switch(item) {
        case "+":
            ret = ADD;
            break;
        case "-":
            ret = SUB;
            break;
        case "*":
            ret = MUL;
            break;
        case "/":
            ret = DIV;
            break;
        default:
            break;
        }
        return ret;
    }
}

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

//逆波兰表达式的计算
public class NiPolandExpression {

    public static void main(String[] args) {
        String expression = "1+((2+3)*425)-15"; //2111
        List<String> list = toInfixListExpression(expression);
        System.out.println(list);
        
        List<String> lists =  parseSuffixExpression(list);
        System.out.println(lists);
        
        //1、将表达式转成ArrayList集合，后遍历，每遍历一个元素将压栈
        Stack<String> stack = new Stack<>();
        for(String ele: lists) {
            if (ele.matches("\\d+")) { //正则表达式：表示匹配一个或者多个整数
                //是数字直接入栈
                stack.push(ele);
            }else {
                //到了这里说明是符号,需要pop出2个操作数
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int ret = 0;
                switch(ele) {
                case "+": 
                    ret = num1 + num2;
                    break;
                case "-":
                    ret = num1 - num2;
                    break;
                case "*":
                    ret = num1 * num2;
                    break;
                case "/":
                    ret = num1 / num2;
                    break;
                    }
                //将计算结果压入栈中
                stack.push(ret+"");
            }
        }
        int result = Integer.parseInt(stack.pop());
        System.out.println("最终结果为：" + result);
    }
    
    public static List<String> getList(String expression){
        List<String> lists = new ArrayList<>();
        String[] arrays = expression.split(" ");
        for(String ele:arrays) {
            lists.add(ele);
        }
        return lists;
     }
    
    //将中缀表达式转成List集合
    public static List<String> toInfixListExpression(String expression){
        List<String> lists = new ArrayList<>();
        int i = 0; //字符串每个字符的索引
        char ch = ' ';
        while(i < expression.length()) {
            ch = expression.charAt(i);
            if (ch < '0' || ch > '9') {
                //说明为运算符，直接加入到lists集合中
                lists.add(ch+"");
                i++;
            }else {
                //说明改字符为数字
                String str = "";
                while(i < expression.length() && expression.charAt(i) >= '0' && expression.charAt(i) <= '9') {
                    str += expression.charAt(i++);
                }
                lists.add(str);
            }
        }
        return lists;
    }
    
    //中缀表达式转后缀表达式
    public static List<String> parseSuffixExpression(List<String> lists){
        //定义运算符栈
        Stack<String> s1 = new Stack<>();
        //定义存储中间结果的栈s2 【由于在转换过程中s2只添加数据，因此可以使用集合】
        //Stack<String> s2 = new Stack<>();
        List<String> s2 = new ArrayList<>();
        //扫描中缀表达式【集合】
        for(String item : lists){
            //如果是操作数，直接加入到s2中
            if (item.matches("\\d+")) {
                s2.add(item);
            }else if ("(".equals(item)) {
                //如果是左括号，直接压入s1
                s1.push(item);
            }else if(")".equals(item)){
                //依次弹出s1栈顶的运算符，并压入s2,直到遇到左括号为止，将这对括号丢弃
                while(!"(".equals(s1.peek())) {
                    s2.add(s1.pop());
                }
                //弹出s1中的左括号
                s1.pop();
            }else {
                //遇到运算符
                //当item的优先级小于或者等于s1栈顶的优先级时，则依次将s1栈顶的运算符pop到s2中，再次与s1新的栈顶的运算符相比较
                //直到当前运算符的优先级大于s1栈顶运算符的优先级
                //注：如果s2.peek为"("则返回0，会直接跳出循环
                while(s1.size() != 0 && Operator.priority(item) <= Operator.priority(s1.peek())) {
                    s2.add(s1.pop());
                }
                //到达此处说明有3种【直接入栈s1】情况：
                  //1、item运算符的优先级大于s1栈顶运算符的优先级
                  //2、s1为空
                  //3、s1栈顶为左括号
                s1.push(item);
            }
        }
        //将s1中剩余的运算符弹出并加入到s2中
        while(s1.size() != 0) {
            s2.add(s1.pop());
        }
        return s2;
    }
    
}