尾递归

递归，我们大家都会吧，但是有一种叫做尾递归的，了解吗？本文主要讲解一下尾递归的事儿。

一、引入

编程题：输入一个整数n，输出斐波那契数列的第n项

 给你来个简单点儿的例子，计算n的阶乘

二、递归实现

function fibonacci(n) {
  if (n === 0 || n === 1) {
    return n;
  }
  return fibonacci(n - 1) + fibonacci(n - 2);
}

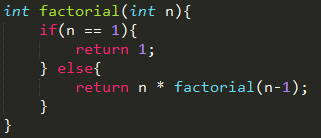
 三、普通递归的问题：

上面的递归实现，是确实能解决问题的，毫无疑问！但是，当我们在测试的时候，用一个较大的数字，百日fibonacci（50）fibonacci（10000）...,你会发现运行要等待很久。如果数字再大一点，还会出现堆栈异常，为什么会很慢，堆栈异常呢。关于原理，请参考

张大胖学递归一文。此文详细讲解了递归对栈的使用原理。简单来说，就是数字太多，递归的栈存储空间会很大，大量的入栈，出栈，等等会消耗很多时间。同时栈不可能无限大。当n较大到超过栈空间的容量大小，就会产生异常。如下

 

四、尾调用

 在解决上面问题之前，先来了解一下什么是尾调用。

尾调用：一个函数里的最后一个动作是返回一个函数的调用结果，即最后一步新调用的返回值被当前函数返回

比如：

function f(x) {
  return g(x)
}

 

下面这些情况不属于尾调用：

function f(x) {
return g(x) + 1 // 先执行g(x)，最后返回g(x)的返回值+1
}

function f(x) {
let ret = g(x) // 先执行了g(x)
return ret // 最后返回g(x)的返回值
}

五、尾递归

如果函数在尾调用位置调用自身，则称这种情况为尾递归。尾递归是一种特殊的尾调用，即在尾部直接调用自身的递归函数

由于尾调用消除，使得尾递归只存在一个栈帧，所以永远不会“爆栈”。

尾递归改写上面的递归：

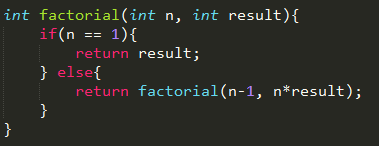
factorial(6, 1) 

 

// 修改后
'use strict'
function fibonacci(n, pre, cur) {
  if (n === 0) {
    return n;
  }
  if (n === 1) {
    return cur;
  }
  return fibonacci(n - 1, cur, pre + cur);
}
// 调用
fibonacci(6, 0, 1)

关于尾递归，尾调用，参考面试官：用“尾递归”优化斐波那契函数一文

尾递归改写后，测试n=10000，秒算。但是用传统递归，可能要几十分钟，几个小时等

事实上，可以测试，当n=100 000 000以上时，在java中用尾递归也会出现StackOverflowError，但是在scala编译器中，此处却可以无限大。当数量级达到这个程度时，不能用栈，而需要改用动态规划dp算法来解决。

static long fib4(int N) {
        if (N == 0) return 0;
        long dp[] = new long[N+1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= N; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[N];
    }
如上代码，dp算法不需要用到大量栈，但是用到了堆内存。一般堆内存相较于栈空间大得多。所以不会出现栈异常，也暂时不会出现堆内存异常等

 

细心的读者会发现，根据斐波那契数列的状态转移方程，当前状态 n 只和之前的 n-1, n-2 两个状态有关，其实并不需要那么长的一个 DP table 来存储所有的状态，只要想办法存储之前的两个状态就行了。

所以，可以进一步优化，把空间复杂度降为 O(1)。这也就是我们最常见的计算斐波那契数的算法：

static long fibonacci(int n) {
        long cur = 0;
        long next = 1;
        for (int i = 0; i < n; i++) {
            long temp = cur;
            cur = next;
            next += temp;
        }
        return cur;
    }

 在scala语言中，通过对尾递归和地推两类算法比较如下：

当N较小时，两者差异不大，地推运算小幅略胜。当N比较大时，就很明显，尾递归优势更明显。

object Main {
  def main(args: Array[String]): Unit = {
    println("Hello world!")
    val startTime = System.currentTimeMillis();
    val N = 900000000L;
    println(fib(N, 0 ,1))
    val endTime = System.currentTimeMillis();
    println("尾递归用时：",endTime -startTime)
    println(fib2(N))
    val endTime2 = System.currentTimeMillis();
    println("递推用时：",endTime2 -endTime)

  }

  def fib(n: Long, pre:Long, cur: Long):Long = {
    if (n == 0) {
      return n;
    }
    if (n == 1) {
      return cur;
    }
    return fib(n-1, cur, cur + pre)
  }

  def fib2(n: Long): Long = {
    var cur = 0;
    var next = 1;
    var count = 0;
    while( count <= n ) {
        count = count +1;
        var tmp = cur;
        cur = next;
        next = next + tmp
    }
    return cur;
  }
}

打印结果
Hello world!
-2694463113204044800
(尾递归用时：,496)
788805121
(递推用时：,536)

当N再添加一个0时，发现尾递归用时呈指数增长。而尾递归大约增长10倍。综合，scala中建议使用尾递归。