Leetcode:516. Longest Palindromic Subsequence

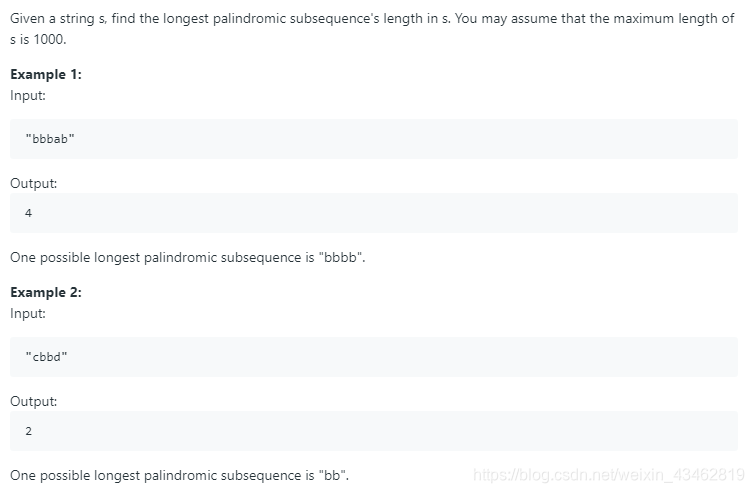
求最长回文子序列的长度。
方法一：
复制字符串并倒序，求两个字符串的最长公共子序列：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        if (s.empty())
            return 0;
        string& s1 = s;
        string s2 = s;
        reverse(s2.begin(), s2.end());
        int sz = s.size();
        vector<vector<int>> dp(sz, vector<int>(sz, 0));
        if (s1[0] == s2[0])
            dp[0][0] = 1;
        for (int i = 1; i < sz; ++i)
            dp[i][0] = (s1[i] == s2[0] ? 1 : dp[i-1][0]);
        for (int j = 1; j < sz; ++j)
            dp[0][j] = (s1[0] == s2[j] ? 1 : dp[0][j-1]);
        for (int i = 1; i < sz; ++i)
            for (int j = 1; j < sz; ++j) {
                if (s1[i] == s2[j])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else 
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        return dp.back().back();
    }
};

方法二：
dp[i][j]: s:i->j最长回文子序列长度
if s[i] == s[j]: dp[i][j] = dp[i+1][j-1] + 2
else dp[i][j] = max(dp[i+1][j], dp[i][j-1])

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int sz = s.size();
        if (sz == 0)
            return 0;
        vector<vector<int>> dp(sz, vector<int>(sz, 0));
        for (int i = sz-1; i >= 0; --i) 
            for (int j = i; j < sz; ++j) {
                if (i == j) {
                    dp[i][j] = 1;
                    continue;
                }
                if (s[i] == s[j])
                    dp[i][j] = dp[i+1][j-1] + 2;
                else
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
            }
        return dp[0].back();
    }
};