LeetCode：437. Path Sum III

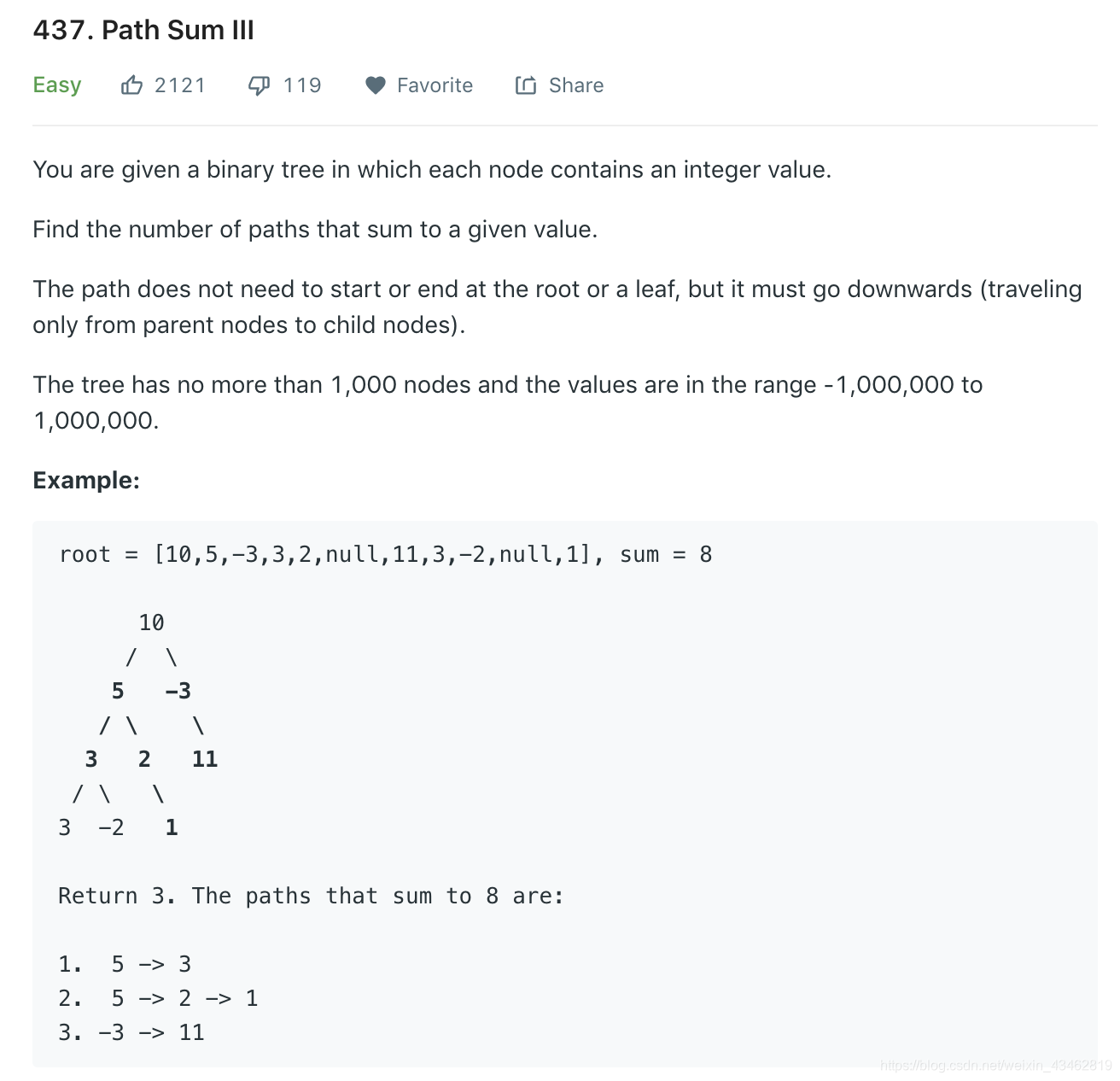
这题应该不算太难，但是有一个比较有意思的解法。

解法一：前缀和。
最近做了不少前缀和的题目，看到这问题的第一反应就是前缀和。但是写的时候还是出了很多问题：
啊树也可以前缀和。不仅一维数组，二维数组可以前缀和，树也可以前缀和啊～

class Solution {
public:
    int pathSum(TreeNode* root, int sum) {
        if (!root)
            return 0;
        unordered_map<int, int> preSum;
        preSum[0] = 1;//别忘了这个
        int retCnt = 0;
        helper(root, sum, 0, preSum, retCnt);
        return retCnt;
    }
private:
    void helper(TreeNode* node, int targetSum, int tempSum, unordered_map<int, int>& preSum, int& retCnt) {
        if (!node)
            return;
        tempSum += node->val;
        retCnt += preSum[tempSum - targetSum];//找的是在当前节点之前的前缀和为tempSum - targetSum的节点
        preSum[tempSum]++;//所以这一行得放在后面
        helper(node->left, targetSum, tempSum, preSum, retCnt);
        helper(node->right, targetSum, tempSum, preSum, retCnt);
        preSum[tempSum]--;
    }
};

注意其中的注释。因为是想找在这个位置前面的符合条件的节点，如果在找之前就把当前节点的前缀和放进去了，那么如果想要找的是和为0的，那么就会多算上当前的这个，这显然是不行的。

方法二：
有意思的来了：

class Solution {
public:
    int pathSum(TreeNode* root, int sum) {
        if (!root)
            return 0;
        return pathSumFrom(root, sum, 0) + pathSum(root->left, sum) + pathSum(root->right, sum);
    }
private:
    int pathSumFrom(TreeNode* node, int targetSum, int tempSum) {
        if (!node)
            return 0;
        tempSum += node->val;
        return (tempSum == targetSum ? 1 : 0) + pathSumFrom(node->left, targetSum, tempSum) + pathSumFrom(node->right, targetSum, tempSum);
    }
};
//相当神奇的解法，两个递归，有点难以理解
//其实就是：在每个节点处，计算以它为开始的所有路径中符合条件的个数。
//这种解法其实简单，但是这种需要多次遍历的方法在潜意识中就把它排除了。相对来说，前缀和的方法还是效率高一些的

这个解法有点意思的，两个递归。
但是效率会低一些，遍历很多遍树。所以只是写法简洁而已。

另外，在这题的评论区看到有位老铁说的话说到我心缝里面了：写递归的技巧是：明白一个函数的作用并相信它能完成这个任务，千万不要跳进这个函数里面企图探究更多细节，否则就会陷入无穷的细节无法自拔。
这也是我写递归的时候一直告诉自己的：就算当前这个函数我还没有完成，但是我是可以调用它自身的，并且我相信他能够完成任务。